George Dodwell était l’astronome du gouvernement de l’Australie-Méridionale. À sa mort en 1963, la Société astronomique d’Australie-Méridionale demanda à Barry Setterfield de préparer les notes de Dodwell pour la publication. C’est ce que Barry a fait. Cependant, il n’a pas réussi à trouver un éditeur en Australie pour les œuvres de Dodwell.
Un de ses amis a proposé de prendre le matériel et de le faire publier sous les auspices d’une université aux États-Unis. C’était à la fin des années 1980. On nous a parlé d’un certain nombre de difficultés différentes au fil des ans qui ont retardé la publication, mais la publication n’a toujours pas eu lieu. Récemment, nous avons reçu des fichiers de ce que cette personne avait préparé et nous avons découvert qu’elle avait fait un certain nombre d’erreurs de frappe et, à deux moments au moins, qu’elle avait inséré ses propres phrases qui n’étaient pas dans le texte original et qu’elle ne les avait pas marquées comme distinctes du texte original. Ce n’est pas acceptable.
Entre-temps, les fils de Dodwell devenaient également un peu impatients, et à leur demande et avec leur permission, le matériel sur l’obliquité de l’écliptique (l’inclinaison de l’axe de la terre) est maintenant présenté ici dans son intégralité pour la première fois.
Comme nous avons nous-mêmes les manuscrits originaux, chaque mot a été vérifié et chaque signe de ponctuation pour en assurer l’exactitude. Nous avons occasionnellement modifié certains paragraphes et ponctuations pour améliorer la lisibilité (Dodwell aimait beaucoup les virgules), et avons inséré des tableaux formels à la place des tableaux informels dans le manuscrit original. Les figurines ont été numérisées à partir des originaux et dimensionnées aussi grandes que possible pour permettre la lecture, même en petits caractères. Le seul problème majeur que nous avons rencontré était un schéma manquant du temple de Tiahuanaco (chapitre 10) auquel Dodwell fait référence dans le dernier chapitre.
Tous les accents sont dans l’original.
Voici, enfin, le travail de Dodwell. Nous tenons à exprimer nos sincères remerciements à David Bowdoin pour les heures de travail qu’il a consacrées à nous aider à préparer les vieilles photographies, les tableaux et les diagrammes de Dodwell et à les mettre ici dans le manuscrit. Nous sommes également très reconnaissants à John et Peter Dodwell de leur aide pour localiser les photographies sur la page des photos, de leur aide pour les légendes et de leurs encouragements tout au long de ce processus. Nous avons ajouté un certain nombre d’autres images en plus des originaux de Dodwell qui, selon nous, aident le lecteur à comprendre ce qui est écrit.
Cordialement,
Barry et Helen Setterfield,
23 février 2010
À propos de George Dodwell (1879
- 1963)
par Barry Setterfield
George Frederick Dodwell est né à Leighton Buzzard, en Angleterre, le 13 février 1879. Après avoir déménagé en Australie, Dodwell a obtenu son diplôme à l’Université d’Adélaïde et est devenu membre de la Royal Astronomical Society. Il est nommé au personnel de l’Observatoire d’Adélaïde le 1er mars 1899, en tant que calculateur junior (la personne responsable des calculs mathématiques) sous Sir Charles Todd qui avait lui-même été formé par Sir George Airy à l’Observatoire royal de Greenwich. Il succéda à Sir Charles, étant nommé astronome du gouvernement pour l’Australie-Méridionale en juin 1909. Dodwell occupa ce poste jusqu’à sa retraite le 31 octobre 1952.
Pendant son séjour à l’Observatoire d’Adélaïde, il a eu de nombreuses réalisations à son actif, à propos desquelles il était généralement humble. En 1900, peu de temps après l’invention de la télégraphie sans fil, l’Observatoire est devenu le site de la première installation sans fil en Australie pour la signalisation à distance. L’occasion s’est présentée de fixer la frontière entre l’Australie-Méridionale et l’Australie-Occidentale, qui a été définie comme le 129e méridien à l’est de Greenwich. C’est George Dodwell lui-même qui a proposé que cela soit déterminé par les signaux sans fil entendus par Greenwich ainsi que par les stations de terrain de Deakin et d’Argyle Downs simultanément. Les signaux horaires radio étaient transmis de Bordeaux, Lyon et Annapolis. Ce projet international relie les observatoires de Greenwich, Paris et Washington ainsi que ceux d’Australie d’avril à juillet 1921. C’était la première fois que le monde était mesuré d’un côté à l’autre par la télégraphie sans fil en conjonction avec l’observation astronomique. Il s’agit d’une « première mondiale » pour Adélaïde et George Dodwell.
D’autres travaux qui ont valu à l’Observatoire d’Adélaïde une reconnaissance mondiale sous la direction de George Dodwell comprenaient une étude magnétique de l’Australie-Méridionale. Cela l’a conduit à étudier les variations de latitude en collaboration avec l’observatoire de La Plata en Argentine, le Congrès international de la latitude et l’Association astronomique internationale. En septembre 1922, il dirigea un groupe combiné avec Sir Kerr Grant de l’Université d’Adélaïde pour observer et photographier l’éclipse solaire totale de Cordillo Downs, en Australie, afin de tester la théorie d’Einstein sur l’effet de la gravitation sur la lumière. La même année, il est nommé par le Commonwealth d’Australie pour être son représentant à la conférence astronomique internationale de Rome.
L’étude des variations de latitude a conduit George Dodwell à étudier l’obliquité de l’écliptique (l’inclinaison de l’axe de la terre). Ce travail a commencé en 1934, un an après que son oncle, Sir Frank Dyson, K.B.E., F.R.S., ait pris sa retraite en tant qu’astronome royal en Angleterre. Un manuscrit ancien d’un astronome belge médiéval Godefroid Wendelin, contenant des observations de l’Obliquité, a été publié en 1933 et a été obtenu par Dodwell. L’ensemble des données a révélé une anomalie progressive et unilatérale par rapport à la formule de Newcomb. En 1935, Dodwell envoya un article préliminaire à la Royal Astronomical Society. Les arbitres ont suggéré une étude plus approfondie des erreurs d’observation. Cela a été entrepris à titre expérimental à l’Université d’Adélaïde en juin 1936 avec neuf expérimentateurs effectuant 172 observations sur un gnomon vertical. Un premier rapport couvrant la période de décembre 1934 à décembre 1936 a été présenté au Parlement d’Australie-Méridionale le 20 février 1937. À cette occasion, Dodwell annonça qu’un compte rendu était en préparation pour publication. Il souhaitait que cette recherche soit publiée sous la forme d’un rapport de l’Observatoire d’Adélaïde. Cependant, l’Observatoire a été fermé en 1952 à sa retraite. Ses recherches sur le sujet se sont poursuivies, mais le rapport n’a été achevé que juste avant sa mort le 10 août 1963.
Ce qui suit est le manuscrit de ses recherches.
*********************************
Note : George Dodwell a écrit deux sections dans son manuscrit. La première concernait l’exposition biblique. Le second avec le matériel astronomique. Ses recherches astronomiques sont venues en premier et son application biblique plus tard dans sa vie. Cette préface était pour les deux sections et comme nous ne mettons que le matériel astronomique sur notre site Web, nous avons inséré des ellipses dans sa préface où nous avons supprimé les références à son matériel biblique. Cette préface est le seul endroit où son matériel original a été édité.
Barry et Helen Setterfield
En 1934, j’avais un grand désir de faire un travail particulier qui pourrait être d’une valeur en astronomie et aussi d’un intérêt général. … [Plus tard], en parcourant la bibliothèque de l’observatoire d’Adélaïde, mon attention a été éveillée par un livre intitulé « Draysonia », écrit par l’amiral britannique Sir Algernon F. R. DeHorsey. Il se référait à une théorie astronomique avancée par le major-général Alfred Wilks Drayson, qui avait été pendant 15 ans professeur à l’Académie militaire royale de Woolwich, et également astronome à l’Observatoire royal de Greenwich. L’amiral DeHorsey avait été l’un de ses élèves à Woolwich et avait une grande appréciation de son travail.
Le livre donnait une explication de ce que le professeur Drayson croyait être un mouvement de la terre, en plus des mouvements déjà connus, et se déroulait autour de ce qu’il appelait un « deuxième pôle de précession ». * Il a affirmé que ce mouvement expliquait les climats géologiques passés de la terre et les périodes glaciaires.
Je savais que la théorie du professeur Drayson était considérée comme un paradoxe, contraire à la saine doctrine astronomique, par les hautes autorités astronomiques ; et je voulais savoir où il était dans l’erreur. Il devint bientôt clair que le paradoxe résidait dans le fait que pour ce mouvement physique et cyclique proposé de la terre, qu’il croyait toujours en cours, il n’y avait apparemment aucune cause physique connue ou possible.
Néanmoins, bien que la théorie fût ainsi insoutenable, il m’a semblé utile de retracer plus clairement dans quelle mesure et pourquoi les observations anciennes et médiévales de l’obliquité de l’écliptique, sur lesquelles le professeur Drayson fondait ses conclusions, différaient de la formule internationalement acceptée de Newcomb pour la variation séculaire, ou séculaire, de l’obliquité. Ces observations remontent aux valeurs données par Strabon, Proclus, Ptolémée et Pappus dans les premiers siècles de l’ère chrétienne. Ils ont indiqué une divergence constante et croissante dans les âges passés par rapport aux valeurs calculées au moyen de la formule de Newcomb.
Sir George Airy, le septième astronome royal d’Angleterre, a affirmé il y a longtemps le principe, dans son livre sur la théorie des erreurs, que dans les recherches astronomiques et autres recherches statistiques, aucune observation, même apparemment imparfaite ou peu fiable en elle-même, ne doit être rejetée, mais toutes les observations, après correction pour les sources d’erreur connues, doivent être utilisées pour former le résultat moyen ou moyen. car dans une longue série, les valeurs très élevées auraient tendance à être contrebalancées par les valeurs très faibles.
La validité de ce principe est illustrée par une illustration, signalée par A.R. Wallace, que la taille moyenne du plus grand géant et du plus petit nain de la Grande-Bretagne est presque exactement la même que la taille moyenne de l’ensemble de la population.
On le voit également dans le tir à la cible, où, avec un grand nombre de tirs, la position moyenne entre les tirs très hauts et très bas, ainsi que les tirs très larges des deux côtés de la cible, se trouve être très proche du centre de la cible.
Le principe correct, donc, dans l’étude des observations médiévales et anciennes de l’obliquité de l’écliptique, devrait être, premièrement, d’obtenir autant de ces observations que possible ; deuxièmement, corriger chacune d’elles, dans la mesure du possible, pour toute source d’erreur connue ou vérifiable ; et ensuite de tracer la courbe qui les unit tous les uns aux autres et aux observations modernes. Alors, d’après le caractère mathématique de la courbe, nous pouvons peut-être trouver une vérité ou une circonstance nouvelle, révélée par les observations, et jusqu’alors insoupçonnée.
Tel était donc le plan que je m’efforçais de suivre. J’ai donc écrit, et cherché dans de nombreux livres, ce genre d’informations de la Chine ancienne, de l’Inde, de l’Égypte et de la Grèce, ainsi que de l’Europe médiévale et de certaines parties de l’Asie. Les résultats sont donnés dans les chapitres 3 à 10 de ce volume, Recherches astronomiques sur l’obliquité de l’écliptique. [note : c’était son titre initial qu’il a lui-même changé par la suite]
Au début, j’ai eu la chance d’obtenir une copie du premier manuscrit du célèbre astronome belge médiéval, Godefroid Wendelin, qui avait été perdu pendant trois siècles, jusqu’à ce qu’il soit récemment découvert dans la bibliothèque de la ville de Bruges. Il a été publié en 1933 par M. l’abbé G. Lemaître, dans le vol. 9. 1932 des Publications du Laboratoire d’Astronomie et de Géodésie de l’Université de Louvain.
Cet ouvrage contenait, entre autres choses, une liste d’anciennes observations de l’obliquité de l’écliptique, faites par Thalès, vers 558 av. J.-C. ; Ératosthène, vers 230 av. J.-C. ; dans ses dernières années, Hipparque, 135 av. J.-C. ; Ptolémée, 126 apr. J.-C. ; et par plusieurs astronomes médiévaux jusqu’à l’époque de Tycho Brahe, 1587 ap. J.-C., et de Wendelin lui-même, 1616 ap. J.-C. ; ainsi que la théorie de Wendelin sur la cause du changement qui s’était produit au cours des âges jusqu’à son époque.
Mes recherches ultérieures sur les observations anciennes et médiévales de l’obliquité de l’écliptique ont abouti à rassembler et à analyser une série très considérable et précieuse de ces observations.
La première courbe de ces anciennes observations, que j’ai dessinée en 1934, montrait une anomalie indubitable et progressive par rapport à la formule de Newcomb. Une étude attentive des observations, et de leur concordance avec la courbe en tout temps et en tous lieux d’observation, a montré que cela n’était pas dû à de grandes erreurs dans les observations anciennes. C’était donc très déroutant, car cela semblait indiquer un mouvement inconnu de la terre dans le passé. Il ne pourrait pas s’agir d’un mouvement périodique cyclique ou continu, car une telle explication ne ferait que répéter le paradoxe draysonien et serait impossible.
… Après avoir
tracé initialement la courbe, en unissant toutes les observations alors
disponibles, j’ai tracé une courbe subsidiaire des « résidus », c’est-à-dire des
différences trouvées en soustrayant les quantités calculées par la formule de
Newcomb de celles données par les observations. Puisque la formule de Newcomb
représente complètement toutes les forces connues régissant le mouvement lent et
régulier de l’axe de la terre, une courbe de résidus tendrait à indiquer une
condition inconnue. Les résidus s’emboîtaient étroitement sur une courbe
mathématique, d’un type avec lequel je n’étais pas immédiatement familier. J’ai
cherché de l’aide dans cette difficulté auprès de quelques amis mathématiciens
érudits, mais sans succès.
... Pour aider à la solution de la courbe des résidus, (Observations – Newcomb),
de l’obliquité de l’écliptique, j’ai examiné de nombreux types de courbes
mathématiques. Beaucoup d’entre eux ont des applications pratiques et ont une
interprétation précise, qui est donc mathématiquement certaine et sûre.
Enfin, dans l’ouvrage de Joseph Edwards, Differential Calculus, p. 102, la courbe que je cherchais se détachait sans équivoque, démontrant les principes à la fois de « l’insensibilité » et de l'« irrégularité ». Il s’agissait d’une « courbe sinusoïdale logarithmique ». (voir Fig. 3) Lorsque les échelles de temps et de degrés de déplacement de l’axe de la terre par rapport à la position normale ont été ajustées de manière à correspondre aux échelles de l’exemple, la courbe moyenne résultante des observations était une réplique exacte de la courbe sinusoïdale logarithmique particulière illustrée dans le manuel. La courbe d’observation moyenne correspondait exactement à cette courbe sinusoïdale logarithmique, comme « une main dans un gant ».
La date de verticalité de la courbe, 2345 av. J.-C.... coïncidait avec une « irrégularité », c’est-à-dire un changement important et soudain de l’inclinaison de l’axe de la terre ; et la date de « l’insensibilité » ou de l’équilibre dans l’échelle de temps horizontale de la courbe, était de 1850 après J.-C.
Il était absolument certain que chaque point de la courbe d’observation moyenne de la figure 3 est précisément un point d’une courbe sinusoïdale logarithmique. La courbe est donc une démonstration mathématique certaine et certaine qu’en l’an 2345 av. J.-C., l’axe de la terre a été soudainement déplacé par un impact majeur ; et la courbe illustrée à la figure 3 est une courbe de la récupération partielle de la terre à un état d’équilibre, à son inclinaison et à ses conditions normales, comme atteint en 1850 après J.-C.
Il convient de noter ici que les dates correspondant à la verticalité et à l’horizontalité complète de la courbe ne dépendent pas d’une sélection isolée ou arbitraire des observations, mais qu’elles sont déterminées par le contour complet de la courbe, qui se conforme à un modèle mathématique défini et précis tout au long de son parcours.
Un examen attentif de la relation entre les observations et la courbe moyenne a ensuite montré qu’elles étaient disposées en groupes alternativement au-dessus et au-dessous de la courbe moyenne, avec une période d’environ 600 ans entre les groupes. En résolvant ce problème par ce qu’on appelle la « méthode de l’analyse harmonique », j’ai constaté que c’était effectivement le cas, et j’ai pu établir une formule satisfaisant à ces conditions.
Cette formule, représentée sous forme graphique dans la figure 4, donne ce qu’on appelle une « courbe sinusoïdale harmonique à amplitude décroissante », l’amplitude, ou l’écart au-dessus ou au-dessous de la position moyenne, étant un maximum au début de la courbe, en 2345 av. J.-C., et se réduisant progressivement à zéro à sa fin, en 1850 après J.-C. C’est la caractéristique de la façon dont un corps en rotation libre, comme la terre dans sa rotation quotidienne, est rétabli à un état stable après une perturbation soudaine de son axe.
La présence de cette courbe sinusoïdale harmonique, avec son amplitude décroissante, est une merveilleuse confirmation du fait important, et maintenant vérifié, que la terre a progressivement fait une récupération partielle, au cours de l’intervalle de 4194 ans de 2345 av. J.-C., à 1850 ap. J.-C., après une grande perturbation soudaine de son axe en 2345 av. J.-C. et qu’il a atteint son état actuel d’équilibre achevé en 1850 après J.-C.
En 1935, j’ai envoyé un document préliminaire à la Royal Astronomical Society, traitant des résultats obtenus jusqu’à présent à l’époque. Il m’a été renvoyé par des arbitres, avec une note indiquant que les erreurs des anciennes observations nécessitaient une discussion plus approfondie. C’était l’opinion générale des astronomes de l’époque, et c’est encore le cas, que les différences entre les anciennes observations de l’obliquité de l’écliptique et la formule de Newcomb sont entièrement dues à des erreurs dans les anciennes observations. Cependant, il est maintenant démontré que cette opinion a besoin d’être révisée, à la lumière de l’examen de la question donnée au chapitre 2 de L’obliquité de l’écliptique.
Les conseils donnés à l’époque par les critiques étaient des plus précieux, et j’ai décidé d’examiner les conditions d’erreur dans les observations anciennes d’une manière pratique, en construisant et en utilisant un type de gnomon vertical pour les observations solstitielles du soleil, similaire aux gnomons utilisés dans les temps anciens. Cela a été minutieusement testé à l’Université d’Adélaïde au solstice de juin (hiver austral) de l’année 1936. Neuf observateurs ont pris part aux observations, et 172 observations ont été faites. Ils sont décrits au chapitre 2. Les résultats confirment l’exactitude générale des observations anciennes, à une ou deux minutes près de l’arc ; et ils montrent aussi que dans une longue série d’observations de ce genre faites par un observateur attentif (comme les observations faites par Eratosthène pendant ses 40 ans de travail à Alexandrie), il n’y a pas de grandes erreurs.
L’étape suivante consistait à écrire un compte rendu complet de toute l’affaire, ainsi qu’une étude de l’astronomie des temples solaires d’Égypte, en particulier du grand temple solaire d’Amen-Ra à Karnak, qui était orienté vers le soleil couchant au solstice d’été à la date de sa fondation, vers 2045 av. J.-C. Parallèlement à cela, il fallait étudier l’ancien monument calendaire britannique de Stonehenge, qui était orienté par ses constructeurs au point de lever du soleil au solstice d’été dans les temps anciens ; et, en outre, l’ancien grand temple solaire péruvien de Tiahuanaca, près du lac Titicaca, dans la Cordillère des Andes en Bolivie, conçu par ses constructeurs pour l’observation des points de lever du soleil aux solstices d’été et d’hiver.
Tous ces anciens temples ou monuments solaires jettent une lumière très intéressante sur l’obliquité de l’écliptique dans les temps anciens, et sont en plein accord avec les résultats obtenus à partir des anciennes observations astronomiques faites par les Chinois, les Hindous et les Grecs, telles que décrites dans les chapitres 3, 4 et 5.
J’espérais que
ce travail pourrait être publié en tant que produit de l’Observatoire
d’Adélaïde, pour être distribué à d’autres observatoires et pour que les
astronomes puissent l’examiner. Mais sa publication a été retardée.
George F. Dodwell
Wayville, Australie-Méridionale, octobre 1962.
* Décrit dans : [Drayson,
Alfred Wilks :] Un terrain inexploré en astronomie et en
géologie, donnant plus de détails sur la seconde
rotation de la terre et sur les calculs importants qui peuvent être faits à
l’aide d’une connaissance de celle-ci. Par le major-général A.W. Drayson
... Londres, K. Paul, Trench, Trübner and Co. Ltd., 1890. Retour
au texte
Dans ce
travail, qui a pris de nombreuses années, il est montré que les observations
antiques et médiévales de l’obliquité de l’écliptique (qui est une mesure de
l’inclinaison de l’axe de la Terre par rapport à la perpendiculaire à son
orbite), diffèrent de la courbe régulière, correspondant à la formule
internationalement acceptée de Newcomb, d’une quantité de plus en plus grande à
mesure que nous remontons dans l’antiquité.
De plus, ces différences atteignent un maximum unique en l’an 2345 av. J.-C.
Lorsque les différences, ou « résidus » comme on les appelle habituellement,
sont étudiées, on trouve qu’elles tracent une courbe logarithmique exacte,
c’est-à-dire une courbe de « sinus logarithmiques », qui a une oscillation
périodique secondaire, ou « courbe sinusoïdale harmonique », avec une amplitude
décroissante, superposée.
L’interprétation de cette courbe combinée est qu’il s’agit d’une récupération
après une perturbation de l’axe de la Terre, qui s’est produite en l’an 2345 av.
J.-C.
Une déclaration générale concernant le mouvement de l’axe de la Terre est donnée
au chapitre 1. À la fin de ce chapitre se trouve une liste des déterminations de
l’obliquité de l’écliptique, à partir de laquelle la courbe a été dérivée ; en
outre, des données tabulaires sont fournies pour la formule de Newcomb et pour
la nouvelle courbe d’obliquité ; aussi un tableau des réductions du bord de
l’ombre au centre du soleil, 1900 à 2000 av. J.-C., à utiliser dans le calcul
des observations de gnomons.
Le chapitre 2 rend compte des erreurs auxquelles les observations anciennes étaient sujettes, et des corrections appliquées pour obtenir la vraie valeur à chaque date d’observation.
Les chapitres 3
à 7 rendent compte des observations de l’obliquité de l’écliptique faites par
les anciens Chinois (3) ; Hindous anciens (4) ; Grecs anciens (5) ; les Arabes
et les Perses médiévaux (6) ; et enfin les observations européennes, médiévales
et modernes (7). Les chapitres 8 à 10 rendent compte de ces célèbres monuments
de l’Antiquité, orientés vers le soleil aux solstices, à Karnak et en d’autres
endroits d’Égypte, de Stonehenge en Angleterre et de Tiahuanaco au Pérou.
LE MOUVEMENT DE L’AXE DE ROTATION DE LA TERRE EST LA
PREUVE D’UNE
PERTURBATION DE L’AXE DE LA TERRE DANS L’ANTIQUITÉ
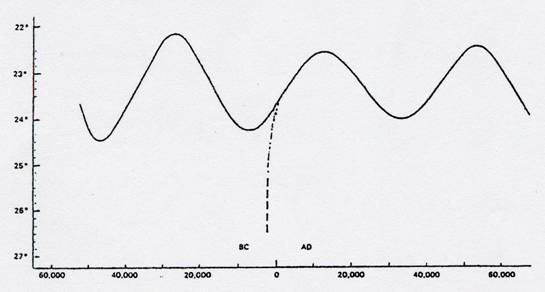
La figure 1, ci-dessous, est un graphique de la variation régulière et périodique de l’inclinaison de l’axe de rotation de la Terre, généralement connue sous le nom de variation séculaire, c’est-à-dire séculaire, de l’obliquité de l’écliptique. Elle est due à l’attraction gravitationnelle des planètes sur la Terre, interagissant avec l’attraction du Soleil et de la Lune sur la protubérance équatoriale de la Terre.
Dans ce graphique, la courbe normale de l’obliquité de l’écliptique est tracée pour trois oscillations. La courbe est dérivée de la formule complète donnée par l’astronome américain J.N. Stockwell (Smithsonian Contributions to Knowledge, Vol. 18. 1873, Article 3).
FIGURE 1
: OBLIQUITÉ DE L’ÉCLIPTIQUE SELON STOCKWELL.
Courbe montrant les valeurs maximales et minimales, et la période de la
variation, selon Stockwell
Courbe montrant les valeurs maximales et minimales, et la période de la
variation selon la formule de Stockwell

Cette formule, dit Stockwell, nous permet d’obtenir les valeurs numériques de l’obliquité pendant tous les âges passés et futurs. De la courbe, nous voyons que l’obliquité, qui est maintenant (en 1954) de 23º 26' 43", diminue progressivement jusqu’à un minimum de 22º 30' vers 13 000 après J.-C. ; et qu’elle était à son dernier maximum, 24º 12', environ 7000 av. J.-C.
Les résultats obtenus par Stockwell ont été légèrement modifiés par les recherches ultérieures de l’astronome américain Simon Newcomb, dont la formule, bien que plus précise pour les temps récents, n’est pas strictement applicable pendant plus de 2000 ou 3000 ans avant et après l’époque actuelle. La formule de Newcomb a été adoptée par les astronomes comme la formule internationale pour la variation séculaire, ou séculaire, de l’obliquité de l’écliptique, dans les limites de temps que nous venons de mentionner, c’est-à-dire peut-être jusqu’à 1000 ou 2000 av. J.-C., et celle qu’elle suivra dans des âges similaires à venir. Je l’ai donc utilisé ici pour toutes les comparaisons avec les observations anciennes, médiévales et modernes de l’obliquité.
C’est la croyance générale des astronomes que la formule de Newcomb représente vraiment et très étroitement l’obliquité, dans les limites de temps mentionnées ; et les divergences entre les observations anciennes et médiévales par rapport à cette formule ont été attribuées par conséquent à des erreurs de ces observations, dues, pense-t-on généralement, à l’emploi d’instruments et de méthodes d’observation simples ou grossiers.
La figure 1 montre, à petite échelle, comment les écarts apparaissent lorsqu’ils sont présentés sur un graphique, et l’échelle est agrandie dans la figure 2. Les observations qu’ils représentent appartiennent à des époques et à des lieux très éloignés, ces derniers comprenant la Chine ancienne, l’Inde, l’Égypte, la Grèce et diverses parties de l’Asie Mineure et de l’Europe.
Ils s’accordent si constamment, à travers tous les temps et tous les lieux, à tracer une courbe s’écartant de plus en plus de la formule de Newcomb, à mesure que nous remontons à l’antiquité, que nous devons les examiner attentivement, pour examiner leur fiabilité, et pour voir quelle lumière ils jettent sur l’état primitif de l’inclinaison de l’axe de la Terre.
DÉPLACEMENT DE L’AXE DE LA TERRE.
On verra que la courbe, sur laquelle tombent les observations réelles, est une combinaison de
(1) l’oscillation normale, due à l’action du Soleil, de la Lune et des planètes sur la Terre, et représentée par la formule de Newcomb ; et
(2) une courbe « sinusoïdale logarithmique », ayant également une courbe « sinusoïdale harmonique », avec une amplitude décroissante superposée à celle-ci. C’est ce que montrent les figures 3 et 4.
L’interprétation mathématique de ce second type de courbe est qu’il s’agit d’une courbe de récupération après une perturbation de l’axe de la Terre, l’état final d’équilibre n’ayant été atteint que récemment, c’est-à-dire vers le milieu du XIXe siècle, ou vers 1850 après J.-C. C’est pourquoi aucune trace n’en est aujourd’hui révélée dans les observations faites avec des instruments modernes de haute précision, dans les grands observatoires d’aujourd’hui.
FIGURE 2
COURBE DE L’OBLIQUITÉ DE L’ÉCLIPTIQUE(
A) d’après la formule internationale de Newcomb.
b) D’après les observations.
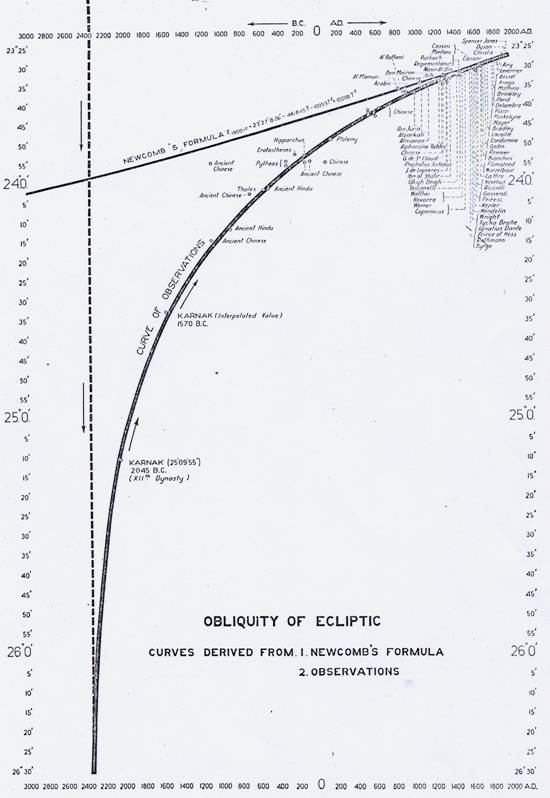
Voir le tableau de données pour la liste des observations
Cependant, le
mouvement était encore suffisamment évident, au XVIIe siècle, pour être
perceptible dans les observations faites par Flamsteed (le premier astronome
royal d’Angleterre, à l’observatoire de Greenwich), et dans les observations
aussi dans les observations d’autres astronomes célèbres de cette période. C’est
beaucoup plus visible dans les temps anciens. Néanmoins, si l’on considère
quelques-unes des observations anciennes les mieux connues, telles que celles
d’Eratosthène, 230 av. J.-C., et d’Hipparque, 135 av. J.-C., (lorsque la
différence était jusqu’à 8 ¢ plus grande que la valeur de Newcomb), la confiance
des astronomes dans la formule de Newcomb est si forte, qu’ils n’ont pu que
conclure que ces anciennes observations sont toutes erronées. dans la mesure
exacte où ils diffèrent de Newcomb.
Notons cependant que Tannery, l’éminente autorité française en matière
d’astronomie ancienne, avait une meilleure opinion de la valeur des observations
grecques antiques. Il montre que la fameuse et exacte première mesure de la
circonférence de la terre, qui fut faite par Ératosthène, en 230 av. J.-C.,
n’était « nullement le résultat d’un heureux accident », et dans L’Astronomie
Ancienne, p. 120, il fait les remarques suivantes concernant la mesure par
Ératosthène de l’obliquité de l’écliptique :
Avant la mesure d’Ératosthène, l’Obliquité était évaluée à 1/15 du cercle, soit 24 degrés. Cette détermination, indiquée par Eudème sur le rapport de Dercyllide (Théon de Smyrne), était déjà incontestablement connue d’Eudose, et peut-être était-elle antérieure à lui, remontant à l’école de Pythagore. Elle est évidemment liée à la solution donnée par Euclide du problème de l’inscription dans un cercle du pentagone régulier, cette solution ayant pour objet le traçage du cercle moyen du Zodiaque sur la sphère céleste. Le processus à suivre pour mesurer l’obliquité de l’écliptique était alors connu dès le début de l’astronomie grecque. Le rôle qu’a joué Ératosthène a été de douter de l’exactitude de la simple relation universellement admise devant lui, et d’entreprendre une mesure qu’il a su rendre si exacte qu’elle a fait désespérer ses successeurs de faire mieux.
Tannery souligne également qu’Eratosthène « s’en tint naturellement au procédé, déjà familier dans toutes les villes grecques, d’observer les ombres du gnomon ». (Voir, en outre, le compte rendu détaillé de ces observations fait, sur une période de plusieurs années, par Ératosthène)
En ce qui concerne la suggestion de Tannery selon laquelle la détermination de 24 degrés pour l’obliquité de l’écliptique remonte à l’école de Pythagore, nous pouvons maintenant voir que cette suggestion est correcte. Pythagore est né à Sidon en Syrie vers 580 av. J.-C., soit quelques années plus tôt. Il a été élevé à Samos, la résidence principale de son père. Il a commencé à voyager à la recherche de la connaissance à l’âge de 18 ans ; à Milet, il s’entretint avec Thalès. Il voyagea ensuite en Phénicie et en Syrie, puis en Égypte, où il passa 22 ans à étudier, qui se terminèrent par la conquête de l’Égypte par Cambyse en 525 av. J.-C. En Égypte, il étudia surtout la géométrie et l’astronomie, et étendit le théorème du « carré de l’hypoténuse » à tous les triangles rectangles, ce théorème étant depuis associé à son nom. Jamblice nous dit qu’il pratiqua l’astronomie dans les temples égyptiens pendant tout son séjour en Égypte.
Il fut emmené à Babylone en captivité, mais continua ses études parmi les Chaldéens et les Magoi perses. Après cela, il visita l’Inde, la Celtique, la péninsule ibérique et la Sicile, puis s’installa à Crotone dans le sud de l’Italie. Nous pouvons donc conclure que l’école de Pythagore, où il effectua des observations astronomiques, fut établie à Crotone vers l’an 515 av. J.-C.
D’après la nouvelle formule, l’obliquité de l’écliptique à cette période était de 24 degrés, 0 minute, 5 secondes. Par conséquent, Tannery a eu raison d’attribuer la valeur de 24 degrés à une date correspondant à l’école de Pythagore.
Considérons maintenant d’un peu plus près ce résultat d’obliquité de 24 degrés, associé au nom de Pythagore. Pythagore était un disciple de Thalès, le premier des Sept Sages de Grèce, qui lui-même a également fait des mesures de l’Obliquité de l’Écliptique, et a obtenu le même résultat, 24 degrés. On peut considérer comme certain que Thalès a utilisé le gnomon vertical pour ces mesures, car il était un parent, un compagnon et un concitoyen à Milet de son célèbre jeune philosophe grec contemporain, Anaximandre, qui, ayant appris l’utilisation du gnomon vertical des Chaldéens, est remarquable pour avoir été le premier à introduire son utilisation en Grèce. Avec lui, il (Anaximandre) a observé l’Obliquité de l’Écliptique. Il installa également le premier cadran solaire dans un endroit ouvert à Lacédémone.
Le gnomon vertical est devenu connu des Grecs sous le nom de scioterion (« preneur d’ombres »), ou héliotropion (« instrument pour observer le soleil aux solstices »). Il n’y a pas de doute que Pythagore utilisait cet instrument dans son école de Crotone, et qu’il observait avec lui l’altitude du soleil à midi aux solstices d’été et d’hiver. C’était plusieurs siècles avant l’introduction d’autres types d’instruments astronomiques également utilisés par les astronomes grecs d’une période ultérieure à Alexandrie. De ces observations, Pythagore aurait obtenu, (tout comme Eratosthène l’a fait près de trois siècles plus tard), le double angle d’obliquité, en soustrayant l’altitude observée du soleil à la mi-journée, au solstice d’hiver, de son altitude correspondante à mi-jour au solstice d’été. Ce double angle d’obliquité était de 48 degrés, dont la moitié, 24 degrés, est l’obliquité de l’écliptique associée par la tannerie au nom de Pythagore.
A ce propos, nous pouvons noter que les anciens astronomes grecs donnent parfois l’angle double (ou intertropical) double (ou intertropical) de l’obliquité, comme dans le cas de Thalès (48 degrés), d’Ératosthène (47 degrés, 42,5 minutes, d’où la demi-partie ou l’obliquité - 23 degrés 51 minutes 15 secondes - est dérivée), et Hipparque (le même qu’Ératosthène).
En accord avec cela, Ptolémée dans sa Syntaxe, affirme que le double angle de L’obliquité observée par Ératosthène et Hipparque était inférieure à 47 degrés 45 minutes, mais supérieure à 47 degrés 40 minutes (valeur moyenne 47 degrés 42,5 minutes), dont la moitié donne l’obliquité à 23 degrés, 51 minutes 15 secondes, comme nous l’avons déjà dit. Parfois, cependant, ils donnent le rapport de ce double angle à l’ensemble du cercle de 360 degrés. Ainsi, Hipparque donne le rapport de 11 à 83 pour l’angle intertropical total par rapport à l’ensemble du cercle ; cela équivaut à 47 degrés 42 minutes 39 secondes, d’où l’on obtient l’obliquité de 23 degrés 51 minutes 20 secondes, également attribuée à Hipparque.
Une autre méthode utilisée par les Grecs de l’Antiquité consistait à donner le rapport entre la hauteur du gnomon et la longueur de l’ombre à l’un ou l’autre des solstices ou aux deux. À titre d’exemple, Pythéas, l’explorateur de l’Antiquité grecque, lors de son voyage de découverte en 326 av. J.-C., érigea à Marseille, au solstice d’été, un grand gnomon, divisé en 120 parties, et donna le rapport de la hauteur du gnomon à la longueur de l’ombre comme 120 à 41 4/5 (selon Strabon), ou (selon Ptolémée) comme 60 à 20 5/6 ou 120 à 41 3/5. L’utilisation de ces grands rapports, alors qu’un rapport plus simple n’était pas possible, indiquait que les astronomes grecs de l’Antiquité prenaient un soin considérable à leurs observations et ne donnaient pas simplement des « nombres ronds ».
|
* Ces « parties » étaient peut-être des dixièmes de l’ancien standard grec « pied olympique », dont la longueur était de près de 1,013 pied anglais. La division décimale du pied était en usage dans l’Égypte et la Chine anciennes, et a sans doute été adoptée aussi par les Grecs. Dans ce cas, le « grand gnomon » utilisé par Pythéas aurait eu une hauteur de 12 pieds olympiques, ce qui équivaut à 12 pieds 1 1/2 pouces de mesure anglaise ; et la longueur de l’ombre de midi au solstice d’été, 41 4/5 parties, telle que donnée par Strabon, aurait été de 4 pieds 2 4/5 pouces en mesure anglaise. |
Dans le cas des observations que l’on croit avoir été faites par Pythagore à Crotone dans le sud de l’Italie (latitude 39 degrés 7 minutes nord), vers 515 av. J.-C., un simple calcul montre une différence flagrante dans les longueurs d’ombre d’un gnomon de 8 pieds au solstice d’hiver, selon que nous supposons que l’obliquité est de 23 degrés 45 minutes 30 secondes. donné par la formule de Newcomb pour cette année-là, soit 24 degrés entiers, attribués à Pythagore.
Car, dans le premier cas, la longueur de l’ombre d’hiver aurait été de 15 pieds 5,4 pouces (Newcomb), alors qu’elle aurait été de 15 pieds 7,3 pouces, c’est-à-dire une différence de 1,9 pouce. Nous ne pouvons pas penser que Pythagore aurait pu ignorer une si grande différence. Un critère similaire s’applique également aux observations formulées par Thales. Quelle qu’ait pu être la hauteur des gnomons qu’ils ont utilisés, nous pouvons à juste titre avoir confiance dans l’exactitude substantielle de leurs observations.
Les observations de Thalès et de Pythagore sont également confirmées par les résultats hindous, tirés de l’astronomie du Surya Siddhanta, à peu près à la même époque ; et le fait est que la formule de Newcomb diffère de toutes les observations faites à cette époque par la quantité étonnamment grande de 15 minutes d’arc, ou 1/4 de degré. Puisque la formule de Newcomb représente vraiment les facteurs gouvernant le changement de l’obliquité tel que nous le connaissons, nous ne pouvons que conclure soit que les anciennes observations sont grandement erronées, soit qu’il peut y avoir eu un autre facteur causant un changement, et qui n’a pas été mis en lumière jusqu’à présent.
Afin d’examiner l’exactitude de cette explication, j’ai commencé le récit des observations anciennes par l’étude des erreurs auxquelles étaient sujettes, en particulier, les observations faites avec le gnomon vertical, ou pôle d’ombre, puisque c’était l’instrument le plus fréquemment utilisé dans les temps anciens pour les observations de l’altitude du soleil aux solstices. Il a d’ailleurs été régulièrement utilisé pour de telles observations en Chine pendant une période de plus de 2000 ans, dès 1100 av. J.-C. Les Chinois considéraient qu’il était si important d’établir l’uniformité des observations, qu’ils fixèrent par la loi la hauteur du gnomon à 8 pieds.
Le gnomon était également utilisé par les anciens hindous et par les Grecs. À une date ultérieure, à partir de l’époque d’Ératosthène, en 230 av. J.-C., les astronomes grecs introduisirent des armilles et d’autres instruments circulaires ; mais le gnomon restait toujours d’usage général, et Ptolémée et Strabon enregistrent régulièrement les latitudes en termes de hauteur du gnomon à la longueur de son ombre.
Lors du renouveau de l’astronomie au IXe siècle après J.-C., les Arabes et d’autres astronomes médiévaux ont également utilisé le gnomon pour observer l’altitude du soleil, et c’était l’instrument méridien standard des grands observatoires de Paris et de Saint-Pétersbourg jusqu’au milieu du XVIIIe siècle.
Les résultats obtenus avec le gnomon sont si bien dans les limites d’erreur requises pour la présente recherche, que les observations faites avec lui dans les temps anciens méritent une attention particulière. Ils montrent que les grandes divergences par rapport à la formule de Newcomb ne sont pas simplement dues à des erreurs d’observation, mais indiquent un autre facteur, qui appelle une explication. Si l’on tient compte de toutes les sources d’erreur, les observations médiévales et anciennes de l’obliquité se trouvent constamment sur une courbe, illustrée à la figure 2, qui est en accord avec la formule de Newcomb à l’époque moderne, mais qui diffère grandement de celle-ci il y a 2000 ou 3000 ans.
Si la courbe des anciennes observations se poursuit en arrière, elle devient
plus raide ; et vers l’an 2045 av. J.-C., il donne une valeur de l’obliquité
supérieure à 25 degrés. C’est plus de 1 degré de plus que la valeur de Newcomb,
qui est de 23 degrés, 55 minutes 55 secondes pour cette date. Enfin, en l’an
2345 av. J.-C., la courbe devient exactement verticale et indique une valeur
probable et réelle d’environ 26 1/2 degrés pour cette date.
Une confirmation remarquable de l’obliquité en l’an 2045 av. J.-C. est donnée par le temple solaire orienté d’Amen Ra à Karnak, en Égypte, le plus grand temple qui ait jamais été construit. Ceci est décrit au chapitre 8. Des inscriptions hiéroglyphiques, gravées dans le granit, montrent que les anciens Égyptiens prenaient grand soin d’orienter leurs temples solaires. Les rayons du soleil levant ou couchant, à certaines dates importantes, brillaient alors directement le long de la longue allée centrale, ou axe du temple, dans le sanctuaire sombre et illuminaient l’image du dieu-soleil qui s’y trouvait.
Dans le grand temple solaire de Karnak, cela s’est produit au coucher du soleil le jour du solstice d’été. Il sera montré qu’en 2045 av. J.-C., date de fondation du Temple, la déclinaison solstitielle du soleil, ou distance maximale de l’équateur céleste, était de 25 degrés, 9 minutes et 55 secondes. Cette valeur est en accord exact avec le prolongement de la courbe des observations anciennes, et dépasse la valeur de Newcomb pour cette date de 1 degré 14 minutes. Une confirmation supplémentaire, à d’autres points de la courbe, est donnée par les célèbres monuments solaires de Stonehenge, en Angleterre, et de Tiahuanaco, au Pérou.
COMPARAISON DE LA FORMULE DE NEWCOMB AVEC LES OBSERVATIONS ANCIENNES
Nous devons
maintenant considérer la relation entre les deux courbes. C’est ce que montrent
graphiquement les figures 1 et 2.
a) La formule de Newcomb
La formule de Newcomb pour l’obliquité de l’écliptique, telle qu’adoptée par le
Congrès astronomique international de 1896, et utilisée depuis lors par un accord international, est la suivante :
E (1900 + T) = 23º.27'08.26 – 46 ».845T – 0 ».0059 T2 + 0 ».00181T3
où E = l’obliquité de l’écliptique
T = le nombre de siècles à partir de 1900 apr. J.-C., pris comme « + » pour les siècles après 1900 apr. J.-C., et « ... » pour les siècles avant 1900 apr. J.-C.
b) L’étendue de l’obliquité
L’étendue totale de la variation de l’obliquité de l’écliptique a été calculée par Laplace, en 1825, pour être limitée à 3º 7' 30 », ou 1º 33' 45 » de chaque côté de la valeur moyenne. (1)
Plus tard, en 1872, l’astronome américain J.N. Stockwell, en utilisant des déterminations plus précises des masses des planètes, a montré que « Les limites de l’obliquité de l’écliptique apparent à l’équateur sont de 24º 35' 38 » et 21º 58' 36 », d’où il s’ensuit que les plus grandes et les plus petites déclinaisons du soleil ne peuvent jamais différer les unes des autres dans une plus grande mesure que 2º 37' 22 » ..... Les périodes de changements séculaires ..... varient entre 26 000 et 53 000 ans. (2)
La figure 2 montre la relation entre la courbe des observations et celle de la formule de Newcomb jusqu’à 3000 av. J.-C., à une échelle plus grande que dans la figure 1, et avec plus de détails.
LA NOUVELLE COURBE DE L’OBLIQUITÉ POUR LES ÂGES PASSÉS
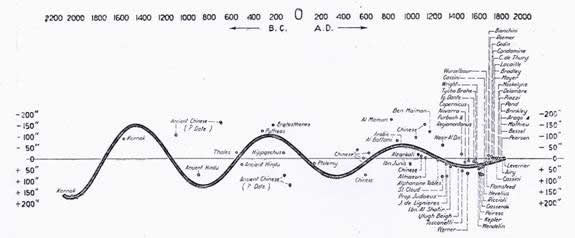
Pour savoir ce que c’est, la position solstitielle ou la déclinaison du soleil, au nord ou au sud de l’équateur céleste, est considérée comme la position normale pour une date donnée, et est soustraite de la déclinaison observée à cette date. Nous obtenons ensuite un ensemble de différences, ou « résidus », qui se trouvent sur ou près de la courbe lisse illustrée à la figure 3.
FIGURE 3
Courbe des résidus (courbe dérivée), montrant la
courbe sinusoïdale logarithmique par rapport aux observations

Sur la figure 3, la ligne horizontale supérieure montre l’échelle des dates de 3000 av. J.-C. à 2000 apr. J.-C. À l’extrême gauche, dans la colonne verticale, les degrés et les minutes de l’échelle verticale sont indiqués, en lisant verticalement vers le bas de 0º à 2º 35'. Les résidus (c’est-à-dire les différences entre la formule de Newcomb et les valeurs observées) sont tracés en référence à ces deux échelles, et la courbe moyenne qui les relie est tracée, comme le montre la figure.
On verra par l’inspection que lorsque la courbe est produite vers le bas, elle tend à devenir verticale vers la date de 2345 av. J.-C. En continuant la courbe vers le haut, elle devient complètement horizontale vers la date de 1850 après J.-C. Cette courbe est logarithmique. Elle correspond exactement à une courbe de « sinus logarithmiques ». Le lecteur qui connaît bien les courbes mathématiques peut le reconnaître immédiatement par inspection.
Il peut également être représenté de manière graphique (voir Fig. 3). Pour ce faire, nous écrivons sous l’échelle des dates des siècles avant J.-C. et après J.-C., sur la ligne horizontale supérieure, une échelle de degrés de 0° à 90°. Le début de cette échelle de degrés, 0, est à 2345 av. J.-C., où la courbe est verticale ; et la fin de l’échelle de degrés, 90º, est à 1850 après J.-C., où la courbe est complètement horizontale. La période complète couverte par la courbe est donc de 4194 ans, et chaque degré de l’échelle correspond à 46,6 ans.
Nous construisons maintenant une colonne verticale (colonne 2) des valeurs numériques des sinus logarithmiques, de 90º à 0º, tirées d’un livre de logarithmes. Le point de départ de cette colonne, sur le côté gauche de la « ligne zéro », est le sinus logarithmique de 90 degrés, à savoir 10,0000. Il s’agit d’un point final sur la courbe de 1850 après J.-C., où la courbe se termine horizontalement.
Les nombres indiqués dans la colonne 2 et les degrés et minutes dont ils sont les sinus logarithmiques sont indiqués dans le tableau suivant.
TABLEAU I
|
Colonne 2 de la
Fig. 3 : sinus logarithmiques
|
Degrés et minutes dont les nombres
de la colonne 2 sont les sinus logarithmiques |
|
10.0000
|
90º 00'
|
|
9.9000
|
52º 36'
|
|
9.8000
|
39º 07'
|
|
9.7000
|
30º 04'
|
|
9.6000
|
23º 28'
|
|
9.5000
|
18º 26'
|
|
9.4000
|
14º 33'
|
|
9.3000
|
11º 31'
|
|
9.2000
|
9º 07'
|
|
9.1000
|
7º 14'
|
|
9.0000
|
5º 44'
|
|
8.9000
|
4º 27'
|
|
8.8000
|
3º 37'
|
|
8.7000
|
2º 52'
|
|
8.6000
|
2º 17'
|
|
8.5000
|
1º 49'
|
|
8.4000
|
1º 26'
|
|
8.3000
|
1º 09'
|
|
8.2000
|
0º 54'
|
|
8.1000
|
0º 43'
|
|
8.0000
|
0º 34'
|
|
7.9333
|
0º 29'
|
On peut voir qu’il existe une relation d’échelle simple entre les nombres de la colonne 2 et ceux de la colonne 1 de la figure 3 (c’est-à-dire les résidus ou les différences entre les obliquités de Newcomb et les obliquités observées), à savoir qu’une différence de 0,1000 dans les nombres de la colonne 2 équivaut à une différence de 7,5' dans la colonne 1. Cela permet de placer les chiffres de la colonne 2 à leur position exacte sur le graphique.
La relation des coordonnées horizontales et verticales est alors telle que, si des paires de droites, horizontales et verticales, sont tracées sur le graphique à partir des points indiqués par le tableau ci-dessus, chaque paire se rencontrera exactement sur la courbe d’observation.
Ainsi, ils sont tous tout à fait d’accord pour montrer que la courbe qui correspond aux observations anciennes, médiévales et récentes entre 2345 av. J.-C. et 1850 apr. J.-C., n’est autre qu’une courbe sinusoïdale logarithmique exacte.
Ce type de
courbe est illustré dans Differential Calculus 1896
de J. Edwards, p. 102. Il s’agit d’une courbe de récupération, avec
rétablissement de l’équilibre après une perturbation ; et il montre avec
certitude qu’une perturbation de l’axe de la terre s’est produite à la date de
2345 av. J.-C., correspondant à l’extrémité 0º de la courbe ; et que son retour
à l’équilibre a été achevé en l’an 1850, ce qui correspond à l’extrémité 90º de
la courbe.
La coïncidence exacte de la courbe moyenne des observations avec une courbe
sinusoïdale logarithmique, combinée à la relation d’échelle simple que nous
venons de souligner, nous permet d’obtenir une formule numérique pour cette
courbe des résidus.
La formule est la suivante :
d1 ε = 75' x (10,0000000 – log sin (T1 x 2,14592 º) (voir note)
où d1 ε = la différence entre la formule de Newcomb et n’importe quel point de
la courbe moyenne des observations, et
T1 = le nombre de siècles après 2345 av. J.-C.
Cette formule nous permet de calculer la valeur de la courbe moyenne pour n’importe quelle date entre 2345 av. J.-C. et 1850 apr. J.-C.
|
note : Ce
nombre est obtenu en divisant 90º par 41,94, le nombre de siècles
dans l’intervalle entre 2345 av. J.-C. et 1850 ap. J.-C. Alors le
nombre de degrés par siècle est de 90º/41,94 = 2,14592 º |
Dans une courbe sinusoïdale logarithmique, la valeur numérique à 0º est infinie. Par conséquent, juste au début, cette courbe ne parvient pas à représenter le phénomène tel qu’il se produit réellement, puisqu’il a un commencement fini. Néanmoins, peu de temps après cette irrégularité initiale, la courbe représentant le phénomène se rattache normalement à la courbe sinusoïdale logarithmique, et continue ainsi jusqu’à la fin.
D’après l’étude du point de départ d’autres phénomènes naturels, qui s’accordent avec une courbe sinusoïdale logarithmique (par exemple, la première ou la phase majeure de la courbe de lumière d’une nouvelle étoile après son explosion initiale), il semble probable que l’axe de rotation de la Terre ait été soudainement modifié par la force de l’impact en 2345 av. J.-C. d’une inclinaison initiale d’environ 5 degrés, par une quantité d’environ 21,5 degrés à une nouvelle inclinaison d’environ 26,5 degrés.
Il n’est pas facile d’imaginer les vastes mouvements et changements qui ont eu lieu au moment de l’impact, et qui ont été suivis de séquelles continues au cours des siècles suivants, en raison de l’ampleur des forces à l’œuvre, impliquant à la fois l’état externe et l’état interne de la terre. Nous pouvons noter, cependant, les traditions hébraïques à propos de certaines d’entre elles, et les déclarations de Halley et de Laplace.
Une autre circonstance unique, confirmant l’exactitude des conclusions précédentes, est observée dans l’analyse des différences entre les résultats individuels de la courbe sinusoïdale logarithmique moyenne illustrée à la figure 3. Conformément à la loi des erreurs, ils sont répartis assez uniformément au-dessus et au-dessous de la courbe moyenne.
Mais à y regarder de plus près, ils semblent se regrouper en groupes, parfois légèrement au-dessus, parfois légèrement en dessous de la courbe moyenne ; L’intervalle de temps entre les groupes, de la valeur la plus élevée à la valeur la plus basse, est d’environ 600 ans.
Ils peuvent donc être examinés par la méthode de l’analyse harmonique. Dans un premier temps, ils sont tracés sur un graphique (figure 4) et on verra tout de suite qu’ils tombent sur une courbe subsidiaire d’oscillations. Il est important de noter qu’ils sont d’amplitude décroissante, étant beaucoup plus importants au début qu’à la fin, en 1850 après J.-C., où ils deviennent nuls.
Sept demi-oscillations sont indiquées entre 2345 av. J.-C. et 1850 apr. J.-C., la période exacte de demi-oscillation étant de 599 ans. Les points nodaux sont en 2345, 1746, 1147, 548 av. J.-C. et 52, 651, 1250, 1849-1850 ap. J.-C.
Les maxima et les minima sont alternativement aux dates intermédiaires, 2045, 1446, 847, 248 av. J.-C.; 352, 951 et 1550 ap. J.-C. De plus, lorsque des lignes limites sont tracées à travers les maxima et à travers les minima, elles convergent vers le point zéro à 1850 après J.-C., où la courbe principale ou moyenne est également terminée.
Cette date se
situe à l’époque des observations astronomiques exactes modernes ; de sorte
qu’il ne reste plus rien de la courbe moyenne ni des oscillations pour affecter
les observations modernes. Par conséquent, ce mouvement n’a pas attiré
l’attention des observateurs astronomiques au cours des 100 dernières années.
Un total de 59 observations [figures 3 et 4] (3),
soumises à une analyse harmonique des moindres carrés, donne la formule
suivante, exprimant une courbe sinusoïdale harmonique. Il permet de calculer
n’importe quel point de la courbe, en fonction de la date d’observation.
La formule est la suivante :
d2ε = (184 » – 3,82"T1) sin 30,043 º T1
Où d2ε est la différence par rapport à la courbe sinusoïdale logarithmique moyenne, et est alternativement positif et négatif ; et (T1) est le nombre de siècles à partir de 2345 av. J.-C.
Ces oscillations, sous forme agrandie, sont illustrées à la figure 4. Ils mettent en évidence une interaction des forces précessionnelles antérieures, affectant l’axe de la terre dans son ancienne position presque verticale [voir la note de Barry Setterfield], avec celles prédominantes ultérieures associées à sa nouvelle et plus grande inclinaison. La courbe des oscillations peut donc être considérée comme la résultante de ces forces, les dernières tendant à retarder, et les premières à hâter la précession. La courbe, qui est une courbe sinusoïdale harmonique, avec des amplitudes décroissantes, est en harmonie avec les conséquences de la perturbation d’un corps en rotation. Les oscillations sont expliquées par l’inertie du corps en rotation, qui ralentit et accélère alternativement la précession (4). La règle est énoncée comme suit :
i. Hâtez la précession, le sommet se lève. (5)
ii. Retardez la précession, le sommet tombe.
Il est évident que l’immense masse de la terre et sa viscosité interne jouent un rôle important dans la détermination de l’ampleur et de la période de ces oscillations.
En raison de sa rotation, la terre peut être considérée comme un gyrostat sur une très grande échelle ; et ce qui se passe en cas de perturbation est illustré par la voiture monorail Brennan, qui est équilibrée par un gyrostat. Lorsque la perturbation (dans le cas de la voiture monorail Brennan, une pression soudaine du vent) est appliquée, la voiture s’incline face au vent (la direction de l’inclinaison étant inversée par un dispositif spécial). La position finale inclinée est atteinte avec un certain élan, qui porte la voiture au-delà de la position neutre. La voiture dépasse la marque et revient, avec des oscillations d’amplitude décroissante, jusqu’à ce que le point stable soit atteint. (6)
L’analogie avec le retour de la Terre à un point stable en 1850 après J.-C., au cours de la période de 4194 ans après sa perturbation axiale en 2345 av. J.-C., est évidente. Les oscillations, ainsi révélées par l’analyse harmonique des observations, sont une confirmation frappante de la perturbation elle-même et du cours de la récupération de la terre dans les âges ultérieurs.
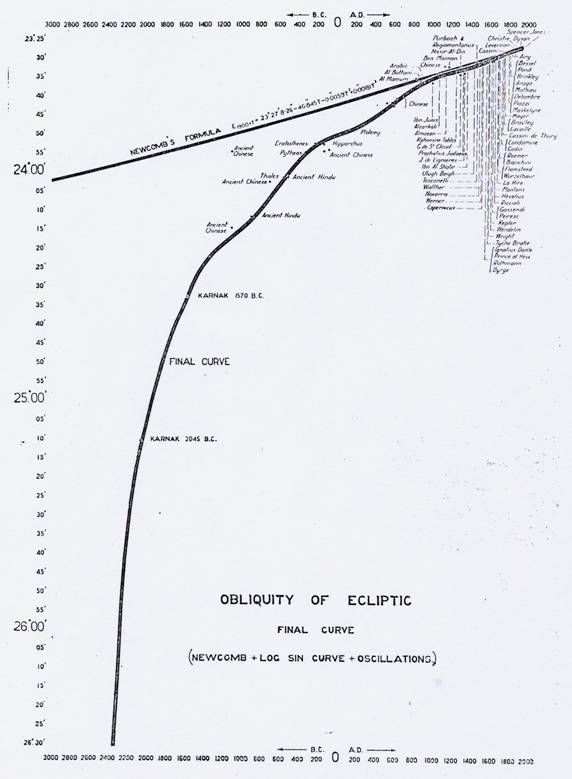
COURBE FINALE D'OBLIQUITÉ. GRAPHIQUE 5
Si nous combinons maintenant Formule de Newcomb avec la courbe sinusoïdale logarithmique moyenne, et avec la Courbe d’oscillations, nous obtenons la courbe finale d’obliquité, qui combine ces différents mouvements, entre les années 2345 av. J.-C., et 1850 apr. J.-C., (Figure 5). On verra d’un coup d’œil à quel point la les observations, en général, sont d’accord avec cette courbe finale.
(Cette courbe finale et les formules qui l’expriment, seront trouvées utiles dans les questions de Chronologie qui dépend des données astronomiques.)
En examinant la signification de la courbe sinusoïdale logarithmique, la question se pose de savoir si c’est la seule courbe qui pourrait être tracée pour s’adapter aux observations. Il a été suggéré qu’ils pourraient peut-être s’accorder avec une forme de courbe sinusoïdale, indiquant un mouvement périodique inconnu de l’axe de rotation de la terre. Les mouvements périodiques de l’axe de la terre, cependant, sont parfaitement connus ; et il n’y a aucune force disponible pour provoquer un mouvement supplémentaire.
Les principaux mouvements de l’axe de rotation de la terre, par ordre de découverte, sont les suivants :
(i) la précession
luni-solaire(ii) la nutation
(iii) la précession planétaire
Ce que l’on appelle la « précession générale » combine les précessions luni-solaire et planétaire. La précession luni-solaire est un mouvement giratoire (comme l’oscillation d’une toupie) de l’axe de la terre autour d’un point central, le pôle de l’écliptique, dans une période moyenne de 25 700 ans, cette période étant allongée à 25 800 ans par l’effet de la précession planétaire.
Le mouvement de précession de la terre a été l’une des grandes découvertes d’Hipparque, vers 124 av. J.-C.
Une modification de l’obliquité de l’écliptique, dépendante de la précession planétaire, a été suspectée pour la première fois par Ératosthène en 230 av. J.-C. Comme nous l’avons vu ci-dessus, Eratosthène trouva, d’après une longue série d’observations, que l’obliquité était de 23º 52' de son temps, de sorte qu’elle était de 8' de moins que la valeur de 24º transmise du temps de Thalès, en 558 av. J.-C., et de Pythagore, en 515 av. J.-C. ; soit une diminution de 8' en environ 300 ans.
Près de deux siècles et demi plus tard, vers l’an 14 apr. J.-C., à la fin du règne de l’empereur Auguste, le mathématicien romain Manilius nota un changement dans l’obliquité de l’écliptique, qu’il attribua soit à la course discordante du soleil lui-même, et à quelque changement dans le ciel, soit à un changement dans la terre universelle, par lequel il s’est éloigné de son centre, comme je l’ai détecté moi-même, et j’en entends parler aussi en d’autres endroits.
Cette conclusion remarquable a été tirée par Manilius à partir de ses observations, pendant 30 ans, des ombres solaires aux solstices d’été et d’hiver, projetées par le grand obélisque de Rome. Ce grand obélisque, de 75 pieds de haut, a été doté par Manilius d’une boule d’or à son sommet, et la position de l’ombre circulaire sur le trottoir plat en dessous a été soigneusement mesurée par lui, sur une période de 30 ans, avec une échelle de laiton fixée dans le pavement. (7)
Ce mouvement de la terre, ainsi qu’un supposé mouvement d’avant en arrière des points équinoxiaux, en vint à être associé plus tard aux théories de la « trépidation », qui était définie comme « un mouvement attribué au firmament, pour rendre compte de certains petits changements dans la position de l’écliptique et des étoiles ».
Copernic, en 1525, et Wendelin, le célèbre astronome belge, près de 100 ans plus tard, ont tenté d’expliquer la précession des équinoxes et la variation de l’obliquité de l’écliptique par des théories trépidationnelles. Cependant, ceux-ci n’étaient pas fondés sur des bases solides, et aucun principe physique n’a pu être trouvé pour expliquer les mouvements. La précession des équinoxes a été, en fait, inexplicable par les astronomes pendant 1800 ans, de l’époque d’Hipparque jusqu’à la grande découverte de l’attraction universelle par Sir Isaac Newton.
Dans les Principia de Newton, livre 3, Proposition 39, le problème du mouvement de précession de la terre a été, pour la première fois, correctement expliqué et calculé. Il a été démontré qu’elle était due à l’attraction gravitationnelle du soleil et de la lune sur la protubérance équatoriale de la terre.
Deux cents ans après Newton, Sir George Airy, le septième astronome royal d’Angleterre, a déclaré que « si nous pouvions présumer de choisir la partie des Principia qui a probablement étonné, ravi et satisfait ses lecteurs plus que toute autre, nous devrions nous fixer sans hésitation sur l’explication de la précession des équinoxes ».
Les Principia de Newton ont été publiés en 1697 ; et 60 ans plus tard, Bradley, le troisième astronome royal d’Angleterre, a achevé sa célèbre série d’observations des étoiles zénithales, qui a duré un cycle lunaire complet de 19 ans. Cela a abouti à sa découverte de la « nutation », un léger changement périodique dans le taux de précession, accompagné d’un changement annuel de 9,5 » dans l’inclinaison de l’axe de la terre, de chaque côté de sa position moyenne. La période complète était donc de 19 ans.
La découverte de Bradley a été publiée en 1748, et en l’expliquant, il a indiqué la véritable cause, que la « nutation » ou hochement de tête de l’axe de la terre, était due à la variabilité de l’action de la lune sur la protubérance équatoriale de la terre, en raison du déplacement de la lune sur une orbite inclinée de 5º 9' par rapport au plan de l’écliptique.
L’année suivante, l’éminent mathématicien français D’Alembert publia un traité dans lequel une analyse mathématique rigoureuse prouva de manière concluante que c’était exact, et, en outre, il confirma complètement l’explication de Newton sur la précession.
À l’époque de Newton, la diminution progressive de l’obliquité de l’écliptique n’avait pas été complètement établie. Certains astronomes, comme Tycho Brahe, Riccioli, Gassendi et Flamsteed, pensaient que les divergences, de l’Antiquité jusqu’à la leur, étaient dues à des erreurs d’observation.
Halley, le deuxième astronome royal d’Angleterre, était également de cet avis. L’année de la publication des Principia de Newton, en 1697, Halley présenta un article à la Royal Society, comparant les altitudes solstitielles du soleil observées à Nuremberg par Wurtzelbaur en 1686 avec des observations similaires faites dans la même ville par Bernard Walther 200 ans plus tôt. Dans cet article, il disait : « D’après ces observations, il semble que l’obliquité de l’écliptique est restée inchangée pendant ces 200 dernières années, c’est-à-dire que l’angle que fait l’axe de la terre avec le plan de l’écliptique, ou orbite dans laquelle elle se déplace chaque année autour du soleil, a été sans changement sensible pendant tout ce temps. »
Newton, cependant, avait montré dans les Principia, en termes généraux, que l’effet perturbateur des planètes produirait, entre autres choses, une altération de l’inclinaison du plan dans lequel une planète se meut. Il n’a pas fait de calculs sur l’importance de ce changement, mais il y a indiqué la cause qui, dans le cas de la terre, produit la variation séculaire de l’obliquité de l’écliptique.
La question des perturbations planétaires commença ainsi à attirer l’attention des astronomes, et en 1756 le mathématicien suisse Euler, dans une série d’articles, montra que l’effet de ces perturbations sur la terre ne serait pas seulement de provoquer un léger mouvement de la précession dans la direction opposée à celle produite par le soleil et la lune, mais aussi de faire diminuer l’obliquité de l’écliptique d’environ 48" en 100 ans ; Pas beaucoup plus de 1" de plus que la valeur réelle.
Près de 30 ans plus tard, le grand mathématicien Lagrange a montré que l’obliquité ne pouvait pas diminuer indéfiniment, mais que l’action des planètes ne pouvait provoquer que de petites oscillations dans les positions des différentes orbites, de sorte que, dans le cas de la terre, l’obliquité de l’écliptique était confinée dans de petites limites.
Laplace, en 1827, calcula que la portée totale de cette oscillation de l’orbite terrestre était de 3º 7' 30" ; mais un calcul ultérieur de Stockwell en 1873, utilisant des déterminations plus précises des masses des planètes, a rendu la portée totale un peu plus petite, à savoir 2º 37' 22" ; les limites de l’obliquité allant d’un minimum de 21º 58' 36 » à un maximum de 24º 35' 38 ».
Laplace, dans Le Système du Monde, Vol. 2. p. 211, a expliqué la variation en ces termes :
Si l’on se réfère à un plan fixe, à la position de l’orbite de la terre, et au mouvement de son axe de rotation, il apparaîtra que l’action du soleil, à la suite des variations de l’écliptique, produira dans cet axe un mouvement oscillatoire semblable à la nutation, mais avec cette différence, que la période de ces vibrations étant incomparablement plus longue que celle des variations du plan de l’orbite lunaire, l’étendue de l’oscillation correspondante dans l’axe de la terre est beaucoup plus grande que dans la nutation.
L’action de la lune produit dans ce même axe une oscillation semblable, parce que l’inclinaison moyenne de son orbite par rapport à celle de la terre est constante.
« Le déplacement de l’écliptique, en se combinant avec l’action du soleil et de la lune sur la terre, produit sur son obliquité à l’équateur une variation très différente de celle qui résulterait de ce seul changement de position ; l’étendue totale de cette variation serait, par cette altération de l’écliptique, d’environ 12 degrés, et l’action du soleil et de la lune la réduit à environ 3 degrés.
Stockwell a également commenté de la même manière l’interaction du soleil, de la lune et des planètes, dans la production de la variation de l’obliquité, comme suit :
Nous pouvons en mentionner ici quelques-unes parmi les nombreuses conséquences heureuses qui résultent de la forme sphéroïdale de la terre.
« Si la terre était une sphère parfaite, il n’y aurait pas de précession ou de changement d’obliquité résultant de l’attraction du soleil et de la lune ; Le cercle équinoxial formerait un plan invariable dans le ciel, autour duquel l’orbite solaire tournerait avec une inclinaison variant jusqu’à douze degrés, et un mouvement égal à la précession planétaire des points équinoxiaux.
"Le soleil, lorsqu’il est aux solstices, atteindrait, à certaines périodes de temps, la déclinaison de 29º 17' pendant plusieurs milliers d’années ; et encore, à d’autres périodes, seulement jusqu’à 17º 17'.
Les saisons seraient sujettes à des vicissitudes en fonction de la distance des tropiques à l’équateur, et la distribution de la lumière solaire et de la chaleur à la surface de la terre serait modifiée de telle sorte qu’elle changerait essentiellement le caractère de sa végétation et la distribution de sa vie animale.
Mais la forme sphéroïdale de la terre modifie tellement les changements séculaires dans les positions relatives de l’équateur et de l’écliptique, que les inégalités de précession et d’obliquité sont réduites à moins d’un quart de ce qu’elles seraient autrement.
Les périodes des changements séculaires, qui, dans le cas d’une terre sphérique, auraient besoin de près de deux millions d’années pour passer par un cycle complet de valeur, sont maintenant réduites à des périodes qui varient entre 26 000 et 53 000 ans.
Les mouvements séculaires, qui auraient lieu dans le cas d’une terre sphérique, sont tellement modifiés par l’état actuel du globe terrestre, que des changements dans la position de l’équinoxe et de l’équateur se produisent maintenant en quelques siècles, ce qui nécessiterait autrement une période de plusieurs milliers d’années.
« Cette considération est d’une grande importance dans les recherches sur l’antiquité et la chronologie réputées de ces anciennes nations qui ont atteint la compétence dans la science de l’astronomie, et dont les archives des travaux astronomiques sont le seul monument restant d’un peuple hautement intellectuel, dont toute autre trace de l’existence a disparu depuis longtemps. »
D’autres mathématiciens éminents, à partir de l’époque d’Euler, ont également contribué à la théorie des perturbations planétaires et du mouvement précessionnel ; de sorte qu’avant la fin du XIXe siècle, l’action du soleil, de la lune et des planètes sur l’axe de rotation de la Terre fut pleinement comprise et calculée avec précision.
En résumé, les forces extérieures qui agissent sur la terre et affectent son axe de rotation sont les attractions gravitationnelles du soleil, de la lune et des planètes. Parmi ceux-ci, le soleil et la lune sont à l’origine de la précession luni-solaire, consistant en un mouvement giratoire très lent de l’axe de la terre autour du pôle de l’écliptique comme centre, sur une période moyenne de 25 700 ans, allongée par la précession planétaire à 25 800 ans.
L’inclinaison de l’axe, cependant, est maintenue à un angle presque constant en ce qui concerne les changements d’une période relativement courte ; La principale variation de ce genre, c’est-à-dire celle de la nutation lunaire de 19 ans, n’étant que de 9" de chaque côté de la trajectoire moyenne de précession.
Les attractions des planètes, combinées avec le soleil et la lune, provoquent cependant un déplacement dans le plan de l’écliptique, de sorte qu’il oscille par rapport à l’équateur sur une longue période, variant de 26 000 ans à 53 000 ans, ce qui produit dans l’obliquité une série de maximum et de minimum, ayant une variation totale de 2º 37' 22", à savoir, d’un maximum absolu de 24º 35' 38 » à un minimum absolu de 21º 58' 36 », selon les calculs de Stockwell.
Il n’y a pas d’autres forces extérieures agissant sur la terre pour produire un changement supplémentaire dans l’obliquité de l’écliptique ; Mais on peut encore se demander s’il y a dans la terre elle-même des conditions internes qui peuvent affecter son mouvement. S’il y avait une irrégularité dans la distribution interne de la masse de la terre, provoquant un déplacement du centre de gravité par rapport au centre exact de la figure de la terre, cela produirait-il un changement dans l’obliquité ?
Dans un tel cas, « l’axe de figure » de la terre ne correspondrait pas exactement à « l’axe de révolution » de la terre, et il pourrait y avoir une inclinaison de l’un par rapport à l’autre. Il se produirait alors une oscillation, mais ce ne serait pas une oscillation de l’obliquité, mais une oscillation d’un autre genre, c’est-à-dire une « nutation eulérienne ». Il s’agit d’une oscillation corporelle de la figure terrestre autour de l’axe de rotation, qui reste fixe dans l’espace, de sorte que la position du pôle céleste (c’est-à-dire le point dans le ciel marquant le prolongement de l’axe de rotation de la terre) reste inchangée ; en d’autres termes, l’obliquité de l’écliptique n’est pas affectée au moindre degré par la « nutation eulérienne ».
Il y a, en fait, un tel mouvement de la terre, une « nutation eulérienne », mais d’une quantité excessivement petite. Elle est apparente dans les observations astronomiques comme une « variation de latitude ». La première preuve exacte de son existence a été obtenue en 1888, et depuis 1900, elle a été observée en permanence dans un certain nombre de stations de latitude internationales, spécialement choisies à cet effet.
Cette variation est irrégulière et si faible qu’elle est difficile à observer, étant toujours inférieure à 0,5 de la valeur moyenne. Cela représente un mouvement du pôle terrestre à moins de 50 pieds de sa position moyenne ; Et il n’y a aucune preuve d’un changement important de latitude à la surface de la Terre au cours des périodes historiques.
La possibilité d’une variation plus grande a été envisagée, et il a été démontré que, si l’on effectuait une déviation considérable de l’axe de figure de la Terre par rapport à l’axe de rotation, il se produirait alors une grande variation de latitude. Cette variation aurait une période de 305 jours si la terre était parfaitement rigide, mais de 432 jours dans son état actuel d’élasticité - c’est la période dérivée des observations internationales de latitude. De cette longue période, on a conclu que la terre, bien qu’elle ne soit pas parfaitement rigide, est cependant aussi rigide que l’acier.
De plus, il a été démontré par le professeur J.F. Twisden, en 1878, que si la variation de latitude était de grandes dimensions, « d’énormes mouvements de marée de l’océan se produiraient, et ses eaux balayeraient les continents à peu près comme une marée montante balaie un banc bas sur un rivage plat ». (J.F. Twisden. « Sur les déplacements possibles de l’axe de la Terre de la figure produit par les élévations et les dépressions de sa surface », Quarterly Journal of the Geological Society of London, vol. 34, 1878, p. 35, etc.)
Une telle marée n’existe pas, et la seule oscillation de marée observée, ayant une période d’environ 430 jours, est si minuscule qu’il n’est pas certain qu’un effet très léger de ce genre, apparemment observé par Bakhuysen en Hollande et Christie aux États-Unis, était dû à un accord accidentel ou non.
Outre les observations des marées, celles de la variation de latitude, ainsi que de la géodésie et de la sismologie, s’accordent toutes à montrer que la matière terrestre est disposée si symétriquement par rapport au centre de gravité de la terre et à son axe de rotation, qu’aucune grande nutation eulérienne n’est possible. De plus, comme nous l’avons indiqué plus haut, une telle nutation, même si elle existait, ne serait accompagnée d’aucun changement dans l’obliquité de l’écliptique.
Nous pouvons donc dire avec certitude que la variation de l’obliquité de l’écliptique, sous l’action de toutes les forces actuellement à l’œuvre, est parfaitement connue et a été calculée avec la plus grande précision ; de sorte que nous sommes obligés de rejeter toute suggestion selon laquelle la courbe des résidus de la figure 3 correspond à un mouvement périodique inconnu de la terre.
La conclusion ainsi tirée est que l’écart par rapport à la courbe théorique de l’obliquité est dû soit à des erreurs d’observation, soit à l’existence d’une anomalie d’un type inattendu.
Les pages qui suivent montrent que les erreurs d’observation sont tout à fait insuffisantes pour expliquer l’écart de plus en plus important lorsque la courbe est retracée jusqu’à l’Antiquité.
De plus, puisque la courbe elle-même est si clairement logarithmique, nous sommes limités à l’interprétation que cela implique. C’est-à-dire qu’à l’extrémité zéro, là où la courbe devient verticale, il y a « irrégularité », correspondant à une perturbation soudaine et majeure de l’axe de la terre ; Et à l’extrémité de 90º, là où la courbe devient horizontale, il y a « insensibilité », ou retour à l’équilibre.
En d’autres termes, il s’agit d’une courbe de récupération après une grande perturbation de l’axe de rotation de la terre, la perturbation s’étant produite en l’an 2345 av. J.-C., et le rétablissement de l’équilibre ayant été achevé en l’an 1850 après J.-C.
*********************
1. Connaissance des
Temps. 1827, p. 234. Retour
au texte
2. Smithsonian
Contributions to Knowledge, vol. 18, 1873, article 3, pp12,13. Retour
au texte
3. À l’exclusion
des observations chinoises, indiquées sur le graphique par un point
d’interrogation, puisque la date qui leur a été attribuée s’est avérée
manifestement erronée. Retour
au texte
4. H. Crabtree
« Tables tournantes et mouvement gyroscopique » 1909 . Chapitre 14, p. 124 . Retour
au texte
5. H. Crabree,
« Tables tournantes et mouvement gyroscopique », 1909. Chapitre 3, p. 47 ;
p.63. Retour au
texte
6. H. Crabtree, « Spinning
Tops and Gyroscopic Motion », 1909, p. 75. Retour
au texte
7. Le changement
que Manilius remarqua fut une diminution de près de 1/2 pouce de la longueur de
l’ombre au solstice d’hiver pendant la période de ses observations. Le
changement au solstice d’été était plus faible, mais toujours perceptible. Retour
au texte
**********************
note de Barry Setterfield : Dodwell a supposé ici que l’inclinaison originale de l’axe de la terre, avant 2345 av. J.-C., était presque verticale. Pour cette raison, il a supposé qu’un impact très fort était nécessaire pour secouer la terre de cette position à son inclinaison actuelle de 23,5 degrés. C’est pourquoi un certain nombre d’astronomes ont rejeté les travaux de Dodwell dans ce domaine. Cependant, si l’inclinaison de l’axe avait été supérieure à l’inclinaison actuelle de l’axe avant 2345 av. J.-C., il aurait fallu un impact beaucoup moins fort pour ramener la terre dans une position légèrement plus droite. La preuve de cette plus grande inclinaison de l’axe peut être vue dans les preuves de l’ère glaciaire qui couvrait la majeure partie de l’Europe avant 2345 av. J.-C.
Les travaux du Dr Benny Pieser du Cambridge Conference Group et du Dr Moe Mandelkehr ont montré qu’au cours de la période autour de 2345 av. J.-C., des changements climatiques, géologiques et archéologiques se sont produits au cours desquels certaines civilisations importantes ont été détruites - il semble que la première période intermédiaire en Égypte ait eu lieu à cette époque. Voir la conclusion pour une liste de références. Retour au texte.