
CHAPITRE 2
L’UTILISATION DU GNOMON DANS LES OBSERVATIONS ANTIQUES ET MÉDIÉVALES ; ET LES ERREURS D’OBSERVATION AVEC CET INSTRUMENT
[note des Setterfields : nous avons trouvé des illustrations des instruments mentionnés par Dodwell dans ce chapitre et les avons reliés en un groupe sous l’ensemble du texte afin de ne pas perturber le flux du texte lui-même. Après chaque série d’images pour chaque instrument, il y a un lien de retour « retour au texte » si vous souhaitez les voir pendant que vous lisez plutôt qu’après avoir terminé le chapitre. Ils sont liés à la PREMIÈRE fois que chaque instrument est mentionné.]
L’instrument le plus ancien, et celui qui est le plus fréquemment utilisé pour mesurer l’altitude du soleil à mi-journée aux solstices d’été et d’hiver, principalement dans le but de déterminer la date des solstices, était le gnomon ordinaire ou simple, qui était un pilier vertical, ou colonne, fixé sur une surface horizontale. La longueur de l’ombre projetée par le soleil a été mesurée, et à partir de là, l’altitude du soleil a été calculée.
« Pour faire les observations les plus considérables, les anciens et les modernes en ont fait un grand usage (le gnomon vertical), en particulier le premier, et beaucoup l’ont préféré aux quadrants plus petits, les deux parce qu’ils étaient plus précis, plus faciles à faire et plus faciles à appliquer. » Hutton, Dictionnaire philosophique et mathématique 1815. Vol. 1. Article, « Gnomon ».
Sur 85 observations, de 1100 av. J.-C. à 1650 apr. J.-C., l’ensemble des observations chinoises, et la grande majorité des autres, y compris les observations hindoues, grecques, arabes, perses et européennes médiévales, ont été faites avec le gnomon vertical. Dans de nombreux cas, lorsque d’autres instruments ont été utilisés, comme par les astronomes grecs à Alexandrie, et plus tard par certains observateurs européens arabes et médiévaux, ils étaient complémentaires au gnomon vertical, qui était également utilisé. C’est donc principalement sur les erreurs de cet instrument que notre attention est dirigée.
Une circonstance qui complique certaines observations est que les anciens observateurs ne corrigeaient pas leurs observations pour la réfraction, la parallaxe et le demi-diamètre du soleil. Cette dernière correction est nécessaire car le bord de l’ombre, projeté par le gnomon, correspond au bord supérieur du soleil, et non à son centre. Dans certains cas, cependant, au lieu que le gnomon ordinaire ou ordinaire projette une ombre, on en utilisait un avec une plaque de métal au sommet, percée d’un trou. Grâce à cela, le soleil projetait une tache circulaire de lumière sur la surface horizontale. Le centre de ce point de lumière a été mesuré et a donné l’angle, [qui] se rapportait correctement au centre du soleil.
Néanmoins, un résultat correct était possible avec le gnomon projetant des ombres si des solstices d’été et d’hiver étaient observés ; Parce que le vrai double angle d’obliquité est donné par l’observation du bord supérieur du soleil à ces deux occasions, affecté seulement légèrement par de très petites différences de réfraction. Cependant, lorsqu’un seul solstice a été observé, comme dans l’observation par Pythéas du solstice d’été à Marseille en 326 av. J.-C., il est nécessaire d’appliquer la correction du demi-diamètre du soleil à son observation enregistrée.
Très souvent, le rapport entre la hauteur du gnomon et la longueur de l’ombre, réduit, lorsque cela était possible, à des nombres entiers, ou à des nombres entiers et des fractions, était donné, de préférence à l’angle lui-même. Ainsi, Strabon, en parlant de la latitude d’Alexandrie, déterminée quand le soleil était sur l’équateur céleste, dit que : « À Alexandrie, le rapport du gnomon à l’ombre le jour de l’équinoxe est comme 5 à 3. »
C’est une coïncidence frappante que, lorsque la latitude d’Alexandrie est calculée à partir de ces chiffres, après avoir tenu compte de la réfraction, de la parallaxe et de la correction du bord du soleil vers le centre, nous obtenons la latitude exacte du musée d’Alexandrie, où les observations ont été faites, à savoir 31° 11' 42" N.
Pline (70 ap. J.-C.), dans son Histoire naturelle, livre II, chapitre 72, donne de même le rapport en nombres entiers pour Rome, car il dit qu’à Rome, au moment des équinoxes, l’ombre est au gnomon ce que 8 est au 9. De ce rapport, après avoir tenu compte de la réfraction, de la parallaxe et de la correction du bord du soleil vers le centre, nous obtenons pour la latitude de Rome 41º 52' 07 » N, ce qui n’est que 1' 26 » de moins que la latitude du Capitole à Rome.
Des nombres entiers avec une fraction, cependant, sont donnés par Strabon pour l’observation, faite par Pythéas, de l’ombre du soleil à midi au solstice d’été à Marseille vers 326 av. J.-C. Le rapport entre la hauteur du gnomon et la longueur de l’ombre est donné par Strabon comme 120 à 41 4/5. Ptolémée donne le rapport comme 60 à 20 5/6 ou 120 à 41 4/6.
À ce sujet, R.T. Gunther, dans son compte rendu de Ancient Surveying Instruments (Early Science in Oxford, Vol. 1, p. 330), dit : « Vers 326 av. J.-C., en préparation d’un voyage de découverte qui s’est terminé par la découverte de notre île de Bretagne, Pythéas a navigué de Phocée à Marseille. Là, il érigea un grand gnomon divisé en 120 parties, et fixa sa latitude avec un résultat qui semble presque incroyablement précis, pour appliquer le demi-diamètre du soleil, qu’il a omis, la latitude qu’il a obtenue ne diffère pas de plus d’une minute de la latitude réelle de l’observatoire de Marseille.
Ces résultats et beaucoup d’autres semblables provenant de sources chinoises et autres, par la précision substantielle des latitudes déterminées avec le gnomon vertical, témoignent abondamment que cet instrument, entre les mains d’observateurs expérimentés dans les temps anciens et médiévaux, était capable de donner des résultats proches de la vérité, lorsque certaines corrections, omises par les observateurs anciens, leur sont appliquées.
Il est intéressant ici, comme montrant la familiarité des anciens peuples avec l’utilisation du gnomon vertical, de mentionner son large utilisation à des fins domestiques et autres pour déterminer l’heure de la journée. Dans le Chariclès de Becker, illustrant la vie privée des Grecs de l’Antiquité, il est dit que le gnomon était, sans aucun doute, le moyen le plus ancien de mesurer l’heure du jour.
L’ombre qu’il projetait se mesurait en pieds. On en parle rarement, sauf en référence à l’heure du souper ou du bain. Pour le premier, on a attribué une ombre de dix ou douze pieds de long, et pour le second, on parle d’une ombre de six pieds. Il est donc probable que le gnomon était généralement construit de manière à projeter une ombre d’environ 12 pieds de long peu avant le coucher du soleil, car c’était l’heure à laquelle le souper, ou repas principal, avait généralement lieu. L’heure du bain était celle qui précédait le repas principal.
Dans Chariclès, dans une description d’un mariage, le soleil s’était couché à mi-chemin du méridien, tandis que les préparatifs se faisaient encore dans la maison des parents de la mariée. La mère, plus tard, prévient que le soir approche bientôt, et demande à une servante de s’assurer de l’heure : « Va, Ménododo, et mesure l’ombre sur le cadran solaire (gnomon) dans le jardin. » — Nous avons ici la clepsydre, interrompit Chloris : voyez combien d’eau il y a encore dedans ; il s’enfuira encore une fois avant le coucher du soleil. — Je suis sûr qu’elle a tort, dit Cléobule, il faut que ce soit plus tard. Mendora, cependant, revint avec l’assurance que l’ombre n’avait que huit pieds de long, et qu’il voulait donc encore un peu de temps pour se coucher.
D’après cet usage habituel et cette mesure de l’ombre du gnomon dans la vie civile ordinaire, nous pouvons être sûrs que, pour des raisons scientifiques, la longueur de l’ombre était soigneusement mesurée par les anciens astronomes.
L’observation la plus ancienne de l’inclinaison de l’axe de la terre, ou obliquité de l’écliptique, qui a été conservée, a été généralement attribuée au célèbre prince de la Chine, Chou Kung, frère de Wu Wang (fondateur de la dynastie Chou), qui est renommé en Chine à travers tous les siècles suivants pour sa sage législation et son intérêt pour la science astronomique. Il a été fabriqué à Loyang, dans la province de Honan, en Chine, vers 1100 av. J.-C. Cette observation a été faite avec un gnomon vertical, de 8 pieds de haut. Une hauteur de 8 pieds était la hauteur standard du gnomon en Chine, et cela a été fixé par la loi, en raison de la confusion causée par les différentes hauteurs des gnomons.
Le gnomon, sous différentes formes, remonte également à des temps très anciens en Égypte, même au 15ème siècle avant J.-C. De plus, les obélisques égyptiens, et même les grandes pyramides elles-mêmes, étaient, à des fins pratiques, essentiellement des gnomons à une échelle gigantesque. L’obélisque le plus ancien encore debout en Égypte (68 pieds de haut) est celui de Senusert Ier de la XIIe dynastie égyptienne à Héliopolis. Cela remonte à environ 2050 av. J.-C.
L’empereur romain Auguste, au début de l’ère chrétienne, a suivi l’exemple des Égyptiens en utilisant un obélisque de 75 pieds de haut, qu’il avait enlevé d’Héliopolis à Rome, « pour marquer les ombres projetées par le soleil ». Pline, qui mentionne ce fait, dit aussi que « Le nom d’obélisques signifie qu’ils sont sacrés au soleil ; C’est l’image des rayons du soleil que l’obélisque reproduit.
Cet obélisque a été érigé dans le Champ de Mars à Rome, et était l’un de ceux précédemment érigés par Psamtek Ier de la XXVIe dynastie égyptienne à Héliopolis. Il est maintenant situé sur le Monte Citorio, près de l’actuelle Maison du Parlement italien. Les ombres du soleil étaient projetées sur une pierre plate dont la taille correspondait à celle de l’obélisque. Ils ont été mesurés à l’aide d’une échelle de laiton, insérée dans la pierre, et la durée des jours et des nuits a été ainsi déterminée, en même temps que les solstices.
À mesure que le solstice d’été approchait, l’ombre de midi diminuait peu à peu, puis augmentait de nouveau ; et les effets opposés ont été observés au solstice d’hiver. Le mathématicien Manilius, afin d’obtenir des observations plus exactes, fixa au sommet de cet obélisque une boule dorée qui projetait une ombre circulaire noire et dense sur le pavé. Le centre de celui-ci pourrait être facilement et précisément mesuré. Cette forme de gnomon, à boule terminale, se retrouve sur les médailles de l’époque de Philippe de Macédoine (359 av. J.-C.) ; et cette disposition, qui était courante à Rome, est censée avoir été introduite en Grèce par Ménélas, roi de Sparte, vers 1180 av. J.-C.
Manilius ajouta ces paroles, à propos de ses mesures : « Cette observation, qui dure maintenant depuis près de 30 ans, n’est pas cohérente, ni à cause de la course discordante du soleil lui-même, et de quelque changement dans le ciel, ni à cause de quelque changement dans la terre universelle, par lequel elle s’est éloignée de son centre, comme je l’ai découvert moi-même, et j’en entends parler aussi en d’autres endroits. »
C’est une déclaration remarquable, et constitue la première reconnaissance d’un changement progressif de l’obliquité de l’écliptique. Il confirme également la précision que l’on peut obtenir avec le gnomon vertical, entre les mains d’un ancien observateur astronomique.
L’utilisation du gnomon s’est également répandue dans un passé lointain chez les astronomes de Chaldée ; et Hérodote dit que c’est des Chaldéens que les premiers astronomes grecs ont appris l’usage du gnomon et des polos. Le polo était un développement ultérieur du gnomon. C’était comme un bassin, au centre duquel se trouvait le bâton vertical, ou gnomon, sur lequel les douze heures du jour étaient marquées de lignes. L’altitude du soleil a également été mesurée avec lui.
Le gnomon, sous certaines de ses formes, était appelé par les Grecs un « skiotheron » (preneur d’ombres), ou « hélioptropion », c’est-à-dire un instrument pour indiquer la rotation du soleil aux solstices. Il était muni de marques de mesure et servait à montrer « les solstices, les temps, les saisons et l’équinoxe ».
Non seulement les Chinois et les Grecs, mais aussi les anciens hindous utilisaient également le gnomon à des fins similaires. Vitruve (environ 30 av. J.-C.) énumère plus de 10 formes différentes du gnomon ; et tandis que certains, utilisés comme cadrans solaires, étaient portables, d’autres atteignaient des dimensions considérables, jusqu’à 20 à 30 pieds de hauteur. Le plus haut gnomon, si l’on excepte les grandes pyramides d’Égypte, était celui d’Ulugh Beigh ; il a été utilisé à son observatoire à Samarcande en 1437 après JC, et mesurait 180 pieds de haut.
En plus du gnomon, des instruments circulaires étaient utilisés par les astronomes d’environ 300 av. J.-C., en particulier par les plus célèbres de ceux associés au musée d’Alexandrie, à savoir Timocharis, Eratosthène, Hipparque et Ptolémée.
C’étaient l’armille, l’astrolabe et le quadrant. L’armille et l’astrolabe ont été divisés en 360 degrés, et le quadrant en 90 degrés. On dit que les instruments plus grands de ce type étaient subdivisés à toutes les 10 minutes d’arc. Cela permettrait une mesure encore plus précise par estimation des fractions des subdivisions.
La forme la plus simple de l’armille consistait en un grand anneau de cuivre, gradué avec des degrés et des subdivisions, et monté verticalement dans le méridien. Un fil à plomb était utilisé pour assurer la verticalité. À l’intérieur, un second anneau tournait dans le même plan. Celui-ci portait deux broches diamétralement opposées, avec des pointeurs pour lire le cercle. L’altitude du soleil à midi a été mesurée en tournant l’anneau intérieur jusqu’à ce que l’ombre de la goupille supérieure tombe au centre de la goupille inférieure.
Il est clair que les astronomes grecs d’Alexandrie ne se sont pas limités à un seul instrument, mais en ont utilisé plusieurs qui étaient disponibles pour divers types d’observation. Il a été dit que « leur développement de la géométrie et de la trigonométrie, leur invention d’instruments bien conçus, et leur mesure et remesure des objets célestes, leur ont permis de tester leurs théories soigneusement formulées sur le système solaire ».
Bien que des instruments circulaires aient été utilisés à cette époque, permettant de lire directement les altitudes des corps célestes à partir de ces instruments, sans calcul, néanmoins, la très grande majorité des observations solaires de l’Antiquité ont été faites avec le gnomon vertical.
Ptolémée, connu sous le nom de « prince des astronomes », qui a fait des observations astronomiques à Alexandrie de 127 à 151 après J.-C., a inventé une amélioration notable du gnomon. C’était ce qu’on appelait l’Organon Parallactikon de Ptolémée, ou Regula Ptolemaica, plus tard appelé Règles de Ptolémée, ou Triquetrum.
Cet instrument était un poteau vertical, portant deux bras articulés. Le bras supérieur le plus court était articulé en haut du poteau. L’avant-bras le plus long était articulé à une distance du haut exactement égale à la longueur du bras supérieur. L’extrémité inférieure du bras glissait le long de l’avant-bras et portait un pointeur avec lequel on pouvait lire les marques d’échelle dans l’avant-bras. Cette disposition formait un triangle isocèle, dont les côtés égaux avaient tous deux 60 divisions de longueur ; les divisions d’échelle de la base permettaient d’obtenir très simplement l’angle au sommet à partir de la « table des accords » de Ptolémée.
Ptolémée a utilisé l’appareil pour mesurer la distance zénithale de la lune à Alexandrie. Un grand guidon pour prendre tout le disque de la lune, et un petit guidon, ont été utilisés. Gunther, en décrivant cet instrument, souligne que « dans les années qui ont suivi, avec l’instrument de Ptolémée, le Triquetrum, Copernic a fait les mesures avec lesquelles il a renversé le système ptolémaïque, et nous a donné une nouvelle idée de l’Univers ».
Le triquetrum utilisé par Copernic mesurait 8 pieds de hauteur. Il était fait de bois de pin et divisé par des marques d’encre, les deux bras égaux en 1000 parties, et la règle longue en 1414 parties. Pour illustrer l’exactitude de cet instrument, il faut mentionner que l’obliquité de l’écliptique obtenue à partir des observations faites par Copernic, après avoir tenu compte des corrections modernes pour la réfraction, etc., est à 23 secondes de l’arc, et celle qui est obtenue de la même manière à partir des observations de la lune par Ptolémée, est à 15 secondes de l’arc de la valeur vraie.
Bien que les anciens astronomes n’aient mesuré que la longueur de l’ombre projetée par le gnomon et calculé l’altitude du soleil sans corriger la réfraction, la parallaxe ou le demi-diamètre du soleil, ils ont néanmoins pris grand soin de s’assurer de la verticalité du gnomon et de l’horizontalité de la surface sur laquelle l’ombre tombait. Ils mesurent également la longueur de l’ombre avec une précision considérable.
Il est facile d’appliquer les corrections qu’ils ont omises ; et l’exactitude substantielle de la latitude, qui est ensuite dérivée de leurs observations, prouve que leurs observations solaires n’ont pas été affectées par des erreurs grossières, comme on l’a parfois supposé, mais qu’elles sont d’un ordre d’exactitude plus élevé qu’on ne l’a généralement admis.
Considérons maintenant les moyens qu’ils ont employés pour obtenir les meilleurs résultats de leur instrument standard, le gnomon.
En premier lieu, la verticalité était affectée par l’utilisation du fil à plomb, qui était un accessoire bien connu utilisé dans les observations astronomiques anciennes. Le Dr Breasted décrit le « Merkhet » égyptien, utilisé pour orienter les temples à partir d’avant 2000 av. J.-C., et au-delà. Il se composait d’une girouette faite à partir de la nervure centrale d’une feuille de palmier et d’un fil à plomb suspendu à un support en ivoire. On sait aussi que dans les archives stellaires des tombes appartenant à la XXe dynastie en Égypte, un observateur est représenté faisant une observation astronomique avec un instrument muni d’un fil à plomb.
Le
fil à plomb, maintenu tendu par un petit plomb de plomb, remonte donc
aux temps les plus anciens. Dans la description de l’Astrolabe de
Ptolémée, il est dit que « lorsqu’une observation était faite,
l’instrument était maintenu à la verticale par un fil à plomb ».
Cette pratique s’est poursuivie jusqu’à l’époque médiévale, et des
images d’instruments astronomiques médiévaux sont fréquemment montrées
avec le fil à plomb et le fil à plomb attachés.
En Chine, le livre classique d’astronomie le plus ancien, le Chou Pei, dont certaines parties remontent à 1100 av. J.-C., ne mentionne pas l’utilisation d’un fil à plomb, mais des instructions sont données pour installer le gnomon (Pei) en cercle (Chou), dans lequel, après avoir nivelé la surface sur laquelle l’ombre tombe, un carré est utilisé pour établir la verticalité du gnomon.
L’équerre avait ses côtés dans le rapport de 3, 4, 5, ou mieux 6, 8, 10, dans lequel 8 pieds est la hauteur du gnomon, 6 pieds la base du triangle rectangle et 10 pieds son hypoténuse. La mise en place du gnomon et son utilisation en observation étaient supervisées par un officier appelé le Ta-Tsiang (Grand Charpentier).
L’astronome français E. Biot, qui traduisit le Chou Pei en une traduction française en 1841, commente :
"Nous trouvons ici une mention irréfutable de la propriété fondamentale du triangle rectangle, connue parmi nous sous le nom de Théorème du carré de l’hypoténuse ...... elle est tout à fait remarquable par sa priorité de six siècles avant la découverte par Pythagore.
Il souligne également que le Chou Pei « se réfère en termes exprès au gnomon avec un trou, (qui produit une image circulaire du soleil, à la place du bord d’ombre projeté par le gnomon ordinaire ou simple). Ceci, jusqu’à présent, a passé pour avoir été introduit en Chine par les Arabes vers le XIIIe siècle de notre ère. Ainsi, nous voyons que, comme dans le cas de la boussole magnétique, les anciens Chinois ont ouvert la voie bien des siècles avant que les progrès européens de la science n’aient lieu. L’introduction du gnomon à trous, d’après les indications du texte du Chou Pei et la date des commentateurs, serait postérieure de plusieurs siècles à l’époque de Chou Kung, et peut-être dès le IVe ou le Ve siècle av. J.-C., bien que le gnomon à sommet plat ait été plus couramment employé.
Les astronomes arabes du Moyen Âge ont donné les règles suivantes pour assurer la verticalité des gnomons qu’ils utilisaient : (1)
Afin d’obtenir des lignes et des surfaces horizontales, les anciens astronomes utilisaient l’eau dans des récipients de différentes dimensions. Ainsi : « C’est en versant de l’eau dans de grandes cavités de faible profondeur, que les Égyptiens ont réussi à donner une horizontalité parfaite à la base de leurs pyramides. » (2) Il est dit que lorsque les anciens observateurs préparaient une surface plane pour la mise en place d’un gnomon, « la surface du sol était aplatie et nivelée jusqu’à ce que l’eau versée dessus s’écoule également de tous les côtés ». (3)
Une méthode similaire a été utilisée par les anciens astronomes hindous, comme décrit dans le Surya Siddhanta. L’ancien observatoire hindou..... « se composait principalement d’un plan horizontal nivelé, d’un sol ou d’une terrasse de Chunam, qui est une chaux faite de coquillages, et qui, une fois sèche, est dure et capable de recevoir un polissage égal à celui du marbre. Sur la surface de ce sol de chunam, nivelé par l’eau, un cercle est décrit, et une tige verticale de longueur donnée est érigée au centre, comme un style ou un gnomon, et au moyen de la longueur et de la direction de son ombre projetée sur le plan par le soleil, une variété de problèmes astronomiques sont résolus. (4)
Vitruve (63 à 14 av. J.-C.) a décrit à la fois les « aquariums de la
balance » (niveaux d’eau) et les « chorobates ». Ce dernier était le
type le plus simple, consistant en "une longue auge ou un canal en
bois ; qui, étant également rempli d’eau, sa surface montre la ligne de
niveau. (5)
En
Chine, un gnomon de 8 pieds de haut est décrit par Du Halde, à Pékin,
qui projetait une ombre sur une table, ayant une plaque de laiton au
milieu, sur laquelle était tracée une ligne méridienne de 15 pieds de
long. « Tout autour de la table, il y a de petits canaux pour recevoir
l’eau, par lesquels elle doit être nivelée. » (6)
Il s’agissait évidemment d’un procédé conforme à l’ancienne pratique en
Chine.
Chez les Arabes, il est mentionné dans l’Encyclopédie de l’Islam (Houtsma, vol. III, page 535, article Al-Mizan), que les astronomes arabes ont certainement adopté un grand nombre de méthodes de nivellement et de test des niveaux, chez d’autres peuples, soit les Byzantins, soit les Perses. Les déclarations sur la construction des canaux, etc., concordent avec celles de Vitruve, qui à son tour s’est appuyé sur des sources grecques. Les Arabes ont appris en partie des travaux grecs, mais ils ont également utilisé des données acquises par l’expérience pratique.
Pour examiner si la surface était parfaitement horizontale, les tests suivants ont été adoptés :
Erreurs des observations anciennes
Nous pouvons maintenant entrer dans la question des erreurs d’observation associées à ces anciens instruments et méthodes par lesquels l’obliquité de l’écliptique a été trouvée. Ceci est d’une grande importance dans la présente étude, parce que de grandes erreurs, si elles existaient dans les observations anciennes, seraient le seul motif astronomique valable d’objection aux conclusions qui en découlent.
Si les observations anciennes étaient si erronées qu’elles étaient complètement non fiables, alors nous serions en train de suivre un faux indice, nous éloignant de la vérité. Si, d’un autre côté, ces anciennes observations sont, en général, fiables dans des limites d’erreur relativement petites, alors la vérité qu’elles établissent pourrait bien être de la plus haute importance et nous conduire à de nouvelles perspectives concernant le mystère de la vie de l’homme sur la terre.
Toute autre objection astronomique, telle que la suggestion qu’une sorte de courbe, autre qu’une courbe de récupération d’une perturbation de l’axe de la terre, pourrait également correspondre aux observations, sera jugée insoutenable. Car une telle suggestion est exclue par le fait que les forces du soleil, de la lune et des planètes, agissant sur la terre au cours des âges passés de la même manière qu’aujourd’hui, expliquent pleinement l’ensemble du mouvement cyclique normal de l’axe de la terre. Ces forces, et leurs effets, sont bien connus et ont été calculés avec précision.
Il n’y a donc pas de place pour tout autre mouvement harmonique de l’axe de la terre. Nous sommes, en fait, limités à ces forces, parce qu’un mouvement d’une ampleur appréciable, dû à des changements internes à l’intérieur de la terre, ou à une différence quelconque entre le centre de gravité de la terre et son centre de figure, deviendrait immédiatement apparent comme une oscillation « eulérienne », comme nous l’avons déjà indiqué. Elle serait observable comme une « variation de latitude », et non comme un changement dans l’inclinaison axiale de la Terre. Nous avons vu que cette variation de latitude existe en effet à l’heure actuelle, mais seulement sur une échelle extrêmement petite.
Par conséquent, quelle que soit l’amplitude de la différence entre la courbe de récupération et ses implications et les croyances actuelles, tant en géologie qu’en astronomie, il faut nécessairement en tenir compte, à moins que la différence sans cesse croissante entre ces observations anciennes et la courbe normale de l’obliquité, à mesure que nous la remontons dans les âges passés, puisse être attribuée à juste titre à des erreurs des observations anciennes.
Nous sommes donc arrivés au cœur du problème. C’est le terrain d’essai sur lequel de nombreuses conclusions de grande portée doivent se tenir ou tomber. Pour cette raison, une attention considérable a été accordée dans les pages précédentes à la description de l’instrument principal, c’est-à-dire le gnomon vertical utilisé dans les temps anciens.
Les
erreurs d’observation peuvent maintenant être considérées d’abord à
l’égard de la nature et de la quantité des erreurs particulières à
l’instrument lui-même ; et deuxièmement, la lumière est également jetée
sur ces erreurs par des preuves internes, dans de nombreux cas contenues
dans les observations anciennes, en différents lieux et à différentes
époques. D’un point de vue astronomique, il n’y a rien de difficile à
cela ; et le lecteur général sera facilement en mesure de se faire sa
propre opinion sur la question à partir des données qui vont maintenant
être présentées.
Il y avait quatre sources principales d’erreur, en fonction de
l’instrument et de ses accessoires. Ces erreurs instrumentales étaient
liées à :
Une cinquième source d’erreur devrait également être prise en compte si
le gnomon, au lieu d’être à sommet plat, avait un sommet pyramidal.
Il est certain, cependant, qu’à l’exception peut-être de certaines des premières observations arabes entre 800 et 900 après J.-C., dans tous les autres cas où un gnomon a été utilisé, il s’agissait soit d’un gnomon à sommet plat, soit d’un gnomon avec un trou au sommet, donnant une image circulaire du soleil, dont le centre a été mesuré. Nous y reviendrons un peu plus loin.
En ce qui concerne la première source d’erreur, liée à l’échelle de mesure, nous ne pouvons douter que les échelles linéaires finement divisées n’aient été utilisées dans l’Égypte ancienne. La merveilleuse architecture égyptienne, dans ses dimensions colossales, montre que les dessins architecturaux ont dû être réalisés avec des instruments de dessin exacts, nécessitant des échelles fines pour la mesure linéaire.
La puissance d’estimer avec précision de petites fractions de divisions linéaires est également indiquée par « la perfection du dessin égyptien et de la science de la forme », mentionnée par J. Capart, « dans le dessin mural des tombes des rois à Thèbes ». L’artiste commence par dessiner un système de carrés très précis. « Des lignes horizontales et verticales formaient un véritable réseau pour guider la main et l’œil dans le déroulement du travail. » (7)
Les grandes réalisations artistiques, tant chez les anciens Égyptiens que chez leurs successeurs grecs, ont dû nécessairement être associées à une perception aiguë de la fine subdivision linéaire.
Sir Flinders Petrie dit, à propos des pierres d’enveloppe de la Grande Pyramide, que ces pierres ont été travaillées avec une précision égale à celle du meilleur travail d’opticien, étant lisses et droites jusqu’au centième de pouce sur une longueur de 75 pouces, et qu’elles ont été assemblées avec du plâtre de ciment de Paris à des joints presque imperceptibles de seulement deux centièmes de pouce d’épaisseur. Une telle précision implique que les Égyptiens avaient atteint une haute perfection dans l’art de la mesure linéaire. Antoniadi exprime également l’opinion que « la coudée égyptienne était divisée en centièmes avec des subdivisions très fines, comparables à notre millimètre ». (8)
La preuve d’une précision similaire dans un département de mesure similaire est contenue dans l’affirmation que « les anciens Égyptiens mesuraient également des poids à la décimale d’un grain ». Nous pouvons conclure sans risque de se tromper que, dans les mesures astronomiques, à l’époque des astronomes alexandrins, l’erreur introduite par l’utilisation d’échelles linéaires serait très faible.
Dans la Chine ancienne, le gnomon standard mesurait 8 pieds chinois. Le pied chinois (Chih) était légèrement plus long que le pied anglais et équivalait à 13,32 pouces anglais. Le gnomon lui-même avait donc 8 pieds 9 pouces de haut, exprimé en mesure anglaise.
Les Chinois ont adopté des subdivisions décimales. Un dixième de pied chinois s’appelait un Tsuen (correspondant à notre pouce). Il s’agissait donc de 1,3 pouce anglais. Celle-ci a été subdivisée en dixièmes, ou fen, correspondant à 0,13 pouce anglais, soit pratiquement 1/8 de notre pouce. P. Gaubil, qui a extrait de nombreuses longueurs d’ombre solstitielles des anciens documents chinois, donne ces longueurs d’ombre mesurées en pieds chinois en pouces et en fen, c’est-à-dire qu’ils ont mesuré l’ombre au 1/8 de pouce anglais le plus proche. Ainsi, l’erreur de mesure de l’ombre, dans la mesure où elle dépendait de l’échelle linéaire, n’excédait pas la moitié de cette quantité, c’est-à-dire 1/16 de pouce anglais.
Dans leur système de mesure linéaire, les Chinois subdivisaient en outre le fen en 10 li, et le li en 10 hao. Nous voyons donc que les anciens Chinois utilisaient des mesures à l’échelle fine.
Dans leurs mesures circulaires, le cercle standard avait une circonférence de 365 1/4 degrés, soit le même nombre de jours dans l’année. Ainsi, ils ont adopté le cercle standard de l’année-jour, qui était également la base du système de mesure de l’Égypte ancienne ; c’est aussi une caractéristique intéressante de l’ancien monument circulaire britannique de Stonehenge.
Dans le Chou Pei, des instructions sont données pour niveler le sol sur un diamètre de 126 pieds, et pour « effectuer le processus de nivellement avec le niveau de l’eau ». Sur cette plate-forme nivelée, un cercle est tracé de 365 1/4 pieds de circonférence. Le cercle doit être divisé avec soin en ce nombre de degrés. L’instruction est donnée : « Qu’il n’y ait pas la plus petite différence entre les degrés. »
Le cercle est ensuite divisé en 4 quadrants, en étirant un fil exactement du nord au sud, et un autre transversal à celui-ci, d’est en ouest. Chacune des quatre parties de la circonférence, dit-on, embrassera 91 5/16 degrés.
Au centre de ce cercle étendard, un gnomon est érigé, de 8 pieds chinois de hauteur, et le Chou Pei procède ensuite avec des instructions pour faire des observations astronomiques avec lui. En plus de diviser le cercle standard en 365 1/4 degrés, il a également été divisé en 714 000 li circulaires, chacune de ces petites divisions équivalant à 0,536 li linéaire.
On en dit assez pour montrer clairement que les anciens Chinois étaient extrêmement prudents avec les mesures linéaires et circulaires à petite échelle. L’erreur maximale de cette source serait d’un demi-« fen », ce qui équivaut à 1/16 de pouce (en anglais). Cela introduirait dans la mesure de l’obliquité, pour les observations aux deux solstices, la possibilité d’une erreur maximale de seulement 1 1/3 minute d’arc. Celle-ci serait réduite à une quantité négligeable dans un résultat dépendant de plusieurs observations.
Erreur de verticalité du gnomon
Comme le gnomon a été rendu vertical au moyen d’un fil à plomb, toute erreur de verticalité proviendrait d’un manque de parallélisme entre le fil à plomb et le gnomon. Une détermination expérimentale montre que cela ne provoquerait qu’une erreur d’environ une demi-minute d’arc dans l’altitude observée du soleil.
Des expériences avec le niveau de l’eau montrent qu’il est possible d’obtenir l’égalité du niveau de l’eau sur deux côtés opposés d’une surface nivelée à l’intérieur d’un vingt-cinquième de pouce. Avec le gnomon, cela donne une erreur d’environ une minute d’arc dans l’altitude du soleil.
Le problème de la mesure du bord de l’ombre peut sembler à première vue introduire une incertitude considérable ; et les écrivains modernes attribuent souvent une proportion considérable des erreurs supposées des anciennes observations astronomiques à une difficulté à observer le bord de l’ombre solaire.
Cette difficulté n’est pas aussi grande qu’on l’a suggéré. Au bord de l’ombre projetée par un simple gnomon, il y a un point reconnaissable où un léger flou devient appréciable ; À partir de ce point, la pénombre s’affaiblit rapidement jusqu’à ce qu’elle se perde en pleine illumination. L’expérience montre que le point où commence le flou de l’ombre, qui est reconnu par les observateurs comme le « bord de l’ombre », correspond à un petit segment de près d’un dixième du diamètre solaire, apparaissant juste au-dessus du gnomon.
Cependant, afin d’examiner les erreurs de telles mesures, le meilleur moyen semble être l’observation expérimentale réelle, faite dans des conditions similaires à celles des observations anciennes ; c’est-à-dire avec un gnomon dont la verticalité est testée au moyen d’un fil à plomb, et dont la surface horizontale sur laquelle tombe l’ombre est nivelée par un niveau d’eau. Ces expériences mettent alors en lumière non seulement les erreurs de mesure du bord de l’ombre, mais aussi les erreurs dues au fil à plomb et au niveau.
Tests à l’Université d’Adélaïde
Cette méthode pratique pour tester les erreurs du gnomon a été utilisée à Adélaïde au solstice d’hiver en juin 1936. Un gnomon vertical a été construit à l’observatoire d’Adélaïde, à l’aide d’un morceau de bois de pin de 6 pieds de haut, vissé à une planche de mesure horizontale de 10 pieds 6 pouces de long. Un fil à plomb a été utilisé pour rendre le gnomon vertical, et la planche de mesure a été nivelée avec un niveau d’eau.
Trois types de mesures ont été effectuées :
Ce
gnomon a été installé le 12 juin 1936 dans l’un des grands cadres de
fenêtre du département de physique de l’Université d’Adélaïde, et une
longue série d’observations a été faite à laquelle 9 observateurs ont
participé. Le bord de l’ombre s’est avéré être beaucoup plus clairement
défini qu’on ne l’avait prévu, même lorsque sa plus grande longueur a
été atteinte, au solstice d’hiver.
Afin de tester les résultats avec un gnomon plus élevé, projetant une
ombre plus longue et moins bien définie, une série d’observations a
également été faite en utilisant comme gnomon le bord d’une planche
fixée à la tour d’arpentage de l’université, à une hauteur de 30 pieds
au-dessus du sol. L’ombre était reçue et mesurée sur une longue planche
de niveau, posée sur le sol et maintenue horizontale au moyen d’un
niveau d’eau. Le point zéro pour les mesures de l’ombre a été pris à
partir du centre d’une cheville enfoncée dans le sol, et trouvé au moyen
d’un fil à plomb être verticalement sous le bord de la planche de gnomon
projetant des ombres. Les distances horizontales entre la cheville et le
bord de l’ombre ont été mesurées à l’aide d’un ruban à mesurer
d’arpenteur, indiquant au huitième ou au quart de pouce le plus proche.
Ces mesures horizontales étaient généralement assez constantes à un
quart de pouce ou moins.
Avec un petit gnomon de 6 pieds, les mesures horizontales ont été faites à l’échelle du millimètre, et la cohérence de la mesure du bord de l’ombre était de 1 à 2 millimètres, c’est-à-dire de 1/25 à 1/12 de pouce. Cela suffit pour indiquer que, avec un gnomon de 8 pieds 9 pouces de hauteur, correspondant à 8 pieds chinois, le bord de l’ombre pourrait facilement être mesuré à 2 à 3 millimètres près, ce qui correspond à un peu moins de 1 « fen » chinois.
Ainsi, les enregistrements chinois de la longueur des ombres aux solstices, donnés en Chih (pieds), tsuens (pouces) et fen (dixièmes de pouce chinois), peuvent être considérés comme des mesures fiables des ombres solstitielles selon les échelles linéaires utilisées par les anciens astronomes chinois. Dans les observations d’Adélaïde, le point marqué par le fil à plomb comme le zéro pour les mesures horizontales a été facilement déterminé à 1 millimètre près.
À partir de ces données, il est possible de calculer les erreurs d’altitude observée du soleil, dues à ces trois sources – mesure du bord de l’ombre, verticalité et niveau. Dans le pire des cas, lorsque les erreurs s’accumulent toutes dans la même direction, elles produisent une erreur maximale de 2',6 au-dessus ou au-dessous de l’altitude moyenne réelle du soleil. La différence entre l’altitude la plus élevée et l’altitude la plus basse serait alors de 5'.2.
Un calcul similaire des erreurs au solstice d’été donne le même résultat qu’au solstice d’hiver. La pire observation peut être de 2'.6 au-dessus ou au-dessous de l’altitude vraie du soleil, et la plage de l’observation la plus haute à l’observation la plus basse peut s’élever à 5'.2 .
Au solstice d’hiver de juin 1936, 172 observations de la bordure d’ombre ont été faites par 9 observateurs. La moyenne des 172 observations montre que l’altitude observée du bord supérieur du soleil obtenue avec le gnomon simple nécessite une réduction de 13'. 2 afin d’obtenir l’altitude du centre du soleil. L’observation la plus élevée était de 15'.3 (c’est-à-dire 2'.1 au-dessus de cette valeur moyenne), et la plus basse était de 10'.4 (c’est-à-dire 2'.9 en dessous de la valeur moyenne).
L’amplitude extrême était donc de 4'.9 et la moyenne des lectures les plus hautes et les plus basses était de 12'.85, c’est-à-dire à seulement 1/3 de minute de la moyenne de l’ensemble des 172 observations. Ces résultats montrent la précision substantielle qu’il est possible d’obtenir avec une longue série d’observations avec le gnomon.
Cent soixante et onze observations de la tache d’ombre circulaire, projetée par la boule, ont donné le vrai centre du soleil à 0',4, l’altitude observée étant de ce point légèrement inférieure au vrai centre du soleil. L’explication de cela est dans une certaine mesure liée au fait que l’ombre de la balle, telle qu’elle est projetée sur une surface horizontale, n’est pas un vrai cercle, mais est légèrement elliptique dans la direction de sa longueur. Le centre estimé de cette ombre elliptique donne la longueur [qui est] très légèrement trop grande. On observe donc que l’altitude du soleil est juste un peu plus petite que l’altitude réelle.
La lecture la plus élevée de la tache d’ombre circulaire était de 1',7 au-dessus du résultat moyen, et la plus basse était de 2',4 au-dessous de celui-ci ; de sorte que la portée était de 4',1, un peu moins que dans le cas des observations du bord de l’ombre.
Les observations avec le gnomon de 30 pieds au sommet de la tour d’étude de l’Université ont donné la même correction que celle donnée par le petit gnomon, à savoir 13'.2, pour réduire l’altitude observée du bord supérieur du soleil à son centre. La portée, de la lecture la plus élevée à la plus basse, 4'.1, était légèrement plus petite pour le gnomon de 30 pieds que pour le gnomon de 6 pieds. Cet avantage du gnomon plus élevé s’explique par la précision relativement plus grande des corrections verticales et de niveau.
Les
résultats obtenus avec le gnomon de 6 pieds, confirmant la portée
calculée avec cet instrument d’environ 5', sont d’un intérêt particulier
si l’on considère l’affirmation de Ptolémée selon laquelle les
observations d’Eratosthène à Alexandrie ont donné une valeur pour
l’angle de double obliquité « supérieure à 47° 40' mais inférieure à 47°
45', de sorte qu’en prenant la moyenne, il l’a faite 47° 42' 30 », cette
proportion est à l’ensemble du cercle comme 11 à 83, exactement comme le
dit Eratosthène lui-même. À partir de là, il a défini l’obliquité
maximale du soleil comme 23° 51' 19 ». » (10)
Nous voyons par cette affirmation qu’il y avait une différence de 5
minutes d’arc entre les résultats extrêmes obtenus par Ératosthène.
C’est exactement la même différence calculée et observée obtenue avec le
gnomon de 6 pieds à Adélaïde.
D’après les déclarations des écrivains anciens, il est clair qu’Eratosthène utilisait un gnomon pour ses observations solstitielles du soleil, ainsi qu’une armille, qui était complémentaire au gnomon. Il est également clair que les résultats donnés par Ératosthène ont été obtenus à partir d’une série d’observations aux solstices d’été et d’hiver, car Ératosthène a vécu 40 ans à Alexandrie, période pendant laquelle il a effectué ses travaux astronomiques historiques, y compris la célèbre mesure de la circonférence de la terre.
Ces
considérations sont une vérification complète et frappante de
l’exactitude de la valeur moyenne de l’obliquité de l’écliptique obtenue
par Ératosthène.
Les observations faites avec des plaques métalliques triangulaires,
fixées au sommet du gnomon, avec des angles différents au sommet,
étaient en parfait accord avec la géométrie de ce type de gnomon. Les
angles au sommet ont été variés de manière à correspondre aux obélisques
et aux pyramides égyptiennes, ou aux gnomons à sommet conique utilisés
par certains des premiers astronomes arabes vers 800 après J.-C.
Dans tous les cas, le gnomon à sommet triangulaire donne une ombre plus courte que le gnomon uni ou à sommet droit. Au solstice d’hiver, un gnomon avec un angle de sommet de 90° nécessite une correction (à l’altitude observée du soleil pour obtenir son centre) de 17'.5 au lieu de 13'.2. Avec un angle apex de 60°, la correction est de 23'.7 ; avec 30°, c’est 44'.1 ; et avec un angle très aigu de 20°, il est de 65'.0.
Cependant, aucun des documents anciens n’a été obtenu avec des gnomons à angles aigus. Toutes, à l’exception de quelques-unes des observations arabes, ont été obtenues avec le gnomon ordinaire à sommet plat ou plat, ou dans quelques cas, avec un gnomon ayant un trou central au sommet.
Un gnomon à angle aigu donnerait une valeur trop petite pour l’obliquité. Ce qui est frappant, cependant, à propos des observations anciennes (à l’exception de quelques-unes faites par les premiers Arabes), c’est qu’elles donnent une plus grande valeur à l’obliquité qu’à la valeur théorique, et la différence augmente considérablement à mesure que nous remontons aux observations les plus anciennes. Le test de leur exactitude réside non seulement dans l’investigation pratique qui précède, mais aussi dans les valeurs remarquablement précises de latitude que donnent les anciennes observations.
En résumant les preuves, on peut donc dire que lorsque la question des erreurs, auxquelles étaient susceptibles les anciennes observations de l’obliquité de l’écliptique, est soumise à un test expérimental pratique, en utilisant des instruments et des méthodes correspondant à ceux des temps anciens, les résultats confirment l’exactitude des observations dans une ou deux minutes d’arc, et montrer que, dans une longue série d’observations de ce genre faites par un observateur attentif, il ne se produit pas de grandes erreurs.
Ceci est d’une grande importance, compte tenu des conclusions de grande portée tirées des observations anciennes, et démontre que ces conclusions sont fondées sur des faits d’observation.
***********************
Chapitre 2 Illustrations -- Retour au début du chapitre 2
Le Gnomon (quatre illustrations ci-dessous)
Ce gnomon est en Chine aujourd’hui

http://hua.umf.maine.edu/China/astronomy/tianimage/0022MingGnomon6471w.jpg
Ce gnomon provient de l’Égypte ancienne et s’appelle « l’aiguille de Cléopâtre ». Celui-ci est à New York aujourd’hui. Trois existent dans le monde d’aujourd’hui et peuvent être trouvés à Londres, Paris et New York. Ils sont mal nommés car ils n’ont aucun lien avec la dame, mais existaient depuis environ mille ans au moment où elle vivait.

http://www.milesfaster.co.uk/information/london-attractions/images/cleopatras-needle.jpg
Les deux illustrations suivantes sont du gnomon appelé Cadran solaire d’Auguste. Auguste l’a fait expédier à Rome depuis l’Égypte après avoir conquis l’Égypte en 31 av. J.-C.
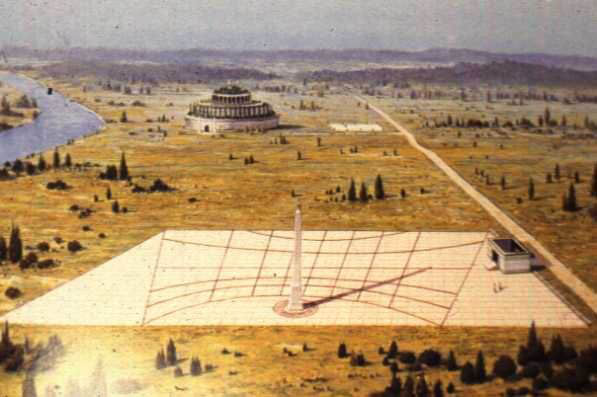
ttp://www.italiannotebook.com/images/sundial3.jpg

http://www.vroma.org/images/mcmanus_images/ara_horologium.jpg
L’Armilla (deux illustrations ci-dessous)
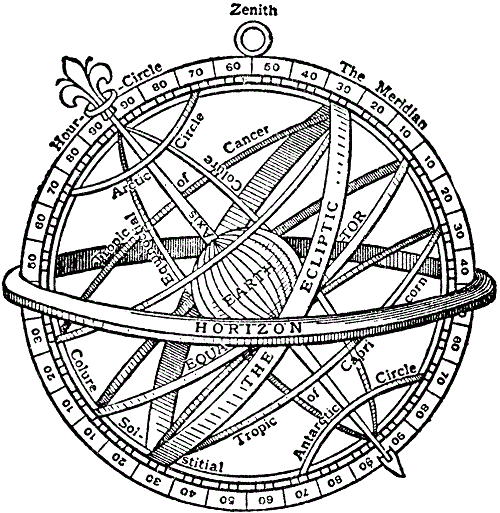
http://etc.usf.edu/clipart/27800/27809/armilla_27809_lg.gif
une grande armille équitoriale

http://hua.umf.maine.edu/China/astronomy/tianimage/0034EquatorialArmilla6499w.jpg
Astrolabe (deux illustrations ci-dessous)

http://www.eac.edu/events/images/astrolabe.jpg
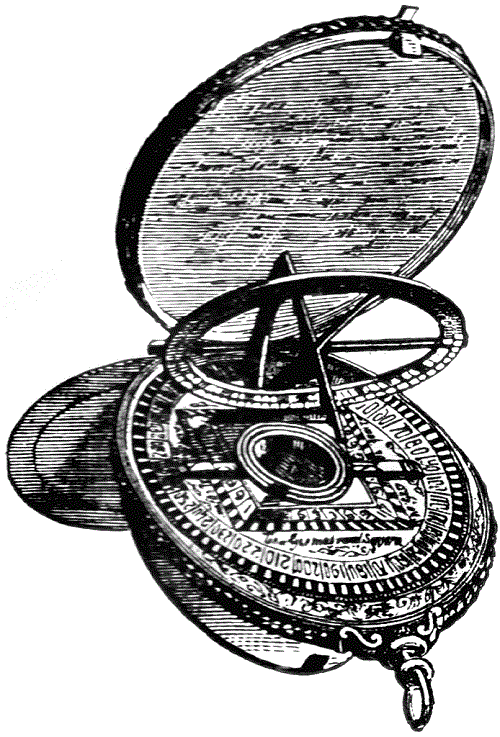
http://etc.usf.edu/clipart/15500/15592/astrolabe_15592_lg.gif
Quadrant (deux illustrations ci-dessous)

http://www.mat.uc.pt/~helios/Mestre/Novemb00/H61iflan.htm

http://www.aip.org/history/cosmology/tools/images-tools/quadrant52002m.jpg
Triquetrum

http://idacdonikad2.blox.pl/resource/Triquetrum1.jpg