CHAPITRE 5
OBSERVATIONS DE LA GRÈCE ANTIQUE
Ces observations sont l’œuvre d’une galaxie d’astronomes célèbres de l’Antiquité, à savoir Thalès, Pythéas, Hipparque, Ératosthène et Ptolémée.
La plus ancienne observation grecque enregistrée de l’obliquité de l’écliptique est celle de Thalès de Milet en 558 av. J.-C. Milet était une ville importante sur la côte sud-ouest de l’Asie Mineure, à 53 miles au sud de Smyrne. Thalès était « le premier des sept Sages de la Grèce ». Il fut autodidacte jusqu’à ce qu’il se rende en Égypte, où il interviewa les prêtres-astronomes d’Égypte et, dit-on, apprit la géométrie des Égyptiens.
Plutarque décrit comment ce philosophe a pu mesurer la hauteur des pyramides en utilisant uniquement sa canne. « N’ayant besoin d’aucun instrument, mais levant votre canne à l’extrémité de l’ombre produite par la pyramide, vous avez formé deux triangles au point où les rayons solaires se rencontraient, montrant ainsi la proportion entre les deux ombres et entre la pyramide et la canne. » D’autres auteurs disent que cette mesure a été faite lorsque le soleil était à une altitude de 45 degrés.
On dit que Thalès a prédit l’éclipse solaire totale de 584 av. J.-C., qui est donc entrée dans l’histoire sous le nom d'« éclipse de Thalès ». Les Lydiens et les Mèdes, qui étaient en guerre les uns contre les autres et qui livraient bataille, selon le récit d’Hérodote, « quand ils virent venir la nuit au lieu du jour, cessèrent de combattre, et les deux partis furent plus désireux de faire la paix l’un avec l’autre ».
Pour l’observation de l’obliquité de l’écliptique, il est évident que Thalès utilisait un gnomon, car cet instrument avait été utilisé chez les Babyloniens bien avant son temps. Anaximandre, qui était un contemporain de Thalès, et qui était aussi un philosophe de l’école ionienne, est crédité d’avoir introduit l’utilisation du gnomon chez les Grecs.
Wendelin, dans son Solis Obliquitas, dit de cette observation :
À l’époque des rois Cyrus et Crésus, lorsque Thalès le Milésien prospéra et donna les premiers rudiments de l’astronomie aux Grecs, il définissait l’intervalle entre les deux tropiques comme étant de 8 parties sur 60 de l’ensemble du cercle. À partir de là, nous trouvons l’intervalle de 48°, lorsque nous divisons le cercle en 360°, de sorte que l’obliquité maximale du soleil était de 24 degrés entiers.
Messala, dans L’Astrolabe, discutant du changement de l’obliquité du soleil à diverses époques, déclare que cette même valeur de 24° était autrefois donnée par les Hindous dans leurs écrits. L’époque où Thalès a prospéré était lors de la 55e olympiade, c’est-à-dire 558 avant notre ère.
Nous avons vu la confirmation de cette remarque concernant les Hindous dans le résultat obtenu du Surya Siddhanta pour 510 av. J.-C. Lorsque l’observation de Thalès est corrigée pour la parallaxe solaire et la réfraction à la latitude de Milet, nous avons pour l’obliquité dans le temps de Thalès 24° 00' 56 », ce qui est 15' 07 » plus grand que celui qui est calculé d’après la formule de Newcomb.
En ce qui concerne cette valeur de 24° à peu près à l’époque de Thalès en 558 av. J.-C., et des anciens Hindous en 510 av. J.-C., il est intéressant de noter l’opinion de Tannery, l’éminente autorité française en matière d’astronomie ancienne, concernant la valeur des observations grecques anciennes. Il montre que la mesure exacte de la circonférence de la terre par Ératosthène en 230 av. J.-C., n’était « nullement le résultat d’un heureux accident », et dans L’Astronomie Ancienne, p. 120, il fait les remarques suivantes concernant la mesure par Ératosthène de l’obliquité de l’écliptique :
Avant la mesure d’Eratosthène, l’obliquité était évaluée à 1/15 du cercle, soit 24°. Cette détermination, indiquée par Eudème sur le rapport de Dercyllide (Théon de Smyrne), était déjà indiscutablement connue d’Eudosse, et peut-être était-elle antérieure à lui, remontant à l’école de Pythagore. Elle est évidemment liée à la solution, donnée par Euclide, du problème de l’inscription, dans un cercle, du pentagone régulier, cette solution ayant pour objet le traçage du cercle moyen du zodiaque sur la sphère céleste. Le processus à suivre pour mesurer l’obliquité de l’écliptique était alors connu dès le début de l’astronomie grecque. Eratosthène prit le rôle de douter de l’exactitude de la simple relation universellement admise devant lui, et d’entreprendre une mesure qu’il sut rendre si exacte qu’elle fit désespérer à ses successeurs de faire mieux.
Tannery souligne également qu’Eratosthène « s’en
tint naturellement au procédé, déjà familier dans toutes les villes
grecques, d’observer les ombres du gnomon ».
En ce qui concerne la suggestion de Tannery selon laquelle la
détermination de 24° pour l’obliquité de l’écliptique remonte à
l’école de Pythagore, nous verrons que cette suggestion est
correcte.
Pythagore a commencé à voyager à la recherche de la connaissance à l’âge de 18 ans. Après avoir visité la Phénicie et la Syrie, il se rendit en Égypte, où il passa 22 ans à étudier, qui s’y terminèrent par la conquête de l’Égypte par Cambyse, roi de Perse, en 525 av. J.-C. Il fut emmené à Babylone en captivité, mais continua ses études parmi les Chaldéens et les Perses Magoi. Après cela, il visita l’Inde, la Celtique, la péninsule ibérique et la Sicile, puis s’installa à Crotone dans le sud de l’Italie.
Nous pouvons donc conclure que l’école de Pythagore, où il effectuait des observations astronomiques, fut établie vers l’an 515 av. J.-C. D’après la nouvelle courbe et la nouvelle formule, l’obliquité de l’écliptique à cette période était de 24° 00' 05". C’est pourquoi Tannery a eu raison d’attribuer la valeur 24° à une date correspondant à l’école de Pythagore.
Pythéas de Massilia (l’ancienne Marseille, qui était alors une importante colonie grecque), est célébré comme un grand navigateur et géographe, à l’époque d’Alexandre le Grand, en 325 av. J.-C. Il était aussi astronome, et fut l’un des premiers à faire des observations de latitude, entre autres, celle de sa ville natale Massilia, qu’il fixa avec une précision remarquable, de sorte que son résultat fut adopté par Ptolémée, et devint la base de sa carte de la Méditerranée occidentale.
Il fut aussi le premier parmi les Grecs à se faire une idée correcte des marées. Il indiqua leur connexion avec la lune et indiqua leurs changements périodiques en fonction des phases de la lune.
Dans son célèbre voyage d’exploration, Pythéas visita la Grande-Bretagne et en explora une grande partie, ajoutant un récit de Thulé, qui pourrait être les îles Orcades et Shetland, ou même l’Islande, puis visita toutes les côtes de l’Europe, y compris probablement la Baltique jusqu’à l’embouchure de la Vistule.
À propos de ce voyage, R.T. Gunther, dans sa description des anciens instruments d’arpentage, dit :
Vers 326 av. J.-C., en préparation d’un voyage de découverte, qui se termina par la découverte de notre île de Bretagne, Pythéas navigua de Phocée à Marseille. Là, il érigea un grand gnomon divisé en 120 parties, et fixa sa latitude avec un résultat qui semble presque incroyablement exact, car, en appliquant le demi-diamètre du soleil, qu’il a omis, la latitude qu’il a obtenue ne diffère pas de plus d’une minute de la latitude réelle de l’observatoire de Marseille. (1)
Les chiffres des observations de Pythéas au solstice d’été à Marseille sont donnés par Strabon et Ptolémée. En utilisant la latitude de l’ancien observatoire de Marseille, qui est près du port, et en appliquant des corrections pour la parallaxe solaire, le demi-diamètre et la réfraction, nous obtenons l’obliquité de l’écliptique à partir de l’observation de Pythéas en 326 av. J.-C. : 23° 53' 46". C’est 9 pi 38 po de plus que la valeur calculée à partir de la formule de Newcomb. À mesure que nous poussons la comparaison dans l’ère chrétienne, nous verrons cette différence devenir de moins en moins grande. À l’inverse, si l’on remonte à l’époque av. J.-C., l’échec de la formule à rendre compte du changement anormal de l’obliquité, révélé par les observations anciennes, est de plus en plus évident.
Il est intéressant de comparer la valeur de l’obliquité obtenue à partir des observations faites par Pythéas en 326 av. J.-C. avec les observations faites à Marseille, près de 2000 ans plus tard, c’est-à-dire par les astronomes français Nicolas Claude de Peiresc et Pierre Gassendi au solstice d’été en 1636 après J.-C. Ce qui suit est tiré d’un compte rendu donné par G. Bigourdan des opérations de Peiresc :
Tout en accordant une grande attention à la question des longitudes, dont les erreurs étaient énormes, même à nos portes, Peiresc ne négligeait pas la question des latitudes .......
Il recommandait surtout qu’ils soient déterminés par les altitudes méridiennes du soleil, particulièrement aux solstices d’été, en employant le gnomon, qui pourrait alors rivaliser avantageusement en précision avec le meilleur instrument de l’époque.
Et il en donna lui-même l’exemple avec Gassendi en répétant à Marseille, au solstice d’été de 1636, la mémorable observation de Pythéas. Déjà l’année précédente, Wendelin lui avait demandé de faire cette observation, afin d’élucider la question de la variabilité de l’obliquité de l’écliptique.
Diverses circonstances fortuites ayant retardé cette observation, elle fut faite en 1636. Le choix d’un endroit convenable présentait quelques difficultés. Finalement, il fut décidé d’utiliser l’église du collège de l’Oratoire, alors en construction, où, avec l’accord des autorités religieuses et consulaires, Peiresc fit abattre certaines sections du mur, percer le toit et déplacer une planche. Voici ce qu’il écrivit à d’Arcos le 20 juillet 1636 :
« Nous fîmes préparer un matin une machine de 18 cannes (a) de diamètre, dont le gnomon avait plus de 9 cannes de hauteur, et elle fut divisée en plus de 80 000 parties reconnaissables, de sorte que l’on pouvait reconnaître et déterminer la différence de celle sur laquelle l’ombre solaire tombait précisément, exclusivement des autres parties, soit au-dessus, soit au-dessous. Tout cela fut fait avec tant d’habileté et avec si peu de frais que tous ceux qui étaient présents furent ravis. (b) Nous n’avions qu’à percer le toit d’un bâtiment très élevé, de trois ou quatre étages, et recevoir le rayon du soleil en bas, après avoir bien ajusté avec le fil à plomb perpendiculairement à la ligne méridienne, qui était tracée en bas, et avoir enlevé quelques briques à une hauteur de 9 cannes pour mesurer plus exactement la distance entre le trou dans le toit et la base du de la ligne méridienne. ..........
La hauteur du gnomon était de 51 pieds 8 pouces 4 lignes (c) 0 parties, ou 89 328 parties (douzièmes de ligne), et l’ombre a été trouvée à 31 750 parties.
|
En utilisant la latitude de l’ancien observatoire de Marseille, près du port, l’obliquité calculée à partir de l’observation de Peiresc est de 23° 30' 23". C’est remarquablement exact, n’étant différent que de 1' 11 » de la valeur dérivée de la formule de Newcomb, et encore moins, de 35 » de la nouvelle courbe.
En plus de démontrer la précision que l’on peut obtenir avec le gnomon, l’observation de Peiresc montre que la différence entre son résultat et celui de Pythéas en 326 av. J.-C. confirme notre croyance que, dans les âges passés, il y a eu un changement marqué dans l’obliquité de l’écliptique, au-delà du changement normal correspondant à la formule de Newcomb.
C’est
ce que montre la comparaison suivante :
- Valeurs observées de l’obliquité
- Valeurs calculées de l’obliquité par Newcomb
Pythéas, 326 av. J.-C. (2) 23° 53' 46"
Peiresc, 1636 apr. J.-C. 23° 30' 23"
Différence 23' 23"
326 av. J.-C. 23° 44' 08"
1636 23° 29' 12"
Différence 14' 56"
Excédent de 1 sur 2 = 8' 27"
Nous allons maintenant voir comment cette conclusion est conforme
aux résultats obtenus par trois autres astronomes grecs célèbres des
temps anciens, Ératosthène, Hipparque et Ptolémée.
Eratosthène est né à Cyrène, chef-lieu de l’ancienne colonie grecque de Cyrénaïque, en Libye, en Afrique du Nord, en 276 av. J.-C. Après des études à Alexandrie et à Athènes, il est nommé, à l’âge de 41 ans, par Ptolémée Euergète, surintendant de la célèbre bibliothèque, musée et observatoire d’Alexandrie. Il y resta jusqu’à sa mort, à l’âge de 82 ans, en 194 av. J.-C.
Ératosthène a été appelé le cosmographe, ou arpenteur, de l’univers, à cause de sa célèbre mesure de la circonférence de la terre vers 230 av. J.-C. Il a accepté la doctrine pythagoricienne selon laquelle la terre est une sphère, tournant sur son axe. Il en conclut qu’il serait possible de mesurer la circonférence de la terre par une méthode simple en principe, mais nécessitant un travail d’une ampleur considérable, pour la mettre en œuvre.
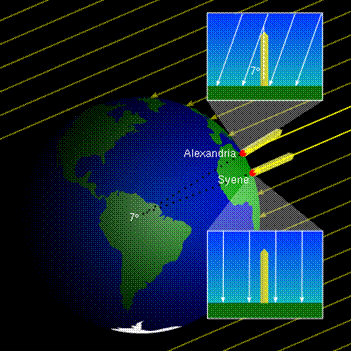
Cette méthode consistait à mesurer, par des observations astronomiques, l’arc dans le ciel entre la position solstitielle d’été du soleil lorsqu’il était au-dessus de Syène [l’Assouan ou Assouan moderne, près du site du grand barrage d’Assouan (Assouan)], et sa position en même temps à Alexandrie. La contrepartie terrestre de cela était la distance entre Syène et Alexandrie, à mesurer à la surface de la terre, puis à réduire par calcul à la distance vraie entre les parallèles de latitude passant par Syène et Alexandrie. La circonférence de la terre pourrait alors être déterminée par la simple proportion de ces arcs célestes et terrestres par rapport au cercle complet de 360°.
L’attention du lecteur est particulièrement attirée sur cet ouvrage d’Ératosthène, car il est certain qu’il a pris grand soin de ces observations historiques. Ils nous donnent un test crucial de la divergence entre les anciennes observations de l’obliquité de l’écliptique et la théorie moderne.
La première mesure de la circonférence de la terre, il y a 2180 ans, a été effectuée de manière efficace et excellente. Outre les observations astronomiques de Syène et d’Alexandrie, une mesure complète de la distance terrestre entre ces deux lieux a été faite. Des arpenteurs égyptiens, appelés Bematistoi (meneurs professionnels) étaient employés à cette fin. Ils ont mesuré la grande distance de 640 milles le long de la piste sinueuse, suivant le cours du Nil, de Syène à Alexandrie. Strabon nous apprend que les allocations ont été coupées pour les routes irrégulières (3), et donne la distance trouvée par Eratosthène, de la petite cataracte du Nil, près de Syène, à la mer, comme 5300 stades (518 milles). La première cataracte se trouve à 2 milles au sud de Syène, et l’ancienne bibliothèque et l’observatoire d’Alexandrie étaient à environ un kilomètre de la mer.
La route d’Alexandrie à Syène ne va pas plein sud, mais est d’abord sud-est sur 125 miles (d’Alexandrie au Caire) ; et à partir du Caire, il y a une tendance dominante du SSE au SE sur une grande partie du chemin, qui comprend le Grand Coude de 80 milles entre Hammadt et Erment, où il y a une grande déviation de la ligne méridienne.
Ératosthène a donc réduit la distance de 5300 stades (518 3/4 miles) à 5000 stades (489,33 miles) pour donner la distance méridionale, c’est-à-dire la distance corrigée entre les parallèles de latitude passant par Syène et Alexandrie. Le stade utilisé par Eratosthène mesurait 516,73 pieds de long. La distance réelle entre ces parallèles, d’après les calculs modernes, est de 489 milles, presque exactement la même que celle qui a été estimée par Ératosthène.
En ce qui concerne l’arc céleste entre la position aérienne du soleil aux solstices d’été de Syène et d’Alexandrie, Cléomède le donne en chiffres ronds comme un cinquantième du cercle de 360°, c’est-à-dire 7°.2 . En combinant cela avec l’arc terrestre de 5000 stades, la circonférence approximative de la terre a été donnée en chiffres ronds comme étant de 250 000 stades, soit 24 466 milles. Le résultat final donné par Ératosthène était de 252 000 stades, ce qui équivaut à 24 661 milles. Les mesures modernes donnent la circonférence polaire de la Terre à 24 860 milles et la circonférence équatoriale à 24 902 milles. La mesure de la circonférence polaire par Eratosthène n’était donc que de 199 miles inférieure à la valeur moderne.
Passons maintenant aux mesures astronomiques. La valeur précise de l’obliquité de l’écliptique enregistrée par Ératosthène est impliquée dans cette mesure historique du monde. Cependant, elle ne repose pas uniquement sur cette opération, mais est le résultat de l’observation des ombres solsitaires sur une période de plusieurs années, tant à Alexandrie qu’à Syène, ainsi qu’en d’autres lieux. C’est ce qui ressort des informations qui nous sont parvenues par Strabon, Cléomède et Pline ; bien que, malheureusement, le livre spécial d’Ératosthène décrivant la mesure de la terre, et désigné par Macrobe comme « Libri dimensionum », ait été perdu.
à partir de http://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Eratosthenes.bjb.svg/400px-Eratosthenes.bjb.svg.png
À Syène se trouvait le célèbre « puits d’Eratosthène », où, de son temps, on voyait le soleil à midi le jour du solstice d’été « éclairer le puits jusqu’à l’eau, et ne pas projeter d’ombre sur les côtés ».
Le puits d’Eratosthène à Syène

Vue vers le bas dans le puits

à partir de http://www.mlahanas.de/Greeks/images/eratosthenes2.jpg
Avant le solstice, le côté nord du puits était entièrement éclairé à midi, mais le côté sud était dans l’ombre. À l’approche du solstice, l’ombre se retira vers le bord le plus bas du côté sud, jusqu’à ce que le jour du solstice, aucune ombre ne puisse être perçue de ce côté. Le bord nord du soleil était alors exactement et verticalement au-dessus du puits. Ce fait est également établi par des déclarations confirmatives concernant les ombres du gnomon à Syène.
Selon une déclaration attribuée à Eratosthène, « à Syène, le gnomon
ne jetait aucune ombre le jour du solstice d’été ». C’est ce que
confirme Strabon, qui dit (Géographie, livre
11, chap. 5) : « Car le tropique d’été passait par Sienne, parce
qu’au moment du solstice d’été, le gnomon ne projetait pas d’ombre à
midi. » Plutarque mentionne également « les gnomons de Syène, qui
apparaissent libres de toute ombre au solstice d’été ». (5)
Il faut bien se rappeler que ces ombres, qu’elles soient au Puits ou
projetées par le gnomon, ne correspondent pas au centre du soleil,
mais à son bord septentrional. Pour réduire donc les observations au
centre du soleil, à des fins de comparaison avec les observations
modernes, nous devons appliquer les corrections nécessaires non
seulement pour la parallaxe et la réfraction, omises par les anciens
observateurs, mais aussi pour la beaucoup plus grande du bord du
soleil à son centre. Cela fait, nous constatons que les observations
faites par Eratosthène étaient remarquablement précises. Ainsi, dans
le cas d’Alexandrie, la latitude utilisée par Ératosthène était de
30° 58' N., déterminée à partir de ses observations du bord nord du
soleil. Les corrections totales, comme ci-dessus, s’élevant à 13'
52 », doivent être ajoutées à la latitude d’Alexandrie
d’Ératosthène, 30° 58', ce qui donne la latitude du musée
d’Alexandrie 31° 11' 52 » N. Ce site antique se trouve à l’angle de
l’actuelle rue Sesostris et de la rue de l’église copte ; et le
Survey General d’Égypte donne sa latitude réelle à 31° 11' 50 » N.,
soit seulement 2 » de moins que la valeur trouvée d’après les
observations d’Ératosthène. Nous voyons donc que les observations
faites par Eratosthène apparaissent sous un jour très favorable
quant à leur exactitude.
En
ce qui concerne la latitude de Syène, le célèbre puits
d’Erastosthène à cet endroit se trouve à la latitude 24° 05' 06" N.,
selon les mesures modernes fournies par l’arpenteur général de
l’Égypte. Or, Eratosthène prit pour latitude de cet endroit 23° 51'
15", déterminé comme auparavant, à partir du bord nord du soleil.
C’était aussi la même chose que l’obliquité de l’écliptique, qu’il
obtenait de ses observations avec le gnomon à Syène, lorsque le bord
nord du soleil était verticalement au-dessus de sa tête au moment du
solstice d’été, et que le gnomon ne projetait donc aucune ombre à
midi.
Quand, comme cette fois, le soleil est au zénith, il n’y a ni
parallaxe ni réfraction, et la seule correction nécessaire pour
obtenir la vraie latitude est la correction du bord du soleil à son
centre, c’est-à-dire 13' 13". Si l’on ajoute cela à l’altitude
d’Eratosthène à Syène, 23° 51' 15 », nous obtenons 24° 04' 28 » N.
Ce résultat n’est inférieur que de 38 » à la latitude réelle de 24°
05' 06 » N., et constitue une confirmation remarquable, non
seulement de l’exactitude des observations d’Ératosthène à Syène,
mais aussi de l’obliquité de l’écliptique 23° 51' 15 » à la date de
ses observations, c’est-à-dire en 230 av. J.-C.
La relation entre la latitude de Syène et l’obliquité de
l’écliptique sera peut-être rendue plus claire par l’examen du
schéma suivant.
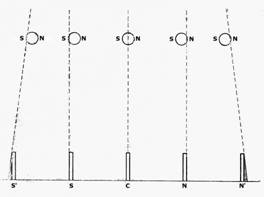
DIAGRAMME
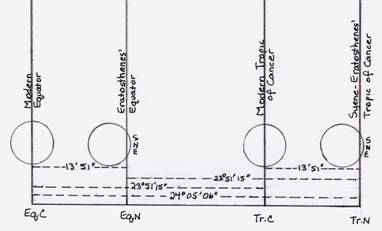
SNE est « le bord nord du soleil ».
(1) L’équation C représente un endroit sur l’équateur terrestre où
le centre du soleil est verticalement au-dessus de la tête à midi le
jour de l’équinoxe. C’est l’équateur selon la définition moderne.
(2) L’Éq.N représente un endroit à environ 14 milles au nord de
l’Éq.C., où le bord nord du soleil est verticalement au-dessus de la
tête à midi le jour de l’équinoxe. À cette époque, un gnomon se
trouvait n’importe où au nord de l’Eq.N. projette une ombre sur son
côté nord, mais à l’Éq.N, elle ne projette aucune ombre. L’Éq.N
était donc l’équateur tel qu’Ératosthène le définissait.
(3) Tr.C représente une position sur le tropique du Cancer, où le le
centre du soleil était verticalement au-dessus de la tête à midi le
jour de la Solstice.
(4) Tr.N représente la position de Syene, à environ 14 miles au nord
de Tr.C, où le bord nord du soleil était
au-dessus de la tête à midi le Le jour du solstice d’été.
C’était le « tropique du cancer » d’Eratosthène, où le soleil ne
projetait alors aucune ombre sur le puits d’Eratosthène, et où les
gnomons étaient également libres d’ombre.
D’après ce diagramme, le lecteur verra que l’obliquité de
l’écliptique, telle qu’elle est définie dans le système moderne,
Eq.C - Tr.C, (c’est-à-dire la distance maximale du soleil à
l’équateur), est exactement égale à l’obliquité dans le système
adopté par Ératosthène, c’est-à-dire Eq.N - Tr.N., et qu’il a trouvé
être de 23° 51' 15". On verra aussi qu’il est prouvé que c’est la
vraie valeur, car, en appliquant la correction TrC - TrN (centre du
soleil à son bord), 13' 51 », selon la détermination d’Ératosthène,
nous obtenons la latitude vraie de Syène, c’est-à-dire 24° 05' 06 ».
Un autre point qui ressort de cette analyse est qu’Eratosthène a trouvé d’après ses observations à Alexandrie et à Syène que la latitude du premier lieu, selon son système de mesure, se rapportait à l’observation du bord nord du soleil. D’après cette mesure, la latitude d’Alexandrie était de 30° 58' N. et celle de Syène était de 23° 51' N. (à la minute d’arc la plus proche).
La différence de latitude était donc de 7° 07', ce que Cléomède donne en « chiffres ronds » comme 1/50 de l’ensemble du cercle de 360°. La fraction est plus exactement de 1/50,5. Si l’on combine cette dernière fraction, qu’Eratosthène employa finalement, avec 500 stades pour la distance à la surface de la terre entre les deux parallèles de latitude, on obtient pour toute la circonférence de la terre 252 500 stades, pour lesquels Eratosthène dans son résultat final a donné 252 000 stades, évidemment aux 1000 stades les plus proches. Cela équivalait, comme nous l’avons déjà fait remarquer, à 24 661 milles, à moins de 199 milles de la meilleure valeur moderne.
Tannery, l’éminent écrivain français sur l’astronomie ancienne, qui étudie à fond l’œuvre d’Ératosthène, dit :
« Est-il alors nécessaire de conclure que l’exactitude du résultat obtenu par Ératosthène est due à un heureux hasard ? Je ne le pense nullement, et je crois qu’il est nécessaire de faire une distinction radicale entre les méthodes que le savant Cyrénéen pouvait employer pour contrôler ses observations, et le mode d’exposition qu’il a adopté en publiant sa mesure de la circonférence de la terre.
Une attention particulière a été accordée à cette mesure de la circonférence de la terre par Ératosthène afin de souligner l’exactitude de son travail et de sa détermination de l’obliquité de l’écliptique. Celle-ci repose sur trois séries différentes d’observations, qui s’accordent dans de très petites limites :
-
Observations à Alexandrie
Ceux-ci étaient fabriqués avec le gnomon ainsi qu’avec des instruments circulaires.
Ptolémée nous apprend que l’angle de double obliquité observé par Ératosthène et Hipparque était inférieur à 47° 45' (valeur maximale) et supérieur à 47° 40' (valeur minimale).
La moyenne de ces deux est de 47° 42' 30 », et la moitié de cela nous donne
23° 51' 15 » pour l’obliquité trouvée par Eratosthène. (6) Cela n’inclut pas les corrections de parallaxe et de réfraction, ni la différence entre les demi-diamètres apparents du soleil en été et en hiver. Lorsque ces corrections sont appliquées, la valeur finale de l’obliquité de l’écliptique d’après les observations d’Ératosthène à Alexandrie est de 23° 52' 04".
-
Observations à Syène
Observations avec le gnomon
Au solstice d’été, on remarqua que le gnomon de Syène ne projetait pas d’ombre à midi. Le bord nord du soleil était exactement au zénith. Il n’y avait donc pas de parallaxe ou de réfraction, et la seule correction est la réduction du bord de l’ombre du soleil vers son centre. En utilisant la latitude vraie, qui est connue, et en appliquant cette correction, nous obtenons pour l’obliquité au solstice d’été 23° 51' 53.
Au solstice d’hiver : il est dit par Cléomède que les observations de l’ombre du gnomon faites par Eratosthène au solstice d’hiver à Syène et à Alexandrie ont donné le même résultat pour la différence de latitude entre les deux lieux qu’au solstice d’été. Nous prenons donc pour Syène le même double angle d’obliquité que celui trouvé à Alexandrie. En appliquant les corrections nécessaires comme précédemment, nous trouvons pour l’obliquité à Syène pour les deux solstices, 23° 54' 02".
Observations au puits d’Eratosthène
Selon la description donnée par Howard Payn (Observatory, 1914, p.287), le puits a maintenant environ 25 pieds de profondeur et a des marches en spirale menant à l’eau. Cela peut faire partie d’une reconstruction ultérieure. Strabon s’y réfère (XVII, ch. 1. p. 48) comme suit :
Mais à Syène se trouve aussi le Puits qui marque le tropique d’été, pour la raison que cette région se trouve sous le cercle tropique et fait que le gnomon ne projette aucune ombre à midi ; car si de notre région, je veux dire celle de la Grèce, nous nous dirigeons vers le sud, c’est à Syène que le soleil passe d’abord au-dessus de nos têtes et fait que le gnomon ne projette aucune ombre à midi ; et nécessairement lorsque le soleil passe au-dessus de nos têtes, il jette aussi ses rayons dans des puits jusqu’à l’eau, même s’ils sont très profonds ; car nous sommes nous-mêmes perpendiculaires à la terre, et les puits sont creusés perpendiculairement à la surface. Et ici sont stationnés trois cohortes (7) en tant que garde.
L’affirmation selon laquelle Syène est le premier endroit où cela se produit est importante, et le puits donne une preuve confirmative de l’obliquité trouvée pour l’observation du solstitiel d’été avec le gnomon de 23° 51' 53".
Observations dans la zone sans ombre
Posidonius savait, d’après l’autorité d’Ératosthène, qu’à Syène, sous le tropique du Cancer, au moment où le soleil est dans la constellation du Cancer, on ne voit pas d’ombres à midi dans une zone de 300 stades de diamètre.(8)
Strabon y fait référence dans son Livre de Géographie II, Chapitre 5, paragraphes 36, 37 :
À Syène, à Bérénice sur le golfe Persique, et dans le pays des Troglodytes, le soleil se trouve au zénith au moment du solstice d’été.... dans toutes les régions qui se trouvent entre le tropique et l’équateur, les ombres tombent dans les deux sens, c’est-à-dire vers le nord et vers le sud, mais dans celles de Syène et loin des tropiques d’été, les ombres à midi tombent vers le nord ; et les habitants des premières régions sont appelés Amphisques (les deux ombres), et de la seconde Hétérosques (autres ombres), tous dont les ombres tombent toujours vers le nord comme c’est le cas chez nous, ou toujours vers le sud comme c’est le cas pour les habitants de l’autre zone tempérée.
(Strabon parle ici des gens en Afrique vivant dans la zone tempérée au sud du tropique du Capricorne, où les ombres solaires à midi tombent toujours vers le sud).
D’après les déclarations de Strabon, Syène, par 24° 05' 06 » de latitude nord, se trouvait exactement sur la limite nord de la zone sans ombre, qui s’étendait vers le sud sur 300 stades, ce qui équivaut à 29,36 milles ou 25' 36 » de latitude, c’est-à-dire à 23° 39' 30 » de latitude.
Le centre exact de la zone sans ombre, c’est-à-dire là où le centre du soleil était verticalement au-dessus de la tête à midi le jour du solstice d’été, était donc, à l’époque d’Ératosthène, à mi-chemin entre les latitudes 24° 05' 06 » et 23° 39' 30 », c’est-à-dire à la latitude 23° 52' 18 ». C’était donc la distance maximale du centre du soleil par rapport à l’équateur céleste au moment du solstice d’été ; c’est-à-dire que l’obliquité de cette observation était de 23° 52' 18".
|
La zone sans ombre : tropique du Cancer
SN = 300 stades = 29,36 milles = 25' 36" de latitude
|
En résumé, nous avons pour l’obliquité de l’écliptique, dérivée des observations d’Ératosthène :
| Observations faites à Alexandrie |
23° 52' 04" aux deux solstices
|
| Observations à Syène |
23° 52' 04" aux deux solstices
|
| Observations à Syène au solstice d’été avec le gnomon, et à Puits d’Eratosthène |
23° 51’ 53”
|
| Observations à Zone sans ombre |
23° 52' 18"
|
|
Méchant
|
23°
52’ 05”
|
Nous voyons à quel point ces résultats sont concordants, et l’analyse donnée ci-dessus indique une grande mesure de fiabilité. Lorsque nous comparons le résultat moyen, 23° 52' 05", avec le résultat obtenu par calcul pour la même date, 230 av. J.-C., d’après la formule de Newcomb, nous trouvons une grande différence.
Obliquité
Eratosthène 230 av. J.-C. 23° 52' 05 »
Newcomb 230 av. J.-C. 23° 43' 47 »
Différence 8' 18"
Cela confirme de manière frappante la différence entre la formule de Newcomb et les observations faites par Pythéas (9' 38 » en 326 av. J.-C.), Thalès (15' 07 » en 558 av. J.-C.) et les anciens Hindous (15' 16 » vers 510 av. J.-C.).
En comparant également avec les résultats chinois et hindous antérieurs, nous voyons comment la différence augmente à rebours jusqu’aux temps les plus anciens.
Il est clair que ces anciennes observations révèlent inévitablement le fait qu’il y a eu un mouvement de la terre dans le passé qui n’est pas expliqué par la théorie moderne représentée dans la formule de Newcomb.
Hipparque est né vers 190 av. J.-C., soit à Rhodes, soit à Nicasa, une ville importante - ou métropole - de Bithynie, en Asie Mineure. Il mourut vers 120 av. J.-C. Hipparque effectua la plupart de ses travaux astronomiques à Rhodes, la capitale de l’île de Rhodes, dans la mer Égée, célèbre pour son beau climat ; où l’on dit qu’il n’y a guère de jour dans l’année où le soleil n’est pas visible.
Rhodes était également célèbre comme le site du Colosse de Rhodes, l’une des sept merveilles du monde antique. Il s’agissait d’une statue de bronze colossale du dieu solaire grec Hélios, de 70 coudées (106 pieds de haut) à l’entrée du port. Il a été réalisé par le sculpteur Charès, mais a été détruit par un tremblement de terre en 224 av. J.-C., 56 ans après son érection.
Hipparque construisit un observatoire à Rhodes, où il fit ses principales observations et calculs. Il visita également Alexandrie et y utilisa les instruments astronomiques du musée d’Alexandrie. Hipparque est généralement reconnu comme le plus grand astronome du monde antique et se classe parmi les plus grands astronomes de tous les temps. Il était très admiré par Ptolémée, qui le louait comme « un homme aimant le travail et la vérité ».
Hipparque fut le premier homme à compter les étoiles, ce qui était considéré dans les premiers temps comme une entreprise prodigieuse, voire présomptueuse, « rem etiam Deo improbam » (Pline). Il inventa la méthode de description des positions des étoiles par les longitudes et les latitudes célestes, système adopté par la suite par les géographes pour cartographier la Terre. Son catalogue original de 1080 étoiles, donnant leurs positions et leurs magnitudes, classées selon leurs constellations, pour l’année 129 av. J.-C., est malheureusement perdu. Mais une copie, comprenant 1028 étoiles, révisée à la date de 137 après J.-C., nous est parvenue dans les livres 7 et 8 de l’Almageste de Ptolémée.
Hipparque est donc considéré comme le fondateur de l’astronomie d’observation. Il fit la grande découverte de la précession des équinoxes, et inventa la trigonométrie, à la fois plane et sphérique. Il calcula des tables solaires et lunaires pour prédire les positions du soleil et de la lune, ainsi que leurs éclipses, et redétermina les durées de l’année et du mois. Ses observations étaient très étendues et il inventa de nouveaux instruments pour augmenter leur précision.
En particulier, en ce qui concerne le sujet de cette étude, il a vérifié l’obliquité de l’écliptique obtenue par Ératosthène en 230 av. J.-C., 65 ans avant son époque, et a trouvé exactement le même résultat. À ce sujet, Wendelin dit que Hipparque
d’après ses propres observations, il a déclaré que la distance entre les tropiques était proportionnelle à l’ensemble du cercle comme 11 l’est à 83, exactement la même que celle d’Ératosthène, et a trouvé l’obliquité maximale de 23° 51' 20".Il a également utilisé cette valeur, comme en témoigne Ptolémée. Ptolémée est également d’accord sur l’année où cette observation a été faite, car en l’an 43 de la troisième période callipique, il a commencé à écrire avec la plus grande vigueur, après être revenu sept ans plus tôt d’Alexandrie dans sa ville natale de Rhodes, où il a pris une vie paisible. Je ne pense pas que cette valeur de l’obliquité doive être rapportée à une autre année ; Cette année était 135 avant notre ère.
Hipparque, comme les autres astronomes de l’Antiquité, n’appliquait aucune correction pour la parallaxe, la réfraction ou le demi-diamètre du soleil, et ses observations à Rhodes ont été faites avec le gnomon vertical. En appliquant ces corrections nécessaires, nous obtenons pour l’obliquité de l’écliptique, résultant des observations d’Hipparque à Rhodes 23° 52' 16". La valeur calculée par la formule de Newcomb pour la même date est de 23° 42' 43".
Ici encore, nous voyons une différence frappante, à savoir 9' 33", entre l’observation ancienne faite par Hipparque et la valeur calculée. Hipparque était beaucoup trop bon observateur pour avoir commis une erreur aussi grande que 9,5 minutes dans ses observations, et nous pouvons comparer cela avec le commentaire de Kepler sur les observations de Tycho Brahe au XVIe siècle. Après tous les efforts imaginables pour faire concorder la théorie astronomique de son époque avec les observations de Tycho sur les planètes, Kepler a encore trouvé des erreurs s’élevant à huit minutes de degré. Il déclara alors sans hésitation qu’il croyait en l’exactitude des observations de Tycho, et affirma qu’il était si bon observateur qu’il était impossible que ses observations soient erronées jusqu’à l’expiration de 8 minutes. Il a ajouté : « À partir de ces huit minutes, nous construirons une nouvelle théorie qui expliquera les mouvements de toutes les planètes. » Il l’a fait en abandonnant l’idée platonicienne selon laquelle les planètes se déplaçaient en cercles parfaits, et en substituant des orbites elliptiques à toutes les planètes, ayant le soleil au centre de l’orbite elliptique de chaque planète.
De la même manière, nous pouvons affirmer, avec l’appui de toutes les observations anciennes examinées jusqu’à présent, que les 9,5 minutes d’Hipparque ont conduit à une nouvelle théorie, qui, combinée à la théorie existante, explique le mouvement complet de la terre dans la variation de son inclinaison axiale au cours des 4000 dernières années.
Le célèbre astronome Claudius Ptolémée est né vers 70 après J.-C. en Égypte, à Péluse, une ancienne ville située à l’embouchure la plus orientale du Nil ; il est mort vers 147 après J.-C. Ptolémée est célébré comme le fondateur du système ptolémaïque de l’univers, qui a régné pendant plus de 1500 ans, lorsqu’il a finalement été remplacé par le système copernicien.
Ptolémée était un grand mathématicien, géographe et astronome, et était considéré par les anciens comme le « prince des astronomes ». Sa Megale Syntaxis, appelée plus tard l’Almageste de Ptolémée, en 13 livres, a conservé et nous a transmis les observations et les découvertes des anciens astronomes, et forme un compte rendu des plus remarquables et des plus complets de l’astronomie de son temps. C’était le manuel standard d’astronomie pendant 1500 ans.
Ptolémée donne l’obliquité de l’écliptique pour son temps comme 23° 51' 20". Ceci est évidemment tiré des observations d’Hipparque. Il est probable que Ptolémée n’a pas fait lui-même les observations de l’obliquité de l’écliptique, mais qu’il a simplement pris cette valeur d’Hipparque, à cause de sa haute opinion de l’exactitude des observations faites par ce grand astronome, et de leur accord avec l’obliquité trouvée par Ératosthène.
Néanmoins, nous sommes en mesure d’obtenir une valeur indépendante à partir des nombreuses observations de Ptolémée de la lune à l’époque où elle était à sa moindre distance du zénith d’Alexandrie. L’astronome belge médiéval Wendelin l’a souligné dans ses mémoires L’obliquité du soleil (Solis Obliquitas). Dans cet ouvrage, il souligne, à propos des observations de Ptolémée, que
Ptolémée lui-même rapporte de nombreuses observations de la lune en quadrature, (c’est-à-dire au premier quart de phase de la lune lorsqu’elle est exactement à 90 degrés à l’est du soleil), distante du zénith d’Alexandrie de 2 1/8 degrés, c’est-à-dire 2° 7' 30".
Lorsque cette distance observée est corrigée pour la réfraction et la parallaxe lunaire, elle est réduite à 2° 5' 26". Or, cette observation, comme l’explique Wendelin, se rapporte à la distance zénithale de la lune à une période de son cycle de 19 ans où, au solstice d’été du soleil, la lune au même moment était à sa distance maximale - 5° 18' 0" au nord de l’écliptique. Cela s’est passé à l’époque de Ptolémée, en l’an 126 après J.-C.
Il ne nous reste plus qu’à additionner les deux grandeurs 2° 5' 26 » et 5° 18' 0 », ce qui donne 7° 23' 26 », qui était la distance réelle de l’écliptique, à son point de croisement avec l’équateur céleste, du zénith d’Alexandrie. Nous soustrayons maintenant cette quantité de la latitude du musée d’Alexandrie, et nous obtenons ainsi l’obliquité de l’écliptique 23° 48' 24" en l’an 126 après J.-C., d’après les observations de Ptolémée lui-même sur la lune.
Il est très intéressant de noter que ces observations ont été faites avec un instrument spécial inventé par Ptolémée pour ses observations lunaires, appelé « Organon Parallaktikon » ou « Regula Ptolemaica », plus tard appelé Règles de Ptolémée ou Triquetrum. La visée a été suffisamment grande pour couvrir tout le disque de la lune, et une petite mire arrière a été utilisée. Il était capable de donner des résultats précis, et 1400 ans plus tard, Copernic, à l’aide d’un instrument du même type, « a fait les mesures avec lesquelles il a renversé le système ptolémaïque et nous a donné une nouvelle idée de l’univers ».
Lorsque nous comparons l’obliquité ainsi obtenue d’après les observations de Ptolémée, 23° 48' 24 », avec celle qui est calculée par la formule de Newcomb, à savoir 23° 40' 47 », nous trouvons une différence de 7' 37 ». C’est encore une confirmation des résultats précédents, montrant également la diminution progressive de la différence à mesure que nous avançons vers l’ère moderne.
Tant de résultats tendant tous dans la même direction, provenant de pays, d’âges et d’observateurs différents, suffisent à l’étudiant de cet ouvrage pour voir que la théorie astronomique moderne ne révèle pas toute l’histoire du changement de l’inclinaison de l’axe de la terre au cours des âges passés. Nous voyons, au contraire, que ces anciennes observations indiquent un changement d’une grande et profonde importance dans l’histoire de la terre.
********************
-
R.T. Gunther, Les premières sciences à Oxford, 1923, vol. 1. p. 330 « Instruments d’arpentage anciens » retour au texte
-
Voir aussi le tableau 25 [qui sera ajouté ultérieurement] retour au texte
-
Strabo. Géographie, Vol. 1. Livre 11, ch. 4, par. 4 retour au texte
-
J.L.E. dreyer, « Planetary Systems », p. 175 retour au texte
-
Plutarque. Opera Moralia sur la cessation des oracles 1V retour au texte
-
Ptolémée. Syntaxis II. Chapitre 12 retour au texte
-
Une cohorte était un dixième d’une légion et comprenait entre 500 et 600 hommes.
-
J.L.E. Dreyer. Systèmes planétaires p.185. 300 stades équivalent à 29 1/2 milles Retour au texte