CHAPITRE SIX
OBSERVATIONS DE L’OBLIQUITÉ DE L’ÉCLIPTIQUE FAITES PAR LES ARABES ET LES PERSES MÉDIÉVAUX
De nombreuses observations de l’obliquité de l’écliptique ont été faites par les astronomes arabes et perses entre les années 830 et 1020 après J.-C.
Les sites des observations étaient les suivants :
| Site | Latitude | Longitude |
|
Bagdad (Irak)
|
33° 21' N. | 44° 28' E. |
|
Rakka (près de l’Euphrate en Syrie
|
35° 57' N. | 39° 55' E. |
|
Damas (Syrie)
|
33° 30' N. | 36° 18' E. |
|
Shiraz (Perse)
|
29° 30' N | 52° 40' E. |
|
Edessa (Turquie en Asie)
|
37° 11' N. | 38° 55' E. |
|
Le Caire (Égypte)
|
30° 03' N. | 31° 15' E. |
Le premier observatoire arabe à Bagdad, combiné à une magnifique bibliothèque, et appelé la « Maison de la Sagesse », a été érigé vers 820 après JC par le septième calife de Bagdad, Al Mamun, fils de Haroun al Raschid. En plus de sa célèbre mesure d’un degré de latitude à la surface de la Terre, pour déterminer la taille de la Terre, Al Mamun s’est également donné beaucoup de mal pour déterminer l’obliquité de l’écliptique.
Certaines autorités donnent ses résultats à 23° 33', mais les Arabes ont généralement adopté 23° 35' comme la valeur la plus fiable. Ibn Junis rapporte le passage suivant d’Ebn-Hatem-Alnairizi (quelque temps après la mort d’al Mamun en 833 après J.-C.) :
L’Obliquité de l’Écliptique des astronomes d’Al Mamun est celle qui existe encore à notre époque. Ils l’ont observé avec une grande exactitude, et bien qu’ils n’aient pas également réussi dans leurs observations à cause des connaissances qui leur manquaient, néanmoins ces observations ont été très bien faites à cause de la taille et de l’excellence des instruments, et du peu de difficulté de l’opération, et de l’aide qu’ils ont eue. Cette obliquité est de 23° 35'.
Al Fargani (Alfraganus) vers 850 apr. J.-C., dans son manuel Éléments d’astronomie et de chronologie, qui était très apprécié dans l’Europe médiévale, donne également la valeur 23° 35' pour l’obliquité déterminée par Al Mamun. L’obliquité, dit-il, a été trouvée par Ptolémée à 23° 51', « mais selon la mesure ordonnée à être faite par Al Mamun de Pieuse Mémoire, qui a été effectuée par un certain nombre d’experts, elle est de 23° 35'. » Cette valeur est adoptée et citée tout au long du livre d’Aflraganus. (1)
Dans le développement de l’astronomie arabe, nous pouvons noter que la première étape a été la collecte de la littérature astronomique de toutes les sources disponibles : grecque, hindoue, égyptienne, persane, etc., et leur traduction en arabe.
Après le sac de Bagdad en 1258 après J.-C., la grande bibliothèque astronomique de Bagdad aurait formé le noyau de la bibliothèque mongole de Maragha en Perse, qui aurait contenu 400 000 livres. (Dr. Martin Johnson, « The Manuscripts of Bagdad Astronomers, » dans la revue « Observatory », vol. LIX, n° 746, juillet 1936, p. 216).
L’étape suivante fut la construction d’instruments nouveaux et perfectionnés pour les observations astronomiques, et la vérification, par leurs moyens, des résultats des temps anciens. Les astronomes arabes sont devenus réputés comme de bons observateurs et habiles dans la fabrication d’instruments. Ils ont également apporté d’importantes améliorations en mathématiques, introduit la notation décimale et construit des tables pour faciliter les calculs astronomiques.
Dans le califat de Mamoun, l’inclinaison de l’écliptique était obtenue à partir d’un pilier, ou gnomon, entouré de cercles concentriques, la verticale et l’horizontale étant sécurisées par un fil à plomb et un niveau d’eau. Le contact de l’ombre de la colonne avec l’un des cercles en deux points, avant et après midi, donnait un angle dont la bissection déterminait le méridien. Les distances zénithales du Soleil ont été obtenues à partir des rayons des cercles et de la hauteur du Pilier, dans un cas rapportée à 180 pieds. Pour obtenir l’inclinaison de l’écliptique et la latitude géographique, les distances maximale et minimale des méridiens solaires ont été calculées en traçant autour de l’heure des solstices.
(Dr. Martin Johnson, « Manuscrits des astronomes de Bagdad » dans la revue « Observatory » Vol. LIX, n° 746, juillet 1936, p. 223)
En général, seule la valeur finale de l’obliquité déterminée par les astronomes arabes est donnée, et les détails font souvent défaut.
Le détail des observations est cependant donné pour Al Battani et Ibn Junis. Al Battani (Albategnius), 880 après J.-C., était un astronome célèbre de Syrie. Il a fait des observations astronomiques à son observatoire d’Aracta (l’actuelle Rakka), près de l’Euphrate en Syrie, par 35° 57' de latitude nord et 39° 55' de longitude est. Ibn Junis, 1000 apr. J.-C., astronome arabe réputé et auteur des Tables hakémites, a travaillé à l’observatoire bien équipé du Caire. Toutefois, avant de décrire leurs observations, il est souhaitable de se référer aux corrections qui doivent être appliquées aux observations arabes en général.
Corrections apportées aux observations arabes
(1) La réfraction : Les Arabes n’appliquaient aucune correction pour la réfraction, de sorte que toutes leurs observations nécessitent cette correction.
(2) Demi-diamètre du Soleil : À l’époque d’Al Khujandi (994 apr. J.-C.) et d’Ibn Junis (1000 apr. J.-C.), une forme de gnomon se terminant par une plaque au sommet avec un trou central, pour donner une image solaire circulaire à la base, avait été utilisée. Le centre de cette image circulaire a été observé, et a donné l’altitude directe du centre du Soleil. On attribue généralement à Ibn Junis le mérite de cette amélioration de l’astronomie arabe. (G. Bigourdan, « Les Cadrans Solaires. » Annuaire du Bureau des Longitudes, 1918, p. 258.)
Avant cette époque, les Arabes avaient l’habitude d’utiliser le gnomon simple, et ils appliquaient une correction pour le demi-diamètre du Soleil. C’est clairement le cas pour les observations d’Al Battani, comme nous le constatons par la latitude de Rakka dérivée de ses observations. Dans cette recherche, j’ai traité toutes les observations solaires arabes antérieures à celles d’Al Khujandi et d’Ibn Junis comme ayant été faites avec le gnomon simple, ou un autre instrument de projection d’ombre, tel qu’un quadrant mural, avec lequel le bord de l’ombre, correspondant au bord supérieur du Soleil, a été observé. Cette méthode a nécessité une correction, appliquée par les observateurs arabes, pour le demi-diamètre du Soleil, comme on le voit dans les observations d’Al Battani.
L’estimation ptolémaïque du demi-diamètre du Soleil était de 16 pieds 9 pouces, et les astronomes arabes ne semblent pas avoir beaucoup modifié cela. Al Fargani a obtenu 31 2/5 minutes d’arc pour le demi-diamètre apparent du Soleil à sa distance la plus proche de la Terre, de sorte que son demi-diamètre, selon lui, était de 15' 42". Une valeur proche de celle ptolémaïque est donnée par d’autres observateurs arabes.
J’ai utilisé le demi-diamètre ptolémaïque pour reconstituer les observations arabes en général, antérieures à Al Khujandi et Ibn Junis.
(3) Parallaxe solaire : la parallaxe horizontale moyenne du Soleil (c’est-à-dire le déplacement du soleil à l’horizon, vu par un observateur à la surface de la Terre, par rapport à sa position par rapport au centre de la Terre) est de 8. 8, selon les mesures exactes modernes. Les Arabes, cependant, comme Ptolémée avant eux, ont utilisé une valeur beaucoup plus grande pour la parallaxe solaire, dépendant d’une estimation erronée de la distance du Soleil à la Terre. Voici les estimations arabes de la parallaxe solaire (Dreyer, « Planetary Systems », 1906, p. 257)
| Observateur | Distance du Soleil en demi-diamètres de la Terre | Parallaxe horizontale du Soleil |
| Al Fargani |
1220
|
2’ 49”
|
| Al Battani |
1146
|
3’ 0”
|
| Abu’l Faraj |
1260
|
2’ 44”
|
| MÉCHANT |
1209
|
2’
51”
|
Ptolémée avait adopté 1210 rayons terrestres pour la distance du Soleil, ce qui correspond à la parallaxe solaire 2' 51". (La mesure moderne de la distance du Soleil est de 93 millions de miles, ou 23 491 rayons terrestres, correspondant à la parallaxe solaire de 8".8.)
Il est clair, d’après les diverses estimations des astronomes arabes, qu’ils ont fait des mesures pour vérifier l’estimation de Ptolémée, et la méthode adoptée a donné le même résultat moyen. Cependant, Ibn Junis (1000 apr. J.-C.), pour une raison non indiquée, a réduit la parallaxe solaire à 1' 57", et a utilisé cette valeur pour corriger ses propres observations.
D’autres astronomes arabes n’ont pas accepté cette valeur et, après son temps, Ibn Shatir à Damas, en 1363 après J.-C., a utilisé une parallaxe solaire de 2' 59 », et Ulugh Beigh à Samarcande, en 1437 après J.-C., a également utilisé 2' 59 ».
Dans les Éléments de l’astronomie, écrits par Al Fargani, 850 après J.-C., le problème de la parallaxe, tel qu’il s’applique aux positions observées des différents corps célestes, est clairement défini et discuté ; et il est évident que lui et d’autres astronomes arabes comprenaient clairement la nature de ce problème, bien qu’ils ne connaissaient pas la véritable distance du soleil, et par conséquent la véritable quantité de parallaxe solaire. Avant leur temps, les auteurs de commentaires sur l’Almageste de Ptolémée, tels que Proclus, dans les Hypotyposes (vers 450 apr. J.-C.) avaient expliqué en détail le principe de la correction des observations du Soleil, de la Lune et des planètes pour la parallaxe de ces corps.
Les Arabes, à la suite de Ptolémée, croyaient généralement que la parallaxe solaire était une quantité appréciable, près de 3 minutes d’arc, et comme ils souhaitaient vérifier les résultats de Ptolémée aussi précisément que possible, nous pouvons raisonnablement conclure que, en règle générale, ils ont appliqué une correction identique, ou presque identique, à la valeur de Ptolémée pour la parallaxe solaire.
Dans l’Histoire de l’astronomie de Berry (1898, p. 78), il est dit, en référence à « l’école de Bagdad », que « tant d’importance était attachée à des observations correctes, qu’on nous dit que celles qui présentaient un intérêt particulier étaient consignées dans des documents formels, signés sous serment par un corps mixte d’astronomes et d’avocats ».
Ibn Junis déclare avec certitude que son altitude du Soleil, qui est donnée pour les solstices d’été et d’hiver, est « corrigée de l’effet de la parallaxe, qui la diminue ».
Je ne suis cependant pas en mesure de trouver une preuve directe similaire que tous les astronomes arabes aient appliqué cette correction ; et, comme il semble possible, et même probable, que certains d’entre eux aient donné des résultats pour l’Obliquité sans le faire, j’ai montré, dans le graphique général des résultats de l’Obliquité Arabe [à la fin de ce chapitre] la valeur à la fois avec et sans correction (dans la plupart des cas la correction ptolémaïque) pour la parallaxe.
Il est possible que certains astronomes arabes aient été influencés par Hipparque, qui n’a pas pu trouver de parallaxe pour le Soleil, et a laissé le problème non résolu. (Voir Dreyer, Planetary Systems, 1906, p. 184) D’autres, se sentant peut-être incertains de la quantité exacte de parallaxe du Soleil, ont pensé qu’il valait mieux donner leurs résultats sans cette correction. Dans certains cas, lorsque l’altitude du Soleil aux deux solstices est donnée, la latitude obtenue à partir des observations donne un indice sur la question de savoir si la correction de parallaxe ptolémaïque a été appliquée ou non.
Comme le montrent les observations d’Al Battani, 880 apr. J.-C., la latitude de Rakka obtenue de ses observations n’est que de 2' 8" plus élevée que la latitude moderne, 35° 57' N., si l’on suppose qu’il n’a pas appliqué cette correction. Cette différence, de 2 pi 8 po, doit être un peu plus réduite, car les ruines qui marquent le site de Rakka au moyen âge se trouvent à une certaine distance au nord du village moderne de Rakka. D’autre part, s’il utilisait la correction de parallaxe ptolémaïque, alors la latitude donnée par ses observations serait de 3' 39" plus élevée que la latitude moderne, mais sujette à une petite réduction pour le site médiéval. Ces chiffres laissent la question, dans l’ensemble, assez indéterminée, mais avec la probabilité en faveur de la non-application de la correction de parallaxe ptolémaïque par Al Battani.
Des remarques similaires s’appliquent aux observations faites par Abul Wafa à Bagdad en 987 après J.-C., et la latitude obtenue à partir des observations d’Abul Wafa n’est que de 2' 2" plus élevée que la latitude moderne de Bagdad (33° 21' N.) si nous supposons qu’il n’a pas utilisé la correction de parallaxe solaire ptolémaïque ; mais, s’il l’utilisait, l’erreur de latitude serait plus grande, à savoir 3' 28" plus élevée que la latitude moderne de Bagdad. La probabilité semble donc être qu’Abul Wafa n’a pas appliqué de correction pour la parallaxe.
Ibn Junis, au Caire en l’an 1000 après J.-C., est le premier astronome arabe qui déclare expressément qu’il a appliqué une correction pour la parallaxe solaire, en plus de donner les détails des observations estivales et hivernales de l’altitude du Soleil. Les observations sont citées par Laplace, comme suit (extrait du chapitre XI de l’œuvre d’Ibn Junis) :
J’ai mesuré la plus grande déclinaison, et j’ai trouvé 23°35', ce qui rend la parallaxe du soleil différente de celle qui est rapportée par Ptolémée, comme je l’expliquerai dans ce tableau. J’ai trouvé avec les instruments de notre Seigneur le Prince des Croyants, Aliziz-Billah-Nazar-Aboul-Mansour, l’altitude du Soleil à midi, corrigée de l’effet de la parallaxe, qui la diminue, 36° 21' 30", le soleil étant alors au premier degré du Capricorne.
J’ai pris cette mesure avec toute la précision et tout le soin possible. J’ai trouvé de même l’altitude corrigée de l’effet de la parallaxe au commencement du cancer, lorsqu’elle était à son maximum, 83° 31' 30". En soustrayant la plus petite de ces deux altitudes de la plus grande, nous obtenons 47° 10', dont la moitié ou la plus grande déclinaison est de 23' 35". C’est ce que j’ai adopté dans ce tableau.
J’ai aussi comparé un grand nombre de fois l’altitude des méridiens au commencement du Cancer et du Capricorne avec les altitudes correspondantes avant et après midi, et j’ai trouvé qu’elles s’accordent avec la plus grande déclinaison que j’ai observée ; pour cette raison, je peux garantir son exactitude. C’est pour cette raison que j’ai choisi ces deux points de l’écliptique, parce que, s’il y avait une erreur de plusieurs minutes à la place du Soleil, cela ne produirait aucune différence sensible, le changement de déclinaison étant alors très faible.
On nous informe qu’Ibn Junis a réduit la parallaxe solaire ptolémaïque à 1' 57" (chapitres inédits d’Ibn Junis revus par Delambre, Histoire de l’Astronomie du Moyen Age, page 101. Voir aussi Dreyer, Planetary Systems, p. 261.)
En ce qui concerne le gnomon utilisé par Ibn Junis pour ces observations, il est dit dans l’Encyclopédie de l’Islam, par Houtsma, (Vol III, p. 537) que "Ibn Junis a découpé un sillon, sur le côté du gnomon, qui se terminait par une cavité hémisphérique. Dans la rainure, un fil était suspendu au sommet du gnomon, avec un poids en forme de boule. Lorsque le gnomon est perpendiculaire, celui-ci se pose dans le creux. Le nivellement, au moyen de l’eau, de la surface sur laquelle l’ombre tombait est également décrit.
Comme mentionné précédemment, en relation avec les corrections arabes pour le demi-diamètre du Soleil, Ibn Junis a utilisé un gnomon avec une plaque au sommet, ayant un trou central, de manière à donner une image circulaire du Soleil, dont le centre pouvait être facilement déterminé. Après avoir recalculé les observations d’Ibn Junis et appliqué des corrections modernes pour la parallaxe et la réfraction, nous obtenons l’obliquité corrigée de 23° 36' 11 » à partir de ses observations, et la latitude de son observatoire 30° 05' 0 ». On pense que le site de l’observatoire d’Ibn Junis, où les observations ont été faites, se trouve près de la mosquée du sultan El Hakem. C’est à 1' 26 » au nord du centre du Caire, et c’est donc à 30° 03' 30 » de latitude. L’erreur de latitude d’après les observations de gnomons d’Ibn Junis n’était donc que de 1' 30".
Une autre observation arabe digne d’une mention spéciale est celle d’Al Khujandi, car nous avons une excellente description de l’instrument qu’il a utilisé (voir « Manuscripts of Bagdad Astronomers » par le Dr M.C. Johnson, dans Observatory vol. LIX, p. 224). Cet instrument était un « sextant géant », d’un rayon de 60 pieds, dont la circonférence était divisée en degrés et en minutes, et chaque minute en dix parties, à 6 secondes d’intervalle.
Une image solaire a été formée sur la circonférence, par l’éclairage d’une ouverture à sténopé au centre, et un disque solaire artificiel marqué d’axes perpendiculaires a été ajusté à l’image pour déterminer la coïncidence exacte entre le centre du disque et la division de l’échelle. Un grand soin a été apporté à l’orientation, au nivellement et au centrage de l’image. Pour l’Obliiquité, il obtint 23° 32' 21".
Malheureusement, il n’existe aucune déclaration sur les corrections qu’Al Khujandi a appliquées à ses observations. Mais comme il s’agit d’une valeur particulièrement petite par rapport à d’autres de la même période, notamment Ibn Junis, il est raisonnable de déduire qu’Al Khujandi, tout comme Ibn Junis, a appliqué une correction pour la parallaxe solaire, mais a probablement utilisé la valeur ptolémaïque. L’obliquité corrigée alors trouvée à partir de ses observations, en utilisant les corrections modernes, serait de 23° 33' 55".
Autres valeurs d’obliquité déterminées par les astronomes arabes et perses entre 830 et 1019 apr. J.-C.
En plus des résultats précédents, le tableau suivant donne les valeurs de l’obliquité enregistrées par d’autres astronomes arabes et persans jusqu’en 1019 après J.-C. ; et j’ai montré les résultats obtenus en corrigeant la parallaxe, la réfraction et le demi-diamètre du Soleil, lorsque cela est nécessaire, dans la colonne 7, en supposant que la parallaxe ptolémaïque a été utilisée, et dans la colonne 8, en supposant qu’aucune parallaxe n’a été utilisée par l’observateur arabe.
[Note de Setterfield : Dodwell fait référence à un tableau ici, et c’était évidemment son but initial, mais ce qu’il a fini par faire, c’est le graphique comme montré à la fin de ce chapitre. Sous le graphique, nous avons noté comment il a marqué les mesures qui contenaient la correction et celles qui ne l’étaient pas.]
Celles-ci sont principalement tirées d’une liste obtenue par le Dr M.C. Johnson, à Birmingham, de diverses sources faisant autorité, ainsi que d’autres trouvées dans l’Encyclopédie de l’Islam de Houtsma, et d’une liste donnée par E. Bernard, et publiée dans Philosophical Transactions of the Royal Society, Londres, abrégé Vol III, p. 75 (1684 A.D.). J’ai rejeté des observations manifestement entachées d’erreurs graves, telles que celles attribuées à Al Kwarizmi, 23° 51' (2) (en plus de son résultat précédent 23° 35'), Ibn al Alam 23° 40' et Rustam 23° 51', (2) ainsi que les premières tentatives des astronomes arabes entre 776 et 786 après J.-C. 23° 31'.
Il est dit, dans l’Encyclopédie de l’Islam, vol. III, p. 535, décrivant le gnomon tel qu’il était utilisé par les Arabes, qu’il s’agissait d’une « tige perpendiculaire, souvent avec un sommet en forme de cône ». Si l’on utilisait ce type de gnomon à sommet conique, cela donnerait une valeur d’Obliquité trop faible, (voir Chapitre 2) avec un cône de 90° au sommet, une correction de +1'.7 est nécessaire à l’obliquité déterminée avec celui-ci ; 80° en haut, +2'.4 ; 70° en haut, +3'.4 ; et 60° en haut, +4'.6.
Les résultats arabes, cependant, suggèrent que, en général, le gnomon à sommet plat a été utilisé, après la première courte période d’observations ; Mais la faible valeur enregistrée au stade le plus ancien, 23° 31', correspond à l’utilisation d’un gnomon en forme de cône.
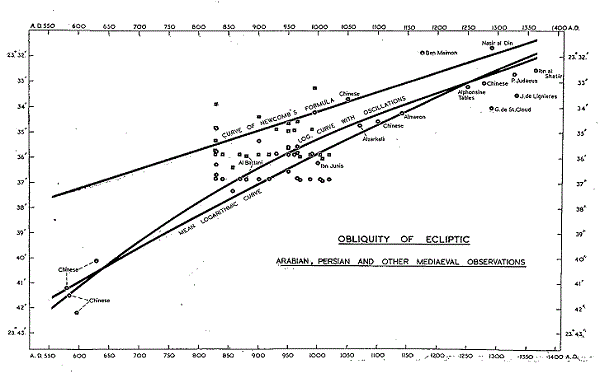
L’obliquité pour la date moyenne du tableau suivant, 916 apr. J.-C., selon la formule de Newcomb, est de 23° 34' 49" ; et selon la Nouvelle Courbe, oscillation comprise, elle est de 23° 36' 12". Si nous admettons que certaines des observations arabes ont été corrigées pour la parallaxe ptolémaïque, et que d’autres ne l’ont pas été, et aussi que, probablement dans la première partie de la période, un gnomon à sommet conique a pu parfois être utilisé, alors la valeur moyenne observée de l’obliquité s’accorderait plus étroitement avec la nouvelle courbe qu’avec la formule de Newcomb. Comme on peut le voir sur la figure suivante, la courbe d’oscillation tend à rapprocher les observations de la période arabe de la position correspondant à la formule de Newcomb. De plus, on peut voir d’un coup d’œil que la formule de Newcomb ne satisfait pas aux observations, prises dans leur ensemble, au cours de cette période.

Les carrés sont les données brutes et les cercles les valeurs corrigées
*********************