à partir de http://www.astromeyer.de/Bilder/artikel/dreistab.jpg
CHAPITRE 7
OBSERVATIONS MÉDIÉVALES ET MODERNES DE L’OBLIQUITÉ DE L’ÉCLIPTIQUE
Ceux-ci sont tirés en partie du Mémoire de Wendelin (Solis Obliquitas), et en partie de sources telles que l’Encyclopaedia Britannica, 9e édition, article « Astronomy », Hutton’s Mathematical and Philosophical Dictionary, vol. 1, p. 455, l’article « Ecliptic », la liste des obliquités contenue dans Ball’s Astronomy, page 354, la liste des déterminations d’obliquité de E. Bernard, mentionnée précédemment, et d’autres sources auxquelles il sera fait référence.
OBSERVATIONS MÉDIÉVALES DE L’OBLIQUITÉ DE 1020 À 1600 APRÈS JC
Au début du XIe siècle, le développement de la recherche astronomique s’est répandu de l’Est vers l’Europe, et a été particulièrement encouragé en Espagne, à la fois parmi les Maures et les princes espagnols, en particulier Alphonse X de Castille, qui a employé plusieurs astronomes notables à Tolède, où il a préparé les Tables Alphonsiennes. Parmi ces astronomes se trouvait Al Zarkali (Arzachel), qui a déterminé l’obliquité de l’écliptique à Tolède en 1070 après J.-C. Ses observations solstitielles, ainsi que quelques autres mentionnées, selon la déclaration de Wendelin, sont consignées comme suit :
Arzachel le Maure, vers notre an 1070, remarqua que la déclinaison du soleil ne dépassait pas 23° 34', et Almaéon, qui le suivit en l’an 1140, observa 23° 33 1/2', puis Prophatius Judaeus, en l’an 1328, ajouta à cela 23° 32'...
On donne un grand appui aux observations de ces auteurs, quand on compare la décrémente, ce qui est excessivement constant à cette époque, et surtout parce qu’ils n’utilisaient pas le calcul des parallaxes, mais déterminaient leurs obliquités à partir des altitudes maximale et minimale du soleil, de sorte qu’ils ne se trompaient pas au-delà d’un total de 2' ; mais par-dessus tout, la diligence très louable d’Almaeon brille en ce qu’il voulait qu’ils soient plus sûrs à la demi-minute près.
Al Zarkali
Lorsque les observations d’Al Zarkali sont corrigées pour les valeurs modernes
de parallaxe et de réfraction, nous obtenons le résultat suivant :
Al Zarkali, 1070 apr. J.-C., Tolède, latitude 39°
51' N., longitude 4° 0' O. : obliquité corrigée 23° 34' 42"
Almaeon
Les observations d’Almaeon nécessitent également les corrections
modernes pour la parallaxe et la réfraction. Le résultat corrigé est le
suivant :
Almaeon 1140 A.D. Tolède, latitude 39° 51' N.,
longitude 4° 0' O. : obliquité corrigée 23° 34' 12"
Ben Maimon
E Bernard, Philosophical Transactions 1684,
dit
Le savant Juif, Rabbi Moyses Ben Maimon, A.D., 1174, a trouvé l’Obliquité 23° 30'. Comme il s’agit de l’une des valeurs basses, il est probable, comme indiqué précédemment, que Ben Maimon ait appliqué des corrections pour la valeur ptolémaïque de la parallaxe solaire et du demi-diamètre.
En
tenant compte de cela, et en utilisant des valeurs modernes pour la
parallaxe, la correction au centre du soleil et la réfraction, nous
obtenons
Ben Maimon, 1174 apr. J.-C., Cordoue, latitude 37°
52' N., longitude 4° 48' O. : obliquité corrigée 23° 31' 51".
Tables alphonsiennes, préparées à partir
d’observations à Tolède
La valeur de l’obliquité obtenue à partir de ces observations est donnée
dans l’Encyclopédie de l’Islam (Houtsma, Vol
III, page 503), à savoir 23° 32' 29". Cette valeur est dérivée des
observations faites par les astronomes de Tolède, et une correction
totale de + 42" pour la parallaxe et la réfraction doit être appliquée,
comme dans le cas d’Al Zarkali. Nous avons ensuite les
Tables Alphonsiennes, 1250 A.D. Latitude 39° 51'
N., Longitude 4° 0' O. : Obliquité corrigée 23° 33' 11"
Nasir Al Din
L’Obliquité trouvée par Nasir al Din, en 1290 apr. J.-C., 23° 30' est
donnée dans la liste de E. Bernard, (Philosophical
Transactions, 1684), également dans le Dictionnaire de
Hutton. En corrigeant cette valeur pour la parallaxe ptolémaïque et le
demi-diamètre du soleil utilisés par Nasir al Din, et en appliquant les
corrections modernes, y compris la réfraction, nous obtenons
Nasir Al Din, 1290 A.D. Maragha (Perse), latitude
37° 21'N., longitude 46° 17'E. : obliquité corrigée 23° 31' 40".
Guilliame de Saint-Cloud
L’obliquité obtenue à partir des observations de Saint-Cloud est donnée
dans l’Astronomie médiévale, par J.L.E
Dreyer, dans les Études de C. Singer sur
l’histoire et la méthode de la science, Vol II. À la page 117, se
référant à l’Almanach de Saint-Cloud pour 20 ans à partir de 1292 après
J.-C., il dit : « D’après les altitudes
soltitielles observées du soleil en 1290, l’obliquité de l’écliptique
est de 23° 34', et la latitude de Paris, de 48° 50' N. » (Remarque.
La latitude réelle de l’Observatoire de Paris est de 48° 50' 11" N.)
Guillaume de Saint-Cloud, 1290 ap. J.-C., Paris,
latitude 48° 50' N., longitude 2° 20 E. : obliquité 23° 34'
Jean de Lignières
L’Obliquité obtenue par de Lignières est donnée dans un compte rendu de
son œuvre par G. Bigourdan dans Comptes Rendus,
1915, 20 décembre, pages 753-754. A propos de son Obliquité, 23° 31'
45", Bigourdan cite ci-après une lettre écrite par Wendelin à Gassendi,
(Gassendi, Opus VI. 428) :
… et remarquez-moi qu’en 1332 l’obliquité de l’écliptique était de 23° 31' 45". Ce résultat n’a pas pu être obtenu à Paris, où la réfraction hivernale diminue la distance des deux tropiques. Se pourrait-il que le Provincial ait pu lui-même faire venir de la province à Paris le résultat qu’il attribue à Lignières ?
Bigourdan dit qu’il n’y a aucune raison de croire que ce fut le cas,
mais que cette valeur rapportée de l’Obliquité doit être considérée
comme ayant été obtenue à Paris par Jean de Lignières. Il ressort de la
déclaration de Wendelin que l’obliquité obtenue par de Lignières n’a pas
été corrigée pour la réfraction. En appliquant cette correction, et la
valeur moderne de la parallaxe, nous obtenons
Jean de Lignières, 1332 apr. J.-C. Paris. Latitude
48° 50' N., Longitude 2° 20' E. : Obliquité corrigée 23° 33' 31".
Ibn al Shatir
La valeur de l’Obliquité trouvée par Ibn al Shatir, 23° 31', est donnée
dans l’Encyclopédie de l’Islam, Vol. III,
page 503. Il est également donné par E. Bernard, dans Philosophical
Transactions, 1684 A.D., comme suit :
Ibn Shatir Damascenus, anno 1363, dit qu’il a corrigé l’Obliquité, la faisant 23° 31', sans négliger la parallaxe horizontale du soleil, qu’il dit avoir trouvée de la quantité extraordinaire 2° 59'. (Il s’agit évidemment de 2' 59", le même que celui utilisé 74 ans plus tard par Ulugh Beigh.)
Nallino, dans son article sur l’astronomie arabe dans l’Encyclopédie
de l’Islam, vol. 1, page 499, dit : « Au
Caire, Ibn al Shatir a fait de bonnes observations ; ses tables étaient
renommées en Syrie, en Égypte et dans toute l’Afrique du Nord. D’après
les observations d’Ibn al Shatir, en appliquant des corrections modernes
au lieu de celles qu’il a utilisées, nous avons
Ibn al Shatir, 1363 apr. J.-C., Le Caire, latitude
32° 04' N., longitude 31° 17' E. : obliquité corrigée 23° 32' 32".
Ulugh Beigh
Selon le dictionnaire mathématique de Hutton, Ulugh
Beigh, petit-fils de Tamerlan, a construit de très grands instruments à
son observatoire de Samarcande, dans le Turkestan, en particulier un
quadrant d’environ 180 pieds de hauteur. Avec cet instrument, en 1437
après J.-C., il a trouvé que l’altitude du centre du soleil, corrigée de
la valeur de la parallaxe qu’il utilisait (parallaxe horizontale 2'
29 ».4), était de 73° 52' 54 » au solstice d’été, et de 26° 52' 20 » au
solstice d’hiver. Lorsque la valeur moderne de la parallaxe est
utilisée, au lieu de celle adoptée par Ulugh Beigh, et avec des
corrections également pour la réfraction, nous obtenons
Ulugh Beigh, 1437 A.D., Samarcande, latitude 39°
39' 40 » N., longitude 66° 59' E., altitude 2150 pieds, obliquité
corrigée 23° 31' 44 »
LES ASTRONOMES EUROPÉENS MÉDIÉVAUX
Purbach et Regiomontanus
Vers 1460 apr. J.-C., l’obliquité de l’écliptique fut observée à Erfurt
et à Nuremberg (Nuremberg) par George Purbach, éminent astronome et
mathématicien de Vienne, et par son assistant élève, Johannes Müller,
qui devint plus tard l’astronome le plus célèbre de son temps en Europe,
et fut appelé Regiomontanus, de Mons Regius ou Königsberg, où il est né
en 1436 après J.-C. Selon Wendelin, Purbach et Regiomontanus ont fait
des observations de l’Obliquité vers l’an 1460 après J.-C., à Erphordia
(Erfurt), latitude 51° 0' N, longitude 11° 01' E., en Allemagne
centrale, et aussi à Nuremberg, latitude 49° 27' 31 » N., longitude 11°
01' E. Wendelin déclare qu’au premier endroit, « ils
ont trouvé la déclinaison maximale du soleil 23° 28', et l’intervalle
des tropiques 46° 56', mais si les parallaxes qu’ils soustraient sont
rétablies, alors l’intervalle est porté à 46° 57' 55" à peu près, et
c’était la distance vue de leurs propres yeux.
En
utilisant les valeurs modernes de parallaxe et de réfraction, nous avons
Purbach et Regiomontanus, 1460 après J.-C., Erfurt,
latitude 51° 0' N, longitude 11° 01' E. Obliquité corrigée 23° 30' 24".
Purbach et Regiomontanus (suite) Observations
à Nuremberg
Wendelin affirme en outre que Purbach et Regiomontanus ont trouvé la
distance zénithale observée du soleil à Nuremberg 24° 56 1/2' . En
utilisant la latitude de Nuremberg 49° 27' 31 », et en appliquant des
corrections pour la parallaxe et la réfraction, nous obtenons de cette
observation
Purbach et Regiomontanus, 1460 apr. J.-C.,
Nuremberg, Obliquité corrigée 23° 30' 38 ».
Selon Clavius dans Opera Math. Tome III page 149, cité dans l’Astronomie de Ball, page 354, Regiomontanus a observé l’Obliquité en l’an 1460 après J.-C., à Vienne, avec un quadrant. Comme Purbach et Regiomontanus étaient rattachés à l’Université de Vienne à cette époque, il a été suggéré que les observations précédentes à Erfurt et à Nuremberg ont pu être obtenues par des observateurs assistants, sous leur direction.
L’obliqité trouvée à Vienne, et donnée dans l’Astronomie de Ball, est évidemment la valeur corrigée. L’obliquité moyenne pour l’année 1460 est donc la suivante
| L’obliquité en 1460 apr. J.-C. | |
| Erfurt | 23° 30’ 24” |
| Nuremberg | 23° 30’ 38” |
| Vienne | 23° 30’ 49” |
| Obliquité moyenne | 23° 30’ 37” |
Toscanelli
Paolo Toscanelli aurait construit son célèbre gnomon dans la cathédrale
de Florence dans le but de démontrer la variation de l’obliquité de
l’écliptique, qui avait longtemps été soupçonnée. La méthode de mesure
de l’altitude du soleil avec le gnomon consistait à faire entrer la
lumière du soleil par la fenêtre sud de la lanterne au-dessus du dôme de
la cathédrale, et à la faire passer par une ouverture de 1,5 pouce de
diamètre, dans une plaque de bronze, laissée dans le rebord de marbre de
cette fenêtre, puis à noter l’endroit où le long rayon de lumière
frappait le sol du transept nord, environ 350 pieds plus bas.
Le jour du solstice d’été, la lanterne était pourvue d’un revêtement de sol temporaire, ne laissant passer qu’un rayon étroit, tandis que le transept était convenablement assombri pour renforcer l’effet. La position de l’image solaire aux solstices a été tracée sur des dalles solstitielles dans le dallage du sol du transept. Avec cette méthode d’observation, Toscanelli a déterminé l’obliquité à 23° 30' (voir le compte rendu donné par le Dr Parr dans le British Astronomical Journal, 25 juin 1930, vol. 40, n° 8, page 296).
Toscanelli a utilisé la parallaxe ptolémaïque, mais en tenant compte de cela, et en appliquant la correction moderne pour la parallaxe et la réfraction, nous obtenons des observations de Toscanelli
Toscanelli, 1468 apr. J.-C., Florence, latitude 43° 46' N., longitude 11° 20' E. : obliquité corrigée 23° 31' 47".
Walther
Bernhard Walther de Nuremberg, ami et collègue de Regiomontanus de 1475
jusqu’à sa mort en 1504, a effectué 746 mesures d’altitudes solaires
avec un Dreistab et une Regula Ptolemaica [un Triquetrum],
en plus d’un grand nombre d’autres observations astronomiques.
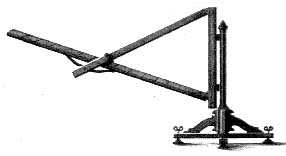
Suivant l’exemple de Regiomantanus, il utilisa un instrument (un Dreistab) composé de trois tiges de bois.

à partir de
http://www.astromeyer.de/Bilder/artikel/dreistab.jpg
La tige verticale était munie d’un fil à plomb et de deux pivots tournants pour les deux autres tiges, qui étaient mobiles en altitude et disposées pour se coucher sur le soleil, avec deux trous de visée afin de déterminer son altitude. L’une de ces tiges mobiles portait des divisions à échelle continue, marquées par centaines jusqu’à 140 000. À partir des cordes mesurées, on a obtenu la distance zénithale correspondante du Soleil, et à partir de là, son altitude a été calculée. (voir E. Zinner, Frankische Sternkunde im bis 16 Jahrhundert).
Wendelin dit que « Bernard Walther, le disciple de Regiomontanus, a laissé de nombreux accords, publiés par écrit, de distances solaires à partir du zénith, dans lesquels pour l’année 1489, et de même 1490, sont ceux qui descendent à 44 895, la corde du sinus entier étant de 100 000. D’où il ressort que la distance observée entre le soleil d’été et le zénith était de 25° 56' 38".
Zinner, cependant, dans l’ouvrage mentionné ci-dessus, donne une analyse complète des nombreuses altitudes solaires observées par Walther au solstice d’été entre les années 1473 et 1503 après J.-C. Ceux-ci sont divisés en quatre groupes, et en appliquant des corrections modernes pour la parallaxe et la réfraction, et en utilisant la latitude de Nuremberg telle qu’elle est donnée dans le Berliner Jahrbuch 49° 27' 31", nous obtenons les obliquités pour les quatre périodes comme suit
|
Année A.D.
|
Obliquité
|
|
1473-78
|
23° 30’ 56”
|
|
1487-95
|
23° 30’ 10”
|
|
1497-1501
|
23° 29’ 52”
|
|
1503
|
23° 31’ 32”
|
Zinner souligne que l’erreur moyenne de l’observation estivale est de
1',02 et qu’elle est réduite à 0,65 si l’on exclut deux observations
discordantes au cours de la période 1487-1501. Si l’on donne un poids de
2 aux observations de 1473-1478 et 1503, et de poids 1 aux observations
de 1487-1495 et de 1497 à 1501, la limite finale pour la date moyenne de
1491 est
Walther, 1491 apr. J.-C., Nuremberg, latitude 49°
27' 31 » N, longitude 11° 02' E. : obliquité moyenne corrigée 23° 30'
50 ».
Novarra
Domenico Maria Da Novarra (1454-1504) était un astronome de l’Université
de Bologne, en Italie, avec lequel Copernic a été associé pendant
environ 3,5 ans, de 1497 à 1500, en tant qu’étudiant, mais « plutôt
en tant qu’ami et assistant qu’en tant qu’élève ». En relation avec
les observations astronomiques de Novarra, on nous apprend qu’en l’an
1491, il détermina l’obliquité de l’écliptique égale à une bagatelle sur
23° 29'. (voir Dreyer’s Planetary Systems,
page 307, et référence à une note dans le manuscrit original de
l’ouvrage De Revolutionibus of Copernicus,
édition 1873, pages 171, 172). Novarra a utilisé la parallaxe
ptolémaïque, et en corrigeant cela à la valeur moderne de la parallaxe,
et en appliquant également des corrections pour la réfraction, nous
obtenons
Novarra, 1491 A.D., Bologne, latitude 44° 29' N,
Longitutde 11° 21' E. : Obliquité corrigée 23° 30' 56"
Johann Werner
En ce qui concerne les observations de Werner à Nuremberg, Wendelin dit
: « En notre année 1514, Werner a observé la
déclinaison 23° 28' 30 » à Nuremberg, et par une correction similaire de
la parallaxe, et la réfraction ajoutée, il en résulte la distance des
tropiques 47° 0' 20 » et de la même manière la déclinaison vraie 23° 30'
10 ». » En appliquant des corrections modernes à celles utilisées
par Wendelin, nous obtenons le résultat suivant des observations
de Werner Johann Werner, 1514 A.D. Nürnberg,
Latitude 49° 27' 31 » N., Longitude 11° 02' E. : Obliquité corrigée 23°
30' 33 ».
Copernic
Copernic est né à Thorn, en Pologne, le 19 février 1473 après J.-C. Il
est admis comme chanoine de la cathédrale de Frauenberg en 1498, mais il
étudie ensuite à l’université de Bologne, en Italie, où il est associé à
Novarra en astronomie pratique. De Bologne, il se rendit à Rome mais
retourna chez lui pour prendre possession de son canonicat à Frauenberg
en 1501. Il retourna ensuite en Italie pour poursuivre ses études, et y
resta jusqu’en 1506, et travailla à Frauenberg jusqu’à sa mort à l’âge
de 70 ans, en 1543 après J.-C. Frauenberg se trouve dans la province
d’Ermland, en Prusse orientale, et se trouve sur la rive sud de la
Frische Haff, golfe de Dantzig.
Dans son grand ouvrage De Revolutionibus Orbium Ceolestium, publié à Nuremberg en 1543, Copernic dit qu’au cours de 30 ans, il avait fréquemment déterminé l’obliquité de l’écliptique. À cette fin, comme mentionné précédemment, l’instrument qu’il utilisait était un Triquetrum, ou « Règle de Ptolémée » (Regula Ptolemaica). C’était huit pieds de hauteur. Il était fait de bois de pin et était divisé par des marques d’encre, les deux bras égaux en 1000 parties, et la règle longue en 1414 parties. Cet instrument était pourvu d’une grande prévoyance, et la latitude obtenue par Copernic pour Frauenberg, où ses observations ont été faites, indique que ces observations ont été faites sur l’ombre projetée par le bord supérieur du Soleil.
Le demi-diamètre du soleil utilisé par Copernic était de 16' 0 » au solstice d’été et de 16' 16 » au solstice d’hiver. Il a également utilisé une parallaxe horizontale moyenne du soleil, 3' 1". Il obtint la latitude de Frauenberg 54° 19' 30 », et l’obliquité de l’écliptique 23° 28' 0 ».
Wendelin dit que la valeur de l’obliquité obtenue par Copernic dépendait des observations faites aux solstices d’été et d’hiver, par lesquelles il a obtenu la distance totale entre les tropiques exactement 46° 56', « n’ayant pas utilisé la bonne proportion de parallaxe, et encore moins celle de réfraction ». À la page 151 de son Mémoire, Wendelin dit que « Copernic ne soupçonnait rien des réfractions hivernales ».
Après
avoir appliqué des corrections modernes pour la réfraction, la parallaxe
et le demi-diamètre, nous obtenons des observations de Copernic
Copernic, 1525 après J.-C., Frauenberg, Prusse
orientale, latitude 54° 20' N. Longitude 19° 41' E. : Obliquité corrigée
23° 30' 30"
(La valeur corrigée de la latitude de Frauenberg, résultant de ces observations, faites par Copernic, est de 54° 21' 15" N.)
La liste des observations de Hutton sur l’obliquité de l’écliptique donne trois valeurs déterminées en l’an 1570 après J.-C., à savoir
23° 29' d’Ignace Dante à Bologne
23° 31' du prince de Hess à Cassel
23° 30' 20" de Rothmann et Byrge à CasselLa moyenne de ces trois valeurs est de 23° 30' 07"
Il n’est toutefois pas certain dans quelle mesure des corrections ont été appliquées à ces résultats, de sorte que, dans l’attente d’investigations plus approfondies, elles ne sont pas utilisées à l’heure actuelle.
Guillaume, prince de Hess, bienfaiteur de l’astronomie à Cassel, aurait érigé le premier observatoire en activité régulière en Europe, à Cassel, sur la rivière Fulda, en l’an 1561. Il prit lui-même une part considérable aux observations, et employa également comme assistants deux astronomes bien connus de cette époque, Christopher Rothmann et Juste Byrge. Cet observatoire était équipé de bons instruments, et les observations ont été publiées à Leyde en 1618 par Snell.
Les observations
de Tycho Brahe
ont été faites à son célèbre observatoire d’Uraniborg, sur l’île de
Huen, latitude 55° 54' 25" N, longitude 12° 42' E, près de Copenhague.
Wendelin dit, à la page 110 de son Mémoire, que Tycho a noté la déclinaison visible du soleil d’été à partir de l’équateur 23° 29' 55 » prenant la latitude de son observatoire à 55° 54' 55 », et par conséquent l’altitude de l’équateur 34° 05' 15 », obtenant ainsi l’altitude estivale observée du soleil 57° 35' 10 ». À cela, Tycho a ajouté une correction de parallaxe de 1' 35" conformément à sa table de parallaxes, dans laquelle la parallaxe horizontale du soleil était prise comme 3', pratiquement la même chose que la valeur de Ptolémée.
En prenant la distance zénithale observée du Soleil en 1587 après J.-C., à 32° 24' 50 », et en appliquant des corrections pour la parallaxe, -5 », et la réfraction +36 », nous obtenons la distance zénithale corrigée du Soleil, 32° 25' 21 ». En soustrayant cela de la latitude (valeur moderne 55° 54' 25 »), nous obtenons l’obliquité, dérivée des observations solstitielles d’été de Tycho Brahe en 1587 après J.-C., 23° 29' 04 ».
Wendelin ne donne pas le résultat des observations solstitielles de
Tycho en hiver, et ne se réfère qu’à l’observation estivale de 1587
après J.-C. Comme il y aurait d’autres observations de l’Obliquité
faites par Tycho Brahe, celles-ci ont sans doute toutes été prises en
compte par des autorités ultérieures. Les valeurs données par ces
autorités, par exemple Encyclopaedia Britannica (9e
édition, article « Astronomie ») 23° 29' 52 », et Ball’s Astronomy,
page 354, 23° 29' 46 », sont à privilégier. La valeur de l’Astronomie de
Ball est celle donnée par Bugge, Berliner Jahrbuch,
1794, page 100.
La moyenne de ces deux valeurs, 23° 29' 49", a été
adoptée dans cette étude.
Edward Wright
Edward Wright était un mathématicien anglais distingué de Cambridge, qui
a apporté de précieuses contributions à la navigation et à l’astronomie.
Il a fait des observations du soleil et des étoiles avec un quadrant de
six pieds dans les années 1594 à 1597 après J.-C. L’obliquité qu’il a
déterminée était de 23° 30' comme indiqué dans la
Table de Hutton de l’obliquité de l’écliptique.
Godifred Wendelin
Wendelin, célèbre astronome belge médiéval, a fait ses observations de
l’obliquité de l’écliptique dans la ville française de Forcalquier, dans
les Basses Alpes. Il dit à la page 15 de son Mémoire que
son instrument était un quadrant, divisé en minutes simples dans les
quadrants. Il était fait de bois, mais si solide qu’en hiver et en été,
il donnait les mêmes distances des étoiles que celles publiées par Tycho
et Kepler.
Il
dit aussi à la page 15, et de nouveau à la page 110, que la déclinaison
apparente ou visible du soleil au solstice d’été était de 23° 30', mais
qu’au solstice d’hiver elle était de 23° 31' 15", toutes deux dépendant
de la latitude 43° 54', qu’il a trouvée à Forcalquier d’après ses
observations des étoiles circumpolaires. C’est-à-dire que sa distance
zénithale observée du Soleil au solstice d’hiver était de 67° 25' 15 »,
et au solstice d’été, elle était de 20° 24' 0 ». En appliquant à ces
observations des corrections modernes de parallaxe et de réfraction,
nous obtenons
Godifred Wendelin, 1609 A.D. Forcalquier, Latitude
43° 57' 34 » N. Longitude 5° 47' 11 » E., altitude 1804 pieds, Obliquité
corrigée 23° 31' 31 »
La différence assez importante entre la latitude observée et la latitude réelle de Forcalquier semble indiquer une combinaison d’erreurs, peut-être d’erreurs d’indice et de gradation du quadrant, ainsi que des erreurs de niveau et de verticalité ; avec la possibilité aussi que le lieu des observations n’ait pas été à Forcalqueir même, mais à une certaine distance de ce centre.
Le résultat de l’obliquité, cependant, ne serait pas affecté par cette erreur dans la latitude adoptée.
Johann Kepler
Les observations faites par ce célèbre astronome ont eu lieu à Linz, sur
le Danube, en Haute-Autriche. La valeur de l’obliquité obtenue d’après
ses observations (Tabulae Rudolphinae, page
116), telle qu’elle est donnée dans l’Astronomie de
Ball, est
Johann Kepler, 1627 A.D., Linz, Latitude 48° 17' N.
Longitude 14° 18' E. : Obliquité 23° 30' 30"
Nicolas Claude de Peiresc
Nocolas Claude de Peiresc était un astronome réputé du début du XVIIe
siècle. Il entreprit, de concert avec Gassendi, de répéter à l’aide d’un
gnomon les observations faites par Pythéas à Marseille, en 326 av.
J.-C., de l’altitude du soleil à midi le jour du solstice d’été, afin de
déterminer jusqu’à quel point l’obliqité de l’écliptique avait changé
depuis l’époque de Pythéas.
Ce qui suit est une traduction d’un extrait d’un article « Sur les Travaux Astronomiques de Peiresc », par G. Bigourdan, dans Comptes Rendus, Académie des Sciences, Paris, 8 novembre 1915, pages 543-545, décrivant les opérations de Peiresc :
Tout en accordant une grande attention à la question des longitudes, dont les erreurs étaient énormes, même à nos portes, Peiresc ne négligeait pas la question de la latitude, comme nous l’avons vu par quelques extraits de ses lettres.
Il recommandait surtout qu’ils soient déterminés par les altitudes méridiennes du Soleil, particulièrement au solstice d’été, en employant un gnomon, qui pourrait alors rivaliser avantageusement, en termes de précision, avec les meilleurs instruments de l’époque.
(L’attention du lecteur est spécialement attirée sur cette déclaration de cet éminent astronome moderne, en ce qui concerne le degré de précision des observations faites avec le gnomon.)
Et il en donna l’exemple lui-même, avec Gassendi, en répétant à Marseille, au solstice d’été de 1636, la mémorable observation de Pythéas.
Déjà l’année précédente, Wendelin l’avait prié de faire cette observation, afin d’élucider la question, à peine effleurée alors, de la variation de l’obliquité de l’écliptique.
Diverses circonstances fortuites ayant retardé cette observation, elle fut faite en 1636. Le choix d’un endroit convenable présentait quelques difficultés. Finalement, il fut décidé d’utiliser l’église du collège de l’Oratoire, alors en construction, où, avec l’accord des autorités religieuses et consulaires, Peiresc fit abattre certaines sections du mur, percer le toit et déplacer une planche.
Voici ce qu’il écrivit à d’Arcos le 20 juillet 1636 :
Nous fîmes préparer un matin une machine de 18 cannes de diamètre, dont le gnomon avait plus de 9 cannes de hauteur, et elle fut divisée en plus de 80 000 parties reconnaissables, de sorte qu’on pouvait reconnaître et déterminer la différence de celle sur laquelle tombait l’ombre solaire précisément, exclusivement à partir des autres parties. soit au-dessus, soit au-dessous. (Cette « canne » était probablement une variante locale de l’ancien taise français, tel qu’utilisé à Marseille, équivalent à 5 1/2 pieds de longueur.)
Et cela fut fait si habilement, et avec si peu de frais, que tous ceux qui étaient présents furent ravis. (Cette dépense était à la charge de la ville, ce qui était donc un prélude aux sacrifices qu’elle faisait généralement par la suite pour soutenir la haute renommée de l’astronomie marseillaise.)
Nous n’avions qu’à percer le toit d’une très haute galerie, de trois ou quatre étages, et recevoir le rayon du soleil en bas, après nous être bien ajustés avec le fil à plomb perpendiculairement à la ligne méridienne, qui était tracée en bas, et avoir enlevé quelques briques à une hauteur de 9 cannes, pour mesurer plus précisément la distance entre le trou dans le toit et la base de l’angle inférieur de la ligne méridienne.
Pythéas n’avait observé qu’avec un gnomon divisé en 600 parties. On trouve que le calcul s’accorde avec celui de Pythéas avec si peu de différence, gagnée successivement par tant de siècles, qu’il sera d’un grand service pour confirmer la certitude des quantités fondamentales qui sont adoptées pour régler tous les mouvements célestes et toute la géographie.
Les observations furent immédiatement communiquées à Wendelin, mais la publication n’eut lieu qu’en 1658, après la mort de Gassendi ; Vous pouvez voir pourquoi c’est le cas ; Requier soupçonne en effet qu’elles n’étaient pas très satisfaisantes.
La hauteur du gnomon était de 51 pieds 8 pouces, 4 lignes, 0 partie, ou 89 328 parties (douzièmes de ligne), et l’ombre s’est avérée être de 31 750 parties, négligeant la réfraction et soupçonnant la parallaxe solaire d’être égale à 20. (Une ligne correspond à un douzième de pouce)
L’altitude solstitielle du centre du soleil s’est donc avérée être de 70° 11' 15".
En prenant 43° 19' 19 » pour la latitude, l’obliquité de l’écliptique a été prise comme 23° 30' 24 ».
La latitude adoptée aujourd’hui (1915) pour Marseille (Ancien Observatoire) est de 43° 17' 52" (1). Nous voyons que les soupçons de Requier n’étaient pas fondés, et que l’observation est remarquablement exacte ; même lorsque « nous comparons les valeurs obtenues à cette occasion pour la latitude de Marseille par les altitudes méridiennes du Soleil, ou de Mars, ou de Saturne, et de diverses étoiles, nous nous étonnons qu’un quadrant à pinnules ait pu donner des résultats si concordants ».
L’Obliquité dérivée des observations de Peiresc est la suivante (le calcul étant donné en entier en raison de l’intérêt qu’elle a, par association avec l’observation antique de Pythéas, 1963 ans avant Peiresc) :
|
Avec les
corrections de Peiresc
|
Avec des
corrections modernes
|
|
|
|
Altitudes observées du bord supérieur du Soleil = 70° 25'
59" Parallaxe utilisée par Peiresc +20 Réfraction utilisée par Peiresc 0 Demi-diamètre du Soleil utilisé par Peiresc -15.04 |
Altitudes observées du bord supérieur du Soleil = 70° 25'
59 » Correction moderne de la parallaxe +3 Correction moderne de la réfraction -19 Correction moderne du centre du soleil - 13' 12 » |
|
a) Altitude
corrigée du centre du Soleil (Peiresc) = 70° 11'
15" (b) Distances zénithales du centre du soleil (Peiresc) = 19° 48' 45" Latitude utilisée par Peiresc = 43° 19' 09" |
Altitude corrigée
du centre du Soleil = 70° 12' 31" a) Distance zénithale du centre du Soleil = 19° 47' 29" b)Latitude approximative du site (Vieux-Marseille) = 43° 17' 52" |
|
Différence (b) – (a) = Obliquité
= 23° 30' 24" |
Différence (b) – (a) = Obliquité
= 23° 30' 23" |
Peter Gassendi
Peter Gassendi était un célèbre philosophe et astronome français. En
1636, il s’associe à Peiresc dans la répétition de la mesure de
l’obliquité de l’écliptique faite par Pythéas en 326 av. J.-C. à
Marseille au solstice d’été. Riccioli (Almagestum
Novum, vol. 1, liv. 3, cap. 14) dit : « Mais
au même endroit, Gassendi se servit d’un gnomon de 52 pieds royaux, et
trouva au solstice d’été l’ombre méridionale de 31 950 unités, dont le
gnomon était de 90 000 ; d’où il en déduisit que l’obliquité de
l’écliptique était la même qu’au temps d’Alexandre le Grand. (2)
Il y a aussi une incohérence dans ce récit, car 52 pieds royaux équivalent à 89 856 unités (52 x 12 x 12 x 12), tandis que 90 000 unités représentent 52 pieds 1 pouce.
Avant 1812 après J.-C., lorsque le pied métrique a été adopté en France, le pied Royal (pied de Roi) ou nourriture de Paris (équivalent à 1,0658 pied anglais) divisé duo-décimal en pouces, lignes et parties, ou douzièmes d’une ligne, était en usage.
Si nous prenons l’affirmation que le gnomon utilisé par Gassendi était de 52 pieds royaux, comparé à la hauteur du gnomon de Peiresc de 51 pieds 8,5 pouces, alors nous obtenons la valeur de l’obliquité presque exactement la même que celle qui a été mesurée par Peiresc.
D’un autre côté, si nous prenons l’affirmation alternative que la hauteur du gonomon était de 90 000 unités, cela donne l’obliquité de 1' 20" supérieure à la valeur de Peiresc, et qui est discordante par rapport à la valeur réelle. L’affirmation selon laquelle le gnomon avait 52 pieds royaux de hauteur est probablement correcte.
L’observation a été faite indépendamment par Gassendi, mais évidemment en un point du bâtiment très voisin de celui utilisé par Peiresc, la différence de hauteur étant exactement celle d’une brique plus une couche de mortier, c’est-à-dire 3 2/3 pouces.
La longueur de l’ombre mesurée par Gassendi est proportionnellement plus longue (à savoir 31 950 – 31 750 = 200 parties, ou 1 pouce, 4 lignes 8 parties, c’est-à-dire très légèrement plus de 1 1/3 pouce) que la mesure de l’ombre de Peiresc. C’est ce que l’on attendrait naturellement de ces hauteurs respectives de gnomon.
Le calcul de l’obliquité déterminée par Gassendi, mais avec une correction moderne, est le suivant :
L’observation de l’obliquité par Gassendi
| L tan altitude du bord supérieur du soleil | = |
L 89856
L 31950 |
||||||||||||||||
| = |
4.9535471
4.5044709 |
|||||||||||||||||
| = |
0.4490762
|
|||||||||||||||||
| = |
L tan 70° 25' 34"
|
|||||||||||||||||
|
|
|||||||||||||||||
| Altitude corrigée du centre du Soleil | = |
|
||||||||||||||||
|
|
|||||||||||||||||
| Différence (b) - (a) = Obliquité | = |
|
Peter Gassendi, 1636 A.D. Marseille, Latitude 43° 17' 52 » N. Longitude 5° 24' E. : l’obliquité moyenne d’après les observations combinées de Peiresc et de Gassendi est de 23° 30' 10 »
NOTE : L’obliquité moyenne obtenue à partir des observations anciennes du Vieux-Marseille en 326 av. J.-C., est de 23° 54' 20 », ce qui donne une diminution de 24' 10 » au cours des années 1963 jusqu’à l’époque de Peiresc et Gassendi.
De plus, la latitude du Vieux-Marseille dérivée des observations anciennes est de 43° 18' 25 », ce qui n’est que 33 » au-dessus de la valeur moderne. C’est une confirmation frappante de l’exactitude de ces anciennes observations.
J.B. Riccioli
Joannes-Baptiste Riccioli, astronome, philosophe et mathématicien
italien, est l’auteur de l’Almagestum Novum,
jusqu’à présent le plus grand ouvrage médiéval sur l’astronomie. Il a
fait des observations sur l’obliquité de l’écliptique, et deux résultats
sont donnés, le premier en 1636 après J.-C., 23° 30' 20", cité dans l’Encyclopaedia
Britannica, 11e édition, article sur l’astronomie ; aussi dans le
Hutton’s Mathematical and Philosophical Dictionary,
vol. 1, page 455, article « Ecliptic ». Une autre valeur est donnée dans
ce dernier ouvrage pour l’année 1655 apr. J.-C., à savoir 23° 29'.
J.B. Riccioli, 1650 A.D. Bologne, latitude 44° 30'
N., longitude 11° 21' E. : la moyenne de ces deux, l’obliquité moyenne,
23° 29' 40"
Johannes Hevelius
Johannes Havelius était un célèbre astronome et bourgmestre de Dantzig,
sur la côte baltique de la Prusse orientale. Parmi ses nombreuses
observations, citons celles de l’obliquité de l’écliptique, et
les valeurs données pour Dantzig, latitude 54° 22'
N., longitude 18° 39' E., sont
1653 -- 23° 30' 20 » Hutton’s
Mathematical Dictionary
1660 -- 23° 29' 10 » Encyclopaedia
Britannica
1661 -- 23° 28 » 53 » (corrigé) Hutton’s
Mathematical Dictionary
Jean Dominique Cassini
Jean Dominique, la première des quatre générations de Cassinis à occuper
le poste de directeur de l’Observatoire de Paris, dès sa création en
1671, était d’abord professeur de mathématiques et d’astronomie à
Bologne, en Italie. En 1653, il fut autorisé par le Sénat de
l’Université de Bologne à corriger et à fixer la ligne méridienne de
l’église Saint-Pétrone de Bologne, qui avait été tracée par Toscanelli
en 1575.
En
l’absence des rapports de ses observations à Paris, qui sont contenus
dans les archives de cet Observatoire, il n’est possible d’énoncer ici
que les valeurs de l’Obliquité qui lui sont attribuées en 1655 à
Bologne, 23° 29' 15 » (Hutton) et en 1672 ap. J.-C., à Paris, 23° 29'
0 » (Encyclopaedia Britannica, 11e édition).
Il s’agit clairement des valeurs corrigées, et à partir d’elles, nous
obtenons pour la période
moyenne Jean Dominique Cassini, 1655 ap. J.-C.,
Bologne, latitude 44° 30' N., longitude 11° 21' E., et 1672 ap. J.-C.,
Paris, latitude 48° 50' N. Longitude 2° 20' E. : Obliquité moyenne (1664
ap. J.-C.) 23° 29' 08"
ADDITIONNEL L’OBLIQUITÉ RÉSULTE DE 1660 APRÈS J.-C. À NOS JOURS
À partir de l’époque de l’établissement des observatoires de Paris et de Greenwich, en 1671 et 1676 après J.-C., respectivement, les valeurs de l’obliquité de l’écliptique données par diverses autorités sont les valeurs corrigées selon la liste suivante, à l’exception de Wurtzelbaur, 1686 après J.-C., dont les altitudes méridiennes observées du soleil aux solstices d’été et d’hiver de cette année-là sont données par Edmond Halley, le second astronome royal d’Angleterre, dans un article publié dans les Philosophical Transactions of the Royal Society de Londres, 1687 A.D., Vol 16, n° 190, page 403 (Vol III, page 407 dans les Transactions abrégées).
Dans cet article, la distance observée du zénith d’été du centre du soleil est de 25° 57' 30 », et la distance du zénith d’hiver observée est de 72° 52' 50 ». En utilisant des corrections modernes pour la parallaxe et la réfraction, nous obtenons l’obliquité corrigée 1686 après J.-C. 23° 28' 58"
La latitude de Nuremberg (où les observations ont été faites), calculée à partir de ces observations, est de 49° 26' 50 », ce qui se compare très favorablement à la valeur moderne de cette ville, 49° 27' 31 ».
*******************
L’obliquité résulte de 1660 à 1868 apr. J.-C.
| Date ap. J.-C. | Observateur | Obliquité | Différence (1) | Autorité (2) |
| 1660 | Montons | 23° 29' 03" |
+2"
|
Hutton |
| 1660 | Hevelius | 23° 29' 10" |
+9"
|
Ency. Brit. |
| 1661 | Hevelius | 23° 28' 52" |
-9"
|
Hutton |
| 1672 | Cassini | 23° 29' 0" |
+5"
|
Ency. Brit. |
| 1672 | Plus riche | 23° 28' 52" |
-3"
|
Hutton |
| 1686 | Wurtzelbauer | 23° 28' 58" |
+ 10"
|
Halley (3) |
| 1686 | La Hire | 23° 28' 52" |
+ 4"
|
Hutton |
| 1689 | Flamstead -5 (4) | 23° 28' 56" |
+ 9"
|
L’astronomie de Ball |
| 1690 | Flamstead | 23° 28' 48" |
+ 1"
|
Ency. Britannique |
| 1690 | Flamstead | 23° 29' 0" |
+ 13"
|
Hutton |
| 1703 | Bianchini | 23° 28' 35" |
- 6"
|
Ency. Britannique |
| 1703 | Bianchini | 23° 28' 25" |
- 16"
|
Hutton |
| 1706 | Roemer | 23° 28' 41" |
+ 2"
|
Hutton |
| 1715 | Louville | 23° 28' 24" |
- 11"
|
Hutton |
| 1730 | Godin | 23° 28' 20" |
- 8"
|
Hutton |
| 1736 | Condamine | 23° 28' 24" |
- 1"
|
Ency. Brit. |
| 1743 | Cassini de Thury | 23° 28' 26" |
+ 4"
|
Ency. Brit. |
| 1750 | Lacaille | 23° 28' 19" |
0
|
Ency. Brit. |
| 1750 | Bradley | 23° 28' 18" |
- 1"
|
Hutton |
| 1755 | Bradley | 23° 28' 15" |
- 1"
|
Ency. Brit. |
| 1756 | Mayer | 23° 28' 16" |
0
|
Ency. Brit. et Hutton |
| 1769 | Maskelyne | 23° 28' 10" |
0
|
Ency. Brit. et Hutton |
| 1772 | Hornsby | 23° 28' 08" |
0
|
Hutton |
| 1779 | Almanach nautique | 23° 28' 07" |
+ 2"
|
cité par Hutton |
| 1780 | Cassini | 23° 27' 54" |
- 10"
|
Ency. Brit. |
| 1795 | Maskelyne | 23° 27' 58" |
+ 1"
|
L’astronomie de Ball |
| 1800 | Almanach nautique | 23° 27' 50" |
- 5"
|
cité par Hutton |
| 1800 | Maskelyn | 23° 27' 57" |
+ 2"
|
Ency. Brit. et Hutton |
| 1800 | Piazzi | 23° 27' 56" |
+ 1"
|
Ency. Brit. et Hutton |
| 1800 | Étang | 23° 27' 56" |
+ 1"
|
Hutton |
| 1800 | Delambre (5) | 23° 27' 57" |
+ 2"
|
Ency. Brit. et Hutton |
| 1800 | Bessel | 23° 27' 55" |
0
|
L’astronomie de Ball |
| 1812 | Astronomes anglais et pères | 23° 27' 42" |
-7"
|
Hutton |
| 1813 | Étang | 23° 27' 49" |
0
|
Ency. Brit. |
| 1813 | Brinkley | 23° 27' 50" |
+ 1"
|
L’astronomie de Ball |
| 1813 | Arago et Mathieu | 23° 27' 49" |
0
|
Subvention (6) |
| 1815 | Bessel | 23° 27' 48" |
0
|
Ency. Brit. |
| 1816 | Brinkley | 23° 27' 49" |
+ 1"
|
Ency. Brit. |
| 1825 | Pearson | 23° 27' 44" |
+ 1"
|
Ency. Brit. |
| 1835 | Aéré | 23° 27' 40" |
+ 1"
|
Ency. Brit. |
| 1850 | Leverrier | 23° 27' 32" |
0
|
Ency. Brit.
|
| 1868 | Aéré | 23° 27' 22" |
- 1"
|
L’astronomie de Ball |