CHAPITRE 4
ANCIENNES OBSERVATIONS HINDOUES
Tournons-nous maintenant vers les anciennes observations
hindoues des ombres solstitielles du soleil. Nous verrons
comment ils confirment les résultats chinois précédents.
Très tôt, les anciens hindous utilisaient un gnomon vertical
pour observer les ombres solaires, de la même manière que les
Chinois utilisaient cet instrument. Le Surya Siddhanta, l’un des
ouvrages astronomiques les plus importants de l’Inde ancienne,
décrit l’observatoire hindou de cette époque. Il se compose
principalement d’un plan horizontal plat, d’un sol ou d’une
terrasse de Chunam, qui est une chaux faite de coquillages, et
qui, une fois sèche, est dure et capable de recevoir un
polissage égal à celui du marbre. Sur la surface du sol de
Chunam, nivelé avec de l’eau, un cercle est décrit, et une tige
verticale de longueur donnée est érigée au centre comme un
stylet ou un gnomon, et au moyen de la longueur et de la
direction de son ombre, projetée sur le plan par le soleil, une
variété de problèmes astronomiques est résolue.
La plus ancienne mention de l’obliquité de l’écliptique,
déterminée par les anciens hindous, est décrite par C.P.S. Menon
dans son livre Early Astronomy and Cosmology.
Il est tiré du traité d’astronomie jaïn appelé Suryaprajnapti.
Ce texte contient des estimations de dimensions, telles que la
taille des corps célestes, et des orbites du soleil et de la
lune, et les hauteurs de leurs orbites.
On peut déduire de la nature des observations que les anciens
Hindous, comme les Chinois dont le système de cosmologie et de
mesure astronomique était similaire, utilisaient un gnomon de 8
pieds de hauteur et mesuraient la longueur des ombres projetées
par celui-ci.
Les chiffres qui sont donnés permettent de déterminer la
longueur de ces ombres aux solstices et aux équinoxes. Ces
chiffres sont en accord avec la « cosmologie carrée » des
anciens hindous. (Voir fig. 7) Il est clair qu’ils sont dérivés
de mesures des ombres projetées par le gnomon.
Dans cette « cosmologie carrée », la terre était considérée
comme reposant sur une base carrée, avec les diagonales pointant
nord-sud et est-ouest, et s’élevant sous la forme d’une pyramide
vers le pôle nord. La base de la pyramide terrestre s’étendait
jusqu’aux « quatre coins (ou quartiers) de la terre », et elle
s’élevait jusqu’au « toit du monde » et au « mont Meru, au
sommet duquel vivaient les dieux ». On croyait que dans la
région de Meru, « le jour des anges qui habitent Meru dure six
mois, et leur nuit aussi six mois ». (De toute évidence, cela
représente la région polaire nord). Certains pensaient que Meru
était l’un des sommets enneigés de l’Himalaya.
L’Inde (Bharata), avec Ceylan à ses pieds, était considérée,
dans le Suryaprajnapti, comme le quart le plus méridional de la
terre, et le quart nord était une autre terre habitée, (Airavata),
tandis que les quartiers est et ouest étaient considérés comme
des terres inhabitées.
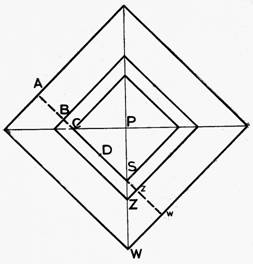
GRAPHIQUE 7
L’ancienne « cosmologie carrée »
hindoue (projection polaire de la terre, assumée comme d’une
forme pyramidale)

Sur cette figure :
P est la projection polaire du pôle nord de la Terre sur le plan d’observation.La diagonale, PSZW, est la projection du méridien, et l’autre diagonale est la ligne est-ouest.
S représente le point sur la terre verticalement au-dessous du soleil à midi au solstice d’été
Z représente le point sur la terre verticalement au-dessous du zénith au point d’observation.
W représente le point sur la terre verticalement au-dessous du soleil à midi le solstice d’hiver.
CS est égal au « diamètre » de l’orbite solstitielle d’été du soleil, et équivaut à 99 640 yojanas.Bz est égal au « diamètre » du Jambu-dvita (la terre), = 100 000 yojanas.
Aw est égal au « diamètre » de l’orbite solstitielle hivernale du soleil, = 100 660 yojanas.
De ces chiffres,
DS = 49 820 yojanas.
Dz = 50 000 yojanas.
Dw = 50 330 yojanas.Et
Dz - DS = Sz = 180 yojanas.
Dw - Dz = ZW = 330 yojanas.La distance le long du méridien, SZ et SW, est donc de
SZ = 180 Ö 2 = 254,556 yojanas.
ZW = 330 Ö2 = 486.642 yojanas.
Celles-ci représentent les équivalents proportionnels des
longueurs d’ombre projetées aux solstices d’été et d’hiver par
un gnomon vertical, tout comme dans le cas analogue des
anciennes observations chinoises. Ils représentent également des
distances sur la terre correspondant aux distances célestes des
points immédiatement au-dessus d’eux, sur la base que « le char
du soleil se déplace à une hauteur de 800 yojanas au-dessus du
sol ».
Compte tenu de la similitude essentielle entre les anciens systèmes chinois et hindous, il semble très probable que les anciens hindous utilisaient également un gnomon de 8 pieds de haut. La base géométrique pour le calcul de l’obliquité et de la latitude du lieu d’observation, correspondant à ces chiffres dans le Suryaprajnapti, est indiquée sur la figure 8.
FIGURE 8
Observations de l’obliquité de l’écliptique, d’après les
chiffres donnés dans le traité d’astronomie jaïn appelé
Suryaprajnapti.
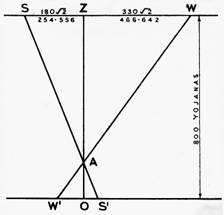
Lieu des observations : Ceylan
Date des observations : environ 945 av. J.-C.
À partir des triangles similaires AZS, AOS' et AZW, AOW',
nous avons pour
hauteur du gnomon................................... AO = 8 pieds
de longueur de l’ombre solstitielle d’été..... OS' = 2,54556 pieds
de longueur de l’ombre du solstitiel d’hiver......... OW'= 4,66642 piedsCes chiffres donnent pour l’obliquité, après application de corrections pour les réfractions, la parallaxe solaire et la réduction au centre du soleil :
Obliquité = 24° 11′ 04"Et pour la latitude du lieu d’observation :
Latitude = 8° 18′ 32" N.
Le circuit quotidien du soleil autour de la terre était considéré comme rectangulaire. On pensait que le soleil, en se levant à l’est, se déplaçait vers le haut en ligne droite jusqu’au méridien, et de là en ligne droite jusqu’au point de couchage ouest. Sa trajectoire était donc parallèle aux faces de la pyramide de terre, et à une distance constante de 800 yojanas (équivalent à 3784 miles) du sol.
On croyait que « le mouvement des corps célestes est rectiligne,
les formes circulaires de leurs trajectoires quotidiennes
n’étant qu’une illusion causée par leur grande distance ».
Ces idées firent apparaître aux anciens Hindous que la géométrie
du gnomon vertical, et des ombres qu’il projetait du soleil,
était proportionnelle aux distances célestes, en supposant que «
le char du soleil se déplace à une hauteur de 800 yojanas
au-dessus du sol ».
Une estimation similaire a constitué la base des anciennes
mesures chinoises. Selon le Chou Pei,
« l’image du Ciel est un parasol qui enveloppe ; Celui de la
terre est un bassin renversé. Le ciel est séparé de la terre par
une distance de 80 000 li. Cette distance de 80 000 li
correspondait à 4090 milles, presque la même que l’ancienne
estimation hindoue de la distance du soleil. Le soleil,
cependant, dans le système chinois, était considéré comme se
déplaçant en cercles, s’élargissant progressivement et diminuant
en altitude, du solstice d’été au solstice d’hiver.
Les chiffres donnés dans le Suryaprajnapti se réfèrent à deux endroits où des observations ont été faites. En plus de l’obliquité de l’écliptique à la date de l’observation, la latitude des sites des observations peut également être calculée. (Fig. 8)
L’obliquité de l’écliptique, ainsi
déterminée, après correction de la réfraction et de la parallaxe
solaire est de 24° 11' 4".
La latitude du premier lieu
d’observation, pour lequel les
longueurs d’ombre aux deux solstices sont disponibles, est de 6°
18' 32" nord. Cela indique un endroit à Ceylan à environ 22
miles au nord de Dondra Head, (latitude 5° 56' Nord), le point
le plus méridional de Ceylan. Comme le fait remarquer M. Menon,
nous pouvons conclure que ces anciens astronomes hindous «
considéraient l’extrémité sud de la terre comme se trouvant à la
latitude 6° N. Incidemment, nous remarquons que des astronomes
avaient été envoyés à Ceylan même à cette époque reculée pour
observer les solstices. »
Le deuxième lieu d’observation : Une seule observation, à savoir celle du solstice d’hiver, est donnée. Nous pouvons cependant l’utiliser pour calculer la latitude. L’énoncé de l’observation laisse place à deux sites alternatifs. L’un d’eux se trouve à la latitude 20° 15' 04" nord, à 14 milles au sud de Cuttack, près du sommet de la baie du Bengale ; et l’autre est à 10° 33' 41" de latitude N, correspondant à la latitude de Trichur, 10° 32' N, dans la province de Cochin du sud-ouest de l’Inde. Cet endroit est le plus probable, car il ne nécessiterait qu’une courte expédition côtière dans le sud de Ceylan.
On dit que le Suryaprajnapti a été écrit "vers le 5ème siècle avant J.-C., mais le système cosmologique décrit dans l’ouvrage, à part quelques éléments incongrus ajoutés à celui-ci, est certainement d’une date beaucoup plus ancienne, à une époque lointaine de l’antiquité où les hommes n’avaient pas encore commencé à considérer le cercle comme la courbe parfaite, ou comme fournissant une échelle de mesure angulaire.
D’après l’Astronomie hindoue de Brennand, une révision notable de l’astronomie fut faite vers 945 av. J.-C., à l’époque des célèbres princes Rama et Dasaratha, sous lesquels l’étude de l’astronomie reçut beaucoup d’encouragement et fut cultivée avec beaucoup d’attention.
Rama était le fils de Dasaratha, et est le héros du grand poème épique hindou appelé le Ramayana. Le Ramayana fait référence à la conquête d’une partie de Ceylan par le héros Rama et ses partisans, qui, selon le poème, assiégèrent et prirent la capitale de son roi Rawana. Aucune occupation permanente du pays n’a été faite à cette époque, mais 400 ans plus tard, en 543 av. J.-C., Vijaya, un prince indien, est arrivé du continent avec une petite armée et s’est établi comme le seul dirigeant de Ceylan.
Bentley affirme, dans son Hindu Astronomy, qu’à l’époque de Rama, à l’équinoxe d’automne, « on trouva par observation que les Colures (1) étaient retombées par rapport aux étoiles fixes de 30° 20' depuis les premières observations de 1192 av. J.-C. »
Ce mouvement est cohérent avec le mouvement de précession de la terre dans l’intervalle de 247 ans, et il est en outre dit que « Dans la même période de 247 ans et un mois, ils ont constaté que la lune avait fait 3303 révolutions, et un signe terminé, qu’il y avait aussi 3056 lunaisons de périodes synodiques, et le nombre de jours dans toute la période était de 90245.5. »
Brennand commente : « Il n’y a rien d’improbable en ce qui concerne les observations ainsi énoncées. C’est exactement le genre d’observations que les astronomes hindous faisaient constamment, pour déterminer les jours où le soleil était à l’équinoxe ou au solstice - ces quatre jours de l’année où des sacrifices et des offrandes devaient être faits à l’Être suprême - observations qui, comme l’a exprimé Laplace, ont abouti à "l’exactitude remarquable des mouvements moyens qu’ils (les Hindous) ont attribués au soleil et à la lune, et nécessitait nécessairement des observations très anciennes.
L’ancienne observation hindoue de
l’obliquité de l’écliptique rapportée dans le Suryaprajnapti, et
décrite dans ce chapitre, se situe presque exactement au milieu
entre les observations chinoises de 1120 av. J.-C. et de 700 av.
J.-C. Ces trois résultats forment un groupe cohérent, tant en
termes de quantités que de durées. De plus, ils sont tout à fait
conformes aux résultats ultérieurs des observations chinoises,
hindoues et grecques.
Valeur hindoue de l’obliquité
dérivée du Surya Siddhanta (environ
510 av. J.-C.)
La valeur de l’obliquité généralement attribuée aux anciens Hindous d’une période postérieure à la précédente est de 24° 0'. C’était à une époque où il y avait eu des progrès considérables dans la théorie et la pratique de l’astronomie par rapport aux temps plus reculés. Cette valeur de 24° 0' est donnée par Brennand dans Hindu Astronomy pp. 80 et 236, et est tirée des énoncés mathématiques de l’ancien manuel d’astronomie hindou, Surya Siddhanta.
C’est l’un des ouvrages astronomiques les plus connus des
Hindous qui soient parvenus jusqu’à nos jours, et il est écrit
en langue sanskrite. On comprend, d’après ses propres
déclarations, qu’il a été compilé à la fin de la période connue
sous le nom de Trita Yuga, et qu’il incarne la science de
l’astronomie telle qu’elle était à cette époque ; certains
changements ayant été apportés depuis des temps plus anciens.
La fin du Trita Yuga correspond à 510 av. J.-C. On pense que le
site des observations est Hastina Pura, l’ancien siège du
gouvernement en Inde, à la latitude 28° 38'N, à quelques
kilomètres au sud de Delhi.
La valeur de l’obliquité, selon l’ancienne pratique, était
déterminée à partir des altitudes maximale et minimale du soleil
à midi aux solstices d’été et d’hiver, non corrigée pour la
parallaxe solaire, la réfraction et le demi-diamètre du soleil.
Avec ces corrections ajoutées, le résultat final est 24° 00'
44". Si l’on se reportera à la figure 2, on verra combien cette
valeur s’accorde avec la courbe de 510 av. J.-C. Comme le reste
des anciens résultats chinois et hindous, il diffère
considérablement de la valeur calculée à partir de la formule de
Newcomb, à savoir 15' 16" plus élevé que cette valeur.
***********************