CHAPITRE 3

OBSERVATIONS CHINOISES ANCIENNES

Notre connaissance des observations astronomiques chinoises est due en grande partie à P. Gaubil, S.J. (1689-1759 après J.-C.), qui était un missionnaire français en Chine. Il a extrait un nombre considérable d’observations solstitielles chinoises de nombreuses sources documentaires. Il les étudia à fond et les communiqua aux astronomes européens dans ses Lettres édifiantes, publiées par Souciet en 1732. Selon Léopold de Saussure, « le missionnaire P. Gaubil, S.J., qui s’est donné tant de mal pour informer les astronomes européens sur l’astronomie chinoise, était d’un esprit curieux, modeste et d’une grande honnêteté. »

En 1734, P. Gaubil envoya un important manuscrit à l’astronome français De Lisle, donnant les résultats de ses recherches astronomiques concernant les constellations et les catalogues chinois des étoiles fixes, le cycle des jours, les solstices et les ombres méridiennes du gnomon observées en Chine. Soixante-quinze ans plus tard, au début du XIXe siècle, Laplace, reconnaissant la valeur unique de cet ouvrage, le sauve de l’oubli et publie, dans la Connaissance des Temps de 1809, la partie traitant des solstices et des ombres méridiennes du gnomon observées en Chine.

Au total, les observations solstitielles chinoises qui sont disponibles consistent en une précieuse série de 26 observations des altitudes de midi du soleil aux solstices d’été et d’hiver, s’étendant sur 2380 ans, de 1100 av. J.-C. à 1280 apr. J.-C. Elles étaient considérées comme des observations importantes du point de vue chinois, et ont été faites par des astronomes officiels des différentes périodes, dont plusieurs noms nous sont parvenus. Aussi, ils ont été faits dans les capitales de la Chine ou les résidences du souverain dans les différentes dynasties.

Ce fait jette une lumière favorable sur l’exactitude des observations, parce que les latitudes qui en découlent s’accordent remarquablement avec les latitudes vraies de ces capitales. Il s’agissait de :

Toutes ces observations, à l’exception de celles faites par Ko-chou-King à Pékin à l’époque de Kubilaï Khan, ont été faites avec le gnomon vertical, fixé par la loi en Chine à une hauteur standard de 8 pieds chinois, ce qui était égal à 8 pieds 9 pouces en mesure anglaise. Ko-chou-King, dans le but d’obtenir la plus grande précision possible, se servit d’un gnomon de 40 pieds de hauteur, surmonté d’une plaque de cuivre, percée d’un petit trou, de manière à donner un point rond de lumière, dont le centre était mesuré avec précision et la longueur de l’ombre enregistrée avec précision.

Nous pouvons nous demander pourquoi une telle attention a été accordée à la mesure des ombres solaires sur une si longue période de l’histoire chinoise ? La réponse donnée par P. Ricci est que les Chinois, dans leur système social, religieux et gouvernemental, attachaient une importance particulière au calendrier et aux observations célestes nécessaires à son maintien exact. (1) C’était parce que l’année civile chinoise était une année lunaire et ne correspondait pas aux saisons. Tous les changements dans le ciel étaient considérés comme ayant une influence directe sur la vie terrestre et étaient soigneusement observés.

Les saisons astronomiques, avec les changements de végétation qui les accompagnaient, étaient les plus évidentes, et « la relation harmonieuse existant entre le ciel et la terre était considérée comme s’étendant même au domaine de la morale ». C’était le principal devoir de l’Empereur « de faire connaître les conditions de cette harmonie, c’est-à-dire d’indiquer les limites des saisons et la situation de l’année terrestre ou civile par rapport à l’année céleste ou astronomique ».

À cette fin, il employa de nombreux astronomes qui étaient responsables devant lui de faire les observations et de calculer les éphémérides. L’empereur, de son côté, était tenu pour « responsable devant le ciel, et s’il négligeait le calendrier, non seulement il causait des désagréments au peuple, mais il était considéré comme coupable d’une irrévérence qui diminuait sa vertu et mettait en danger la dynastie ».

Il était donc nécessaire à la fois à l’Empereur et à ses ministres et astronomes de veiller à ce que les observations soient faites avec le plus grand soin possible et qu’elles soient maintenues tout au long de l’Antiquité et du Moyen Âge. P. Ricci a déclaré en 1605 après J.-C. que le roi chinois gardait plus de 200 personnes à grands frais pour calculer les éphémérides chaque année.

Les premières observations astronomiques chinoises sont contenues dans le Chou-Pei-Soan-King (« le livre sacré des calculs appelé Chou-Pei »). Ce livre est un livre composite, et on pense qu’il a été compilé pour la première fois sous sa forme actuelle au 4ème ou 5ème siècle avant JC. La partie la plus ancienne donne les résultats d’observations faites dès 1120 av. J.-C., mais une section relative à l’observation d’une étoile circumpolaire (Suen-Ki), à laquelle sont associées les observations au méridien des ombres solaires aux solstices d’été et d’hiver, a été montrée par l’astronome chinois Kao-Kiun (anciennement de l’Observatoire Zo-se, près de Shanghai) pour correspondre à la date de 700 av. J.-C.

Une traduction française complète du Chou-Pei, avec notes, a été publiée par Edouard Biot dans le Journal Asiatique, Paris, 1841. Dans une préface chinoise au Chou-Pei, écrite en 1213 après J.-C., il est dit :

« Cette œuvre date d’une époque à mi-chemin entre les dynasties Chang et Chou. Après que Chou Kung eut reçu les instructions de Chang-Kao (le grand préfet)(2), les hommes de l’époque de Chou ont conservé sa mémoire en appelant la combinaison Chou-Pei (gnomon ou stylet dans un cercle), afin de désigner le gnomon.

Le mot Pei signifie techniquement un gnomon vertical, et il semble d’après cette déclaration que le Chou Pei a été nommé ainsi en l’honneur du célèbre prince Chou Kung, frère de Wu Wang (fondateur de la dynastie Chou, environ 1120 av. J.-C.), qui est renommé en Chine à travers tous les siècles suivants pour sa sage législation et son intérêt pour la science astronomique.

Dans le Chou-Pei, les résultats sont donnés dans deux systèmes de mesure, circulaire et linéaire. Les mesures circulaires donnent une valeur plus grande pour l’obliquité de l’écliptique, et sont d’une date antérieure, probablement vers 1120 av. J.-C. Ils sont clairement basés sur des mesures des ombres solaires aux solstices d’été et d’hiver.

Dans la première partie du Chou-Pei où Chou Kung reçoit des instructions du grand préfet, Chang-Kao, il est dit que « le ciel se mesure en degrés ». Les Chinois divisaient le cercle en 365 degrés, chaque degré correspondant à la quantité du mouvement quotidien moyen du soleil dans l’année. Pour une mesure plus fine, le cercle a également été divisé en 714 000 li circulaires. Ainsi, chaque li circulaire équivalait à environ deux secondes d’arc, soit 1/1800 de degré (européen).

Pour les besoins du calcul, les Chinois ont subdivisé le li en 300 pou. Pour d’autres calculs utilisés en relation avec les mouvements célestes, le pou a été divisé en 1461 (c’est-à-dire 3651/4 x 4) parties. Ainsi, un diplôme chinois équivalait à 1954 li, 247 et 933/1461 pou.

Dans les instructions données dans le Chou Pei pour dessiner un cercle (sur une plate-forme nivelée) pour représenter le cercle du ciel, il est dit "pour correspondre au cercle du ciel, qui est de 365 degrés, divisez soigneusement le cercle tracé sur le sol. Qu’il n’y ait pas la plus petite différence entre les degrés. Des instructions sont ensuite données pour diviser ce cercle en quatre quadrants, et il est déclaré que « chacune des quatre parties de la circonférence comprendra 91 5/16 degrés ». Les mesures auraient été faites avec l’aide d’un officier appelé Ta-tsiang (grand charpentier).

La valeur la plus ancienne de l’obliquité de l’écliptique, donnée par le Chou Pei, est indiquée dans les termes suivants :

"Kien-nieou (le tropique du Capricorne) est éloigné du pôle Nord 115 degrés 1695 li, 21 et 819/1461 pou. Le Tsing oriental ou Tong-tsing (le tropique du Cancer) est éloigné du pôle Nord 66 degrés 1481 li, 155 et 1245/1461 pou.

En convertissant ces chiffres en degrés européens, nous obtenons :

Ainsi, les deux affirmations donnent l’obliquité de l’écliptique à la date la plus ancienne du Chou Pei (environ 1120 av. J.-C.) comme étant de 24 degrés 12 minutes 6 secondes.

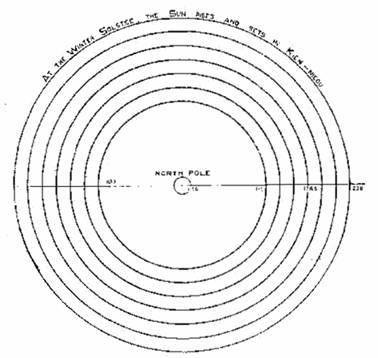
Ces résultats chinois les plus anciens ont été obtenus par calcul, basé sur des observations faites avec le gnomon, et la méthode est énoncée dans le texte du Chou Pei. On donne un schéma d’une projection polaire du ciel, reproduite ici (Fig. 6), montrant les « Sept Cercles appelés Heng ».

Graphique 6

Schéma des Sept Cercles appelés Heng

[les mots disaient : « Au solstice d’hiver, le soleil se lève et se couche à Kien-Nieou. » Le nombre au milieu sous le pôle Nord est 11,50. La marque à gauche sur le bord du cercle intérieur est 103. En allant vers la droite à partir de la marque du pôle Nord, après 11.50 se trouvent 119, 178.5 et 238]

Comme il est dit au début du livre que le ciel est mesuré en degrés, et que ces degrés sont également donnés des valeurs en li circulaire, à raison de 714 000 li à 3651/4 degrés chinois (360 degrés européens), il est clair que les rayons projetés des sept cercles représentent la mesure circulaire. Le cercle intérieur du groupe des sept, marqué 119, a un rayon de 119 000 li circulaires et est la projection polaire du cercle de 60 degrés (européen) de distance polaire nord. (714000/119000 x 360° = 60°) Les autres cercles sont espacés de 10 degrés, c’est-à-dire à des distances polaires de 70°, 80°, 90°, 100°, 110° et 120°.

Il s’agissait des cercles fondamentaux de l’astronomie chinoise, dont le cercle médian de 178 500 rayons circulaires (distance polaire nord de 90° européen) représente l’équateur. La position du soleil aux solstices d’été et d’hiver est liée aux cercles intérieur et extérieur de 119 000 li (60° européen) et de 238 000 li (120° européen), par la quantité ± (30° - obliquité). De toute évidence, il s’agissait d’une mesure purement solaire, et n’avait aucun rapport en soi avec la distance polaire d’une étoile circumpolaire, mais par une heureuse coïncidence, il y avait, à l’époque du Chou Pei, une étoile circumpolaire, Kappa Ursae Minoris, qui était à la même distance (30° - obliquité), égale alors à 5° 47' 54'', soit 11 500 li circulaires chinois du pôle Nord. C’était ce qu’on appelait « la pierre précieuse » (comme la « pierre suprême » de la supposée « pyramide terrestre », qui, selon l’ancienne cosmologie chinoise et indienne, était reliée de manière invisible au point pivot central du ciel).

La règle donnée dans le texte du Chou Pei pour obtenir les distances polaires du soleil aux solstices d’hiver et d’été, est la suivante :

« Placez le cercle extérieur à une distance de 238 000 li du pôle (il s’agit du processus de calcul par la boîte de calcul, la casserole, utilisée avec des billes pour les calculs arithmétiques), soustrayez le rayon du Suen-ki (l’étoile circumpolaire, ou « la pierre précieuse »), égal à 11 500 li, le reste est de 226 500 li. Faites-en le dividende. *1

Celui-ci est ensuite divisé par le nombre de li et les parties d’un li égal à un degré chinois, à savoir 1954 li 247 et 933/1461 pou. Le résultat de cette division donne 115°, 1695 li, 21 et 319/1461 pou, comme indiqué précédemment (européen, 114° 12' 6 » ; et, en soustrayant 90°, l’obliquité est donc de 24° 12' 6 »).

De la même manière, la règle donnée pour le solstice d’été est la suivante :

« Placez le cercle intérieur à une distance de 119 000 li du pôle, ajoutez le rayon du Suen-ki, égal à 11 500 li. Cela représente un total de 130 500 li. Faites-en le dividende.

Celui-ci est ensuite divisé par le nombre de li dans un degré chinois, comme précédemment ; et le résultat de la division donne 66° 1481 li, 155 et 1245/1461 pou (européen, 65° 47' 54 », et, en soustrayant cela de 90°, l’obliquité est, comme précédemment, de 24° 12' 6 »).

La différence entre 226 500 li (la distance polaire nord du tropique du Capricorne) et 130 500 li 2 (la distance polaire nord du tropique du Cancer) donne pour la distance intertropicale totale, soit deux fois l’angle d’obliquité, 96 000 li (mesure circulaire chinoise). Cela équivaut à 48° 24' 12" (européen).

De là, nous obtenons l’obliquité moyenne, 24° 12' 6".

Il faut bien comprendre que ces anciens calculs, qui définissent les positions des tropiques du Capricorne et du Cancer, et donc l’obliquité de l’écliptique à cette époque, dépendaient d’observations réelles des ombres solaires projetées par le gnomon vertical. Il n’y avait pas d’autre moyen de connaître les positions solstitielles du soleil que par ces observations.

Ils se rapportent à la date d’environ 1120 av. J.-C. et ont été fabriqués dans l’ancienne capitale chinoise de Mo. Cette ville était située sur la rive occidentale de la rivière Hoang-ho, à environ 35° 35' de latitude nord et 115° 40' de longitude est, dans ce qui est aujourd’hui la province de Shantung. Dans l’Atlas historique et commercial de la Chine du Dr Albert Hermann (Volume 1, Série de monographies de l’Institut Harvard – Yen-Ching, Harvard University Press, Cambridge, Massachusetts, États-Unis, 1935), il y a une carte à grande échelle de ce district, montrant le centre originel de la Chine ancienne, avec les sièges des dynasties et leurs dates avant J.-C., selon la chronologie traditionnelle. La ville de Mo est représentée comme le siège de la dynastie Chang et a été la résidence royale de 1198 à 1122 av. J.-C.

La latitude de Mo, mesurée sur cette carte, est de 35° 35' N., et elle était à environ 16 milles au nord de la ville actuelle de Tsao-chow. Cela correspond au temps et à l’itinéraire empruntés par Wu-Wang, premier empereur de la dynastie Chou, pour voyager avec son armée depuis sa capitale Hao-King (aujourd’hui Sian-fu). Après avoir traversé la rivière Hoang-ho près de Loyang, il avança vers la plaine à l’extérieur de la capitale (c’est-à-dire Mo), de Chou, le dernier empereur de la dynastie Chang, où ce dernier fut vaincu. Sur ce, il s’enfuit vers sa capitale (Mo), mit le feu à son palais de Lou T’ai et périt dans les flammes. (voir Variétés Sinologiques, Shanghai, n° 52, pages 172, 173.)

Cette obliquité de l’écliptique, obtenue comme ci-dessus directement d’après les observations chinoises, décrites dans le Chou Pei, à savoir 24° 12' 6", n’a pas été corrigée pour la réfraction et la parallaxe solaire, qui étaient inconnues des anciens observateurs. Lorsque ces corrections sont appliquées, l’obliquité corrigée de l’écliptique, donnée par le Chou Pei pour environ 1120 av. J.-C., est de 24 degrés 13 minutes 56 secondes. C’est 24 minutes 17 secondes de plus que l’obliquité donnée par la formule de Newcomb pour la même date.

L’étude des erreurs d’observation avec le gnomon, donnée dans le chapitre 2 précédent, montre clairement qu’une différence aussi grande, équivalente aux trois quarts du diamètre du soleil, ne peut pas être expliquée comme due à une erreur d’observation. Il s’agit d’une différence réelle entre l’obliquité réellement observée de l’écliptique à la date de 1120 av. J.-C. et la valeur théorique calculée au moyen de la formule de Newcomb.

Ce résultat est particulièrement remarquable parce qu’il s’agit de la plus ancienne observation astronomique directe de l’obliquité de l’écliptique que nous ayons. La grande différence par rapport à la formule de Newcomb est confirmée par les longueurs des ombres solaires à midi aux solstices d’été et d’hiver données dans la dernière partie du Chou Pei, correspondant à l’an 700 av. J.-C.

De ceux-ci, nous obtenons l’obliquité de l’écliptique 24° 1' 58". C’est 15 pi 8 po de plus que la valeur de 700 av. J.-C., calculée à partir de la formule de Newcomb. Cette différence est équivalente à la moitié du diamètre solaire, et encore une fois, elle est beaucoup trop grande pour être due à une erreur d’observation avec le gnomon. De plus, elle est intermédiaire entre la valeur de Chou Pei pour 1120 av. J.-C. et la série ultérieure d’observations chinoises, qui s’ajustent étroitement sur une courbe, indiquant l’erreur progressivement croissante de la formule de Newcomb à mesure que nous remontons à l’Antiquité.

Le tableau suivant illustre le changement croissant révélé par les observations chinoises à mesure que nous remontons dans l’Antiquité, de 1280 à 1120 av. J.-C.

TABLEAU 2
Différence entre les observations chinoises de l’obliquité de l’écliptique et la formule de Newcomb.
( + plus grand que la formule de Newcomb)
( - plus petit que la formule de Newcomb)

Les grandes différences à l’approche de 1120 av. J.-C. sont frappantes et évidentes. Nous pouvons voir d’un coup d’œil que les données d’observation de l’Antiquité diffèrent fondamentalement de la théorie moderne.

Avant de quitter les observations chinoises, il faut se référer aux longueurs d’ombre (1,5 pied au solstice d’été, et 13,0 pieds au solstice d’hiver, donnant l’obliquité 23° 54' 4"), associées par la tradition chinoise au nom de Chou Kung. Ces longueurs d’ombre se trouvent dans le Chou Li (Livre des Rites) et dans d’autres sources. Il est clair, cependant, qu’ils appartiennent à une date ultérieure à celle de Chou Kung.

Les preuves internes du Chou Pei, ainsi que le grand changement progressif de l’obliquité de l’écliptique donné par les observations chinoises sur une période de 2300 ans, montrent que la valeur la plus ancienne et la plus grande (24° 13' 56"), obtenue du Chou Pei, appartient à l’époque de Chou Kung, vers 1120 av. J.-C. C’est la date de la plus ancienne observation astronomique enregistrée en Chine.

Commentant les longueurs d’ombre de 1,5 pied au solstice d’été et de 13,0 pieds au solstice d’hiver, P. Gaubil a écrit : « Je ne doute pas que des observations aient été faites à partir de l’époque de Chou Kung, mais je ne sais pas si les chiffres qui sont donnés sont très anciens. » (3)

Le regretté Dr Villemarque, directeur de l’observatoire Zo-Se, près de Shanghai, a également exprimé une opinion similaire. Dans une lettre qu’il m’a adressée à ce sujet, il m’a écrit : « Les observations étaient certaines vers 1120 av. J.-C., mais les chiffres ont pu être modifiés au cours des âges. »

Quelque temps après la chute de la dynastie Chou en 249 av. J.-C., l’empereur Che Hwang-ti, de la dynastie Tsin, poussé par des raisons politiques, ordonna de brûler tous les livres en Chine, à l’exception de ceux relatifs à la médecine, à la divination et à l’agriculture. Cela s’est passé en l’an 213 av. J.-C. Après la chute de la dynastie Tsin en 206 av. J.-C., les empereurs de la dynastie Han s’efforcèrent de restaurer la littérature chinoise. Leurs astronomes firent de nouvelles observations des ombres solstitielles solaires, et il est dit que "pendant la période Han (206 av. J.-C. à 265 apr. J.-C.), le gnomon a été perfectionné en le terminant par une plaque de cuivre percée d’un petit trou rond. Au lieu de l’ombre du bord, le centre de la tache lumineuse a été observé. (4)

L’astronome chinois Haui-Nan-Tzu (mort en 122 av. J.-C.) a donné à l’ombre une longueur de 1,5 pied en été et de 13,0 pieds en hiver, comme pour son époque, disons environ 130 av. J.-C. D’après la Nouvelle Courbe, développée dans cette étude, l’obliquité de l’écliptique, correspondant à ces chiffres, appartient plus précisément à 295 av. J.-C., soit 165 ans avant Haui-Nan-Tzu. Mais la différence dans les longueurs d’ombre pour les deux dates n’est pas grande, et il est possible que les mesures de Haui-Nan-Tseu se rapprochent beaucoup des chiffres qu’il donne.

Deux siècles après Haui-Nan-Tzu, il fut représenté à l’empereur Chang-ti, vers 84 après J.-C., que le calcul indiquait certaines erreurs dans le calendrier, qui donnaient des valeurs erronées pour les solstices, les équinoxes et d’autres dates. L’Empereur, « eu égard à ces représentations, ordonna à l’astronome Li-fong de faire un nouveau calendrier. C’est ce qu’il fit, et lui donna le nom de Sse-fen, ou quatre parties. Le tribunal était alors à Loyang.

P. Gaubil dit de ce changement : « Les auteurs de l’astronomie de Sse-fen ont marqué pour Loyang aux deux solstices les ombres observées par Chou-Kung dans la première observation, c’est-à-dire 1,5 pied de solstice d’été, et 13,0 pieds de solstice d’hiver... Ces auteurs ont supposé que l’observation faite par Chou-Kung était inchangée.

Cette déclaration indique que les Chinois n’étaient pas conscients de l’évolution de la valeur de l’obliquité au cours du temps. La confusion était également causée par la différence de longueur des ombres selon la latitude de l’endroit où les observations avaient été faites. C’est pourquoi les observations chinoises ont besoin d’être examinées avec soin. Dans ses notes, P. Gaubil écrit que :

“..... dans les ouvrages astronomiques chinois, nous trouvons les ombres méridiennes du gnomon. Ces types de catalogues sont souvent défectueux et nécessitent un examen ; Il y en a qui ne sont mal calculés que par les astronomes, qui n’avaient aucune idée précise de la trigonométrie sphérique ; il y a des ombres appliquées à tort à des endroits pour lesquels elles ne sont pas appropriées ; dans l’édition des traités d’astronomie de Hoching-tien et Tsou-chong, les ombres méridiennes des deux solstices de Chou Kung sont appliquées à Nankin pour l’année 237 apr. J.-C.

« Les premiers Ouey (Tartares) composèrent un ouvrage astronomique ; leur cour était à Hinchou, une ville près d’un degré plus au sud que Kaifeng-fu. Les ombres solstitielles de Chou-Kung pour Loyang sont de nouveau appliquées à ce Hinchou, du moins à celle du solstice d’été ; Ce qui est fait pour ce lieu est aussi fait pour les autres.

« Dans plusieurs ouvrages d’astronomie chinois, ils ont d’abord donné les ombres solstitielles attribuées à Chou-Kung pour Loyang ; par la suite, d’autres règles sont données pour augmenter ou diminuer la longueur de ces ombres selon que les lieux sont plus au sud ou au nord de Loyang. Ce que je dis ici est clairement marqué dans certains ouvrages astronomiques. Mais dans d’autres, les rédacteurs n’ont pas pris soin de marquer les règles d’augmentation ou de diminution des ombres observées par Chou-Kung afin de trouver les ombres qui correspondent à des lieux plus au sud ou au nord, et de là vient que dans les calendriers pour Nankin ou Hinchou ou d’autres on trouve les ombres pour Loyang.

La confusion concernant les longueurs d’ombre observées par Chou Kung semble avoir pris naissance après l’incendie des livres de la dynastie Tsin à cause desquels de nombreux anciens documents ont été perdus, et il se peut que la nouvelle valeur des longueurs d’ombre à Loyang après cet événement ait été attribuée à Chou Kung comme un hommage de vénération pour sa mémoire.

En ce qui concerne Chou Kung, on dit qu’en plus de l’observatoire où ses observations astronomiques ont été faites, un a également été construit par son frère, l’empereur Wu Wang, fondateur de la dynastie Chou. On l’appelait

"... la Tour des Esprits, parce que tout le peuple de Chou s’est donné avec tant d’empressement à sa construction, qu’elle semblait avoir été élevée par l’enchantement. Le souvenir de ces deux hommes, Chou Kung et Wu Wang, est perpétué dans les annales de la Chine, entouré d’une immense vénération. Longtemps après, les liens politiques et sociaux qu’ils avaient établis furent rompus par les ambitions des chefs d’autres clans, qui profitaient de la faiblesse et des défauts de leurs descendants pour se rendre indépendants du pouvoir central. Confucius, Meng-tsu et tous les historiens, tous les philosophes, les ont représentés comme des princes modèles, et ils n’ont cessé de rappeler le souvenir de leurs institutions aux souverains ultérieurs, comme ayant donné le plus haut degré possible d’ordre, de paix et de bien-être aux populations qui vivaient sous leur gouvernement. Aujourd’hui, après que 3000 ans se sont écoulés, la plupart des bureaux établis dans le Chou-Li survivent encore, les seuls changements étant dans les noms et les fonctions nécessaires pour continuer à les rendre applicables à un empire beaucoup plus vaste, ainsi qu’à une société dans laquelle les conditions de la propriété et de l’état personnel ont été modifiées par le temps.(5)

D’après les preuves maintenant disponibles, nous arrivons à la conclusion que les longueurs d’ombre de 1,5 pied en été et de 13,0 pieds en hiver, à Loyang, ont été obtenues à peu près à l’époque de l’incendie des livres sous la dynastie Tsin, ou peu après, sous la dynastie Han, et ont été attribuées à Chou Kung à cause de la vénération dans laquelle son nom était tenu, et parce qu’on pensait que l’obliquité était restée inchangée depuis son temps. La vraie valeur à l’époque de Chou Kung, cependant, est préservée dans le Chou Pei.

Une analyse attentive de toutes les observations chinoises disponibles montre que la clé des difficultés mentionnées par P. Gaubil réside dans la valeur de la latitude dérivée des observations aux deux solstices. Dans presque tous les cas, cela est très proche de la latitude de l’une ou l’autre des anciennes capitales de la Chine, et confirme l’exactitude générale des résultats chinois.

On peut également déterminer à partir des observations si un gnomon ordinaire projetant une ombre, ou un gnomon avec un trou projetant une tache lumineuse, a été utilisé. L’examen de toutes les observations chinoises confirme également l’exactitude des grandes valeurs de l’obliquité de l’écliptique, obtenues du Chou Pei pour les dates de 1120 av. J.-C. et 700 av. J.-C.

********************

1. La contribution scientifique de Matteo Ricci à la Chine par Henri Bernard, S.J, p. 54. Traduit par Edward Chalmers Werner, Peiping 1935. Retour au texte
2. Probablement l’astronome en chef de la précédente dynastie Chang. Retour au texte
3. Traité de L’Astronomie Chinoise par le P. Gaubil, l c page 39 retour au texte
4. Bulletin n° 125 du Bureau Sinologique, Zikawei, 28 septembre 1932 retour au texte
5. E. Biot. L’Astronomie Indienne et Chinoise, p. 272. Retour au texte

Continuer au chapitre 4