CHAPITRE 9
STONEHENGE
Le grand cercle de pierres de Stonehenge, sur la plaine de Salisbury, dans le Wiltshire, en Angleterre, est l’un des monuments les plus célèbres de l’Antiquité en Grande-Bretagne.

http://www.estatevaults.com/lm/_Stonehenge.jpg
L’astronomie de Stonehenge est d’un intérêt particulier, en raison de la manière dont l’axe du monument est dirigé vers le point du lever du soleil à l’horizon nord-est, à la date du solstice d’été, le 21 juin, de chaque année. Par conséquent, si l’on mesure le relèvement ou l’azimut (l’angle est-nord) de l’axe, on peut calculer la déclinaison correspondante du soleil (c’est-à-dire sa distance à l’équateur céleste dans les cieux), ou, ce qui revient au même, l’obliquité de l’écliptique. À partir de là, nous devrions être en mesure, en utilisant la formule de Newcomb, de trouver très précisément la date à laquelle l’axe de Stonehenge a été établi, c’est-à-dire la date de la construction du monument de Stonehenge, à condition que la formule de Newcomb donne la véritable place du Soleil dans les temps anciens.
Mais, de même que l’étude précédente du Grand Temple Solaire d’Amen Ra à Karnak a montré que la Formule de Newcomb, par elle-même, donne une date si éloignée qu’elle est tout à fait hors de question, de même nous verrons dans cette étude de Stonehenge que la Formule donne de même une date pour sa construction plus de mille ans plus tôt que la date vraie probable. basé sur les recherches archéologiques les plus modernes et les plus approfondies. De plus, on verra que dans les deux cas, lorsque la formule de Newcomb est corrigée pour les effets du mouvement de récupération de l’axe de la terre à partir de sa perturbation antérieure, nous obtenons alors des dates pour Karnak et Stonehenge en accord avec l’histoire et l’archéologie.
L’aspect astronomique de Stonehenge a toujours été d’un grand intérêt public en Grande-Bretagne, et à ce jour, des foules de personnes font un pèlerinage chaque année au monument, et passent la nuit dans un inconfort considérable afin de regarder le soleil se lever sur la « pierre du talon de moine » le jour du milieu de l’été, et d’assister aux cérémonies de l’ordre moderne des druides. Cette orientation vers le point du lever du soleil au milieu de l’été a clairement été réalisée par le ou les concepteurs de Stonehenge avec beaucoup de soin, comme on le verra au cours de cette étude. Il est en accord avec l’architecture remarquable de la partie principale du monument, qui est beaucoup en avance sur les structures plus primitives de Grande-Bretagne, et suggère une date ultérieure à celles-ci.
Sir Norman Lockyer, qui était l’un des plus grands astronomes britanniques de son temps, a publié un livre des plus intéressants en 1906, intitulé Stonehenge and Other British Stone Monuments Astronomically Considered. Il avait auparavant effectué des examens approfondis des temples grecs et égyptiens orientés vers le Soleil et, dans certains cas, apparemment vers certaines étoiles brillantes. Son travail sur le Grand Temple Solaire d’Amen Ra à Karnak, mentionné dans le chapitre précédent, est particulièrement mémorable.
En 1901, il fit des observations astronomiques similaires à Stonehenge et examina avec beaucoup de soin ce monument et d’autres anciens monuments britanniques en pierre qui ont un caractère astronomique. L’alignement de l’axe de Stonehenge par rapport au point du lever du soleil au milieu de l’été, tel que montré par Sir Norman Lockyer, coïncidait non seulement avec la ligne centrale de l'"Avenue » (qui sera décrite plus tard), mais aussi avec la ligne joignant deux marques d’observation éloignées à l’horizon, aux extrémités opposées de la ligne de l’axe.
La première, dans le prolongement exact de la ligne centrale de l’avenue vers le point du lever du soleil au milieu de l’été, était une ancienne fortification britannique située au sommet de Sidbury Hill, à 8 miles de Stonehenge au nord-est. La seconde, vers le sud-ouest, ou le point du coucher du soleil au milieu de l’hiver, et également alignée avec l’axe du monument, produit dans cette direction, était marquée par la fortification de Grovely, à une distance de 6 miles de Stonehenge. Ces deux fortifications sont préhistoriques et les autorités archéologiques pensent qu’elles datent du début de l’âge du fer. Cette opinion a été exprimée par M. O.G.S. Crawford, officier d’archéologie du British Ordnance Survey, qui a étudié Stonehenge depuis les airs (voir « Article sur Stonehenge et Karnak », par A.R. Hinks, dans le XIX Century Magazine, juillet 1925, p. 127). Nous verrons, plus loin, la portée de cette affaire à la date de la construction de Stonehenge.
Le soin apporté à l’orientation de Stonehenge, et à la manière dont il était lié à ces marques d’observation lointaines à l’horizon, à la fois au point du lever du soleil au milieu de l’été au nord-est et au point du coucher du soleil au milieu de l’hiver au sud-ouest, suggère que cette ligne centrale indique la position solstitielle du soleil, à la fois au milieu de l’été et au milieu de l’hiver, à la date de la fondation du monument. La date astronomique, dérivée d’une courbe vraie de l’Obliquité de l’Écliptique pour les temps anciens, devrait donc s’accorder avec la date du monument trouvé par l’Archéologie, si cette dernière est également correctement établie.
Maintenant, il est très intéressant de noter que Sir Norman Lockyer, d’après ses observations astronomiques minutieuses en 1901, a trouvé que l’azimut moyen de la ligne d’axe de Stonehenge, aussi bien qu’il a pu le déterminer, était de 49° 35' 51" à l’est du nord. Ces observations ont été faites par Sir Norman en collaboration avec M. F.C. Penrose, un éminent archéologue et astronome, qui avait déjà fait une étude notable de l’orientation astronomique des anciens temples grecs.
Il dit ensuite que ce résultat « est confirmé par les informations également fournies par l’Ordnance Survey, à savoir qu’à partir du centre du Temple, le relèvement vers le nord-est de la marque principale sur une colline, à environ 8 milles de distance, la marque étant très proche d’un ancien campement britannique fortifié bien connu nommé Silbury ou Sidbury, est de 49° 34' 18" ; et que la même ligne continuait à travers Stonehenge, au sud-ouest, frappe une autre fortification ancienne, à savoir le château de Grovely, à environ 6 milles de distance. Pour les raisons ci-dessus, 49° 34' 18" a été adopté pour l’azimut de l’avenue.
Sir Norman poursuit en déterminant « quelle valeur devrait être donnée à la déclinaison du Soleil lorsqu’il apparaissait se montrant à 2' au-dessus de l’horizon, l’azimut étant de 49° 34' 18" ». Cette estimation de 2' (ou environ 1/15 du diamètre du soleil) comme marquant le point du lever du soleil visible est raisonnable, comme la plupart des gens notant le phénomène du lever du soleil seraient probablement d’accord.
La latitude de Stonehenge est de 51° 10' 42" N. ; et avec ces données et les autres données nécessaires, Sir Norman Lockyer a calculé que « la déclinaison du Soleil s’établit à 23° 54' 30 » N., et d’après les tables de l’obliquité de Stockwell, qui sont basées sur la détermination des éléments du système solaire, la date est 1680 av. J.-C. Sir Norman poursuit en disant qu'« en raison de la légère incertitude quant à la ligne d’observation originale, et du taux très lent de changement de l’obliquité de l’écliptique, la date ainsi dérivée est erronée de 200 ans plus ou moins ; cela nous donne une date de construction située entre, disons, 1900 et 1500 av. J.-C. Il adopta donc la date moyenne de 1700 av. J.-C. comme date probable de la fondation de Stonehenge.
Il fait ensuite remarquer qu'« une enquête archéologique indépendante effectuée, d’une manière des plus complètes et des plus admirables, juste après que M. Penrose et moi-même ayons obtenu notre conclusion, corrobore entièrement la date à laquelle nous étions arrivés ». Cette enquête archéologique a été menée au cours de l’été de la même année 1901 par le professeur Gowland, l’archéologue, qui a été chargé de diriger et d’examiner archéologiquement les fouilles nécessaires à la réérection de la célèbre « pierre penchée », qui était le montant occidental du grand trilithe central.
Le montant Eastern était encore couché sur le sol, brisé en deux morceaux, jusqu’au milieu de 1958, lorsqu’il a été remonté. Mais à la date où il est tombé, le compagnon debout de l’ouest a été laissé debout, mais en position penchée. Une fracture s’y était développée, et l’angle d’inclinaison avait augmenté, de sorte qu’on craignait qu’il ne tombe aussi. Par conséquent, sa réérection a été « recommandée à Sir Edmund Antrobus (le propriétaire de Stonehenge) par la Société des antiquaires de Londres et d’autres organismes savants, et cette réérection a été menée à son désir et à ses frais ». (voir Sir N. Lockyer, Stonehenge, édition de 1909, p. 69.)
Le professeur Gowland étudia à fond le grand nombre de spécimens archéologiques qu’il trouva, à savoir des instruments en silex, composés de haches de pierre, de pierres marteaux, de haches de marteau, de maillets pesant de 40 à 64 livres, ainsi que de grandes quantités de copeaux de Sarsen et de pierres bleues. Il est arrivé à la conclusion, pour ces raisons et d’autres, que Stonehenge a été construit vers la fin du néolithique, ou le début de l’âge du bronze en Grande-Bretagne, et il a finalement déclaré
À mon avis, la date à laquelle le cuivre ou le bronze a été connu pour la première fois en Grande-Bretagne est très éloignée... le début de leur application à des usages pratiques devrait, je pense, être placé au moins aussi loin que 1800 av. J.-C., et je suis enclin à donner cette date, jusqu’à ce que d’autres preuves soient apportées, comme la date approximative de l’érection de Stonehenge.
Il convient de mentionner ici que la formule de Newcomb pour l’obliquité a été adoptée plus tard par les astronomes comme la formule internationale standard. Si Sir Norman Lockyer l’avait eu à sa disposition à ce moment-là, il aurait trouvé, au lieu de 1680 av. J.-C., une date étonnamment plus proche de la date archéologique du professeur Gowland, à savoir 1822 av. J.-C. En fait, la bonne concordance entre les dates trouvées par Sir Norman Lockyer et le professeur Gowland fut d’abord accueillie avec beaucoup de satisfaction par les archéologues qui croyaient à la date très ancienne de Stonehenge.
Néanmoins, les travaux archéologiques approfondis qui ont été menés à Stonehenge ces derniers temps ont clairement montré que, bien qu’il y ait eu un cercle de pierres bleues antérieur à Stonehenge, remontant à l’âge du bronze, probablement vers 1800 av. J.-C., le grand cercle de Sarsen, beaucoup plus tardif, était une grande reconstruction, remplaçant le précédent, mais incorporant ses pierres bleues dans un nouveau design plus grand. à une époque qui n’est pas très antérieure à la période romano-britannique, qui a commencé au 1er siècle av. J.-C., et il est probablement prudent de l’attribuer à l’époque ancienne des druides, disons entre 300 et 400 av. J.-C., lorsque les druides étaient à l’apogée de leur puissance et de leur influence en Grande-Bretagne.
Sir Norman Lockyer a été impressionné par les preuves de cette reconstruction, bien que, comme nous le voyons maintenant, sa date astronomique, tout comme celle archéologique du professeur Gowland, soit beaucoup trop éloignée. Il dit (p. 95) : « La théorie à laquelle mon travail et ma pensée m’ont conduit est que les structures mégalithiques de Stonehenge – les sarsens travaillés avec leurs mortaises et leurs linteaux, et surtout les trilithes du magnifique naos – représentent une re-dédicace et une reconstruction, sur un plan et une échelle plus imposants, d’un temple beaucoup plus ancien. qui était à l’origine utilisé pour le culte en relation avec l’année de mai.
Les études archéologiques les plus récentes donnent une explication satisfaisante de l’utilisation à Stonehenge de haches, de marteaux et de maillets en pierre à l’ancienne pendant cette période, comme nous le verrons.
En ce qui concerne la divergence surprenante entre 1300 et 1400 ans dans la date astronomique de Stonehenge trouvée par Sir Norman Lockyer, nous verrons aussi que, comme dans le cas du Temple Solaire d’Amen Ra à Karnak, l’explication est contenue dans la ventilation complète des formules de Newcomb et de Stockwell, par elles-mêmes seules. pour donner la vraie place du Soleil dans les temps anciens. D’autre part, il faut prendre en considération le fait que la nouvelle Courbe de l’Obliquité ne fournit pas cette lacune qui, ajoutée à ces formules standards, leur permet de répondre à toutes les exigences de l’histoire et de l’archéologie. Il y a aussi beaucoup d’autres conséquences de grande portée que cela implique.
Afin d’y voir plus clair dans le cas de Stonehenge, considérons maintenant de la manière la plus complète possible, tout d’abord, une description générale du monument, puis les preuves archéologiques de la date de sa construction, et, enfin, l’astronomie de Stonehenge. Une partie de cela peut peut-être être quelque peu fastidieuse pour le lecteur général, mais pour ceux qui souhaitent examiner de près la question, il est nécessaire de donner les informations disponibles de manière très détaillée, comme suit.
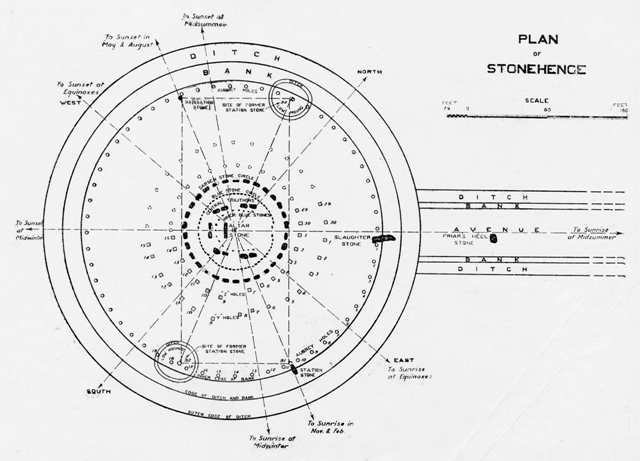
DESCRIPTION GÉNÉRALE DU MONUMENT
Les principales caractéristiques de Stonehenge sont
-
Le grand cercle des pierres de Sarsen
-
La formation en fer à cheval des Trilithes centraux
-
La formation intérieure en fer à cheval de pierres bleues
-
Le cercle de pierres bleues, entourant les formations en fer à cheval
-
La pierre de l’autel
-
les « Quatre Stations »
-
Les trous en Z et en V
-
Les trous d’Aubrey
-
La rive et le fossé environnants
-
L’Avenue, avec la pierre dite de l’abattage, et la « pierre du talon du frère ».
Afin de comprendre les résultats des recherches archéologiques et l’astronomie de Stonehenge, nous devons examiner en détail ces principales caractéristiques du monument.

http://crystalhatchlings.com/EasterEggs/Images/Stonehenge.jpg
Le grand cercle des pierres de Sarsen
Il s’agit de 30 immenses pierres verticales d’une moyenne de 18 pieds de haut en bas, d’une largeur de 7 pieds et d’une épaisseur de 3 pieds 9 pouces. Leur poids moyen est d’environ 26 tonnes chacun. On les laisse pénétrer dans le sol à une profondeur d’environ 4 ou 5 pieds, ou même plus, de manière à amener le sommet de chaque pierre exactement à la même hauteur, à 13 1/2 pieds au-dessus du sol. Ils sont disposés avec leurs bords intérieurs droit sur un cercle de 97 1/3 pieds de diamètre, selon les mesures faites par feu Sir Flinders Petrie.
Ces grandes pierres de Sarsen proviennent toutes du Wiltshire. Ils n’ont probablement pas été trouvés à Stonehenge, mais le site le plus proche, où il est probable qu’ils ont été exhumés et coupés presque en forme, était dans le North Wiltshire, à environ 16 à 20 miles de Stonehenge.
Le nom « Sarsen » appliqué à ces pierres, proviendrait de l’ancien nom saxon de « Saracen » (anglo-saxon « Saresyn »), d’un mot arabe signifiant oriental ou oriental, et se référant à un arabe ou musulman, impliquant aux premiers Saxons l’idée de païen ou païen. Les pierres « Sarsen » étaient de gros blocs de pierres, « rassemblés dans des temples, populairement attribués au culte païen ».
Ces pierres sont composées de grès, formé par le ciment naturel de sable et de gravier recouvrant la craie de cette partie du Wiltshire. Les blocs de pierres de Stonehenge sont très durs, si durs, en effet, que les ciseaux métalliques, à l’exception de l’acier le plus dur, seraient inutiles pour les travailler. Les constructeurs les travaillaient à coups écrasants avec des masses de pierre de quartzite pesant 50 livres ou plus, et aussi avec de petits marteaux de silex ou de quartzite pour couper les petites irrégularités.
Les espaces entre les pierres individuelles sont en moyenne de 3 1/2 pieds. D’après le plan et les mesures très précis de sir Flinders Petrie, la distance moyenne entre le centre d’une pierre et celui de la suivante était de 10 pieds 2 pouces.
Les constructeurs ont évidemment divisé le cercle en 30 parties égales, et ont érigé chaque pierre avec son centre sur le point ainsi déterminé. Les légères différences de largeur des pierres étaient compensées par des différences correspondantes dans la largeur des espaces entre elles.
Les pierres n°1 et n°30, de chaque côté de l’entrée sur la partie nord-est du monument sont une exception. Ils sont espacés de 6 pouces (l’espace d’entrée réel étant de 4 pieds de large), et la différence a été ajustée en réduisant les espaces voisins de chaque côté.
Ces montants étaient tous surmontés d’une couronne continue de grandes pierres de linteau, les extrémités adjacentes de deux linteaux reposant sur chaque montant. Ces pierres de linteau mesuraient en moyenne 10 1/2 pieds de longueur, 3 1/2 pieds de largeur et 2 pieds 8 pouces d’épaisseur. Ils pesaient un peu moins de 7 tonnes chacun. Selon le guide officiel de Stonehenge, la face intérieure des pierres de linteau a été soigneusement habillée à la courbe de la circonférence du cercle à laquelle la face intérieure des montants était tangente. D’autres descriptions indiquent que la face extérieure des pierres de linteau était également taillée à peu près à l’arc de son cercle.
Une caractéristique architecturale importante, montrant une grande amélioration par rapport à la conception des monuments en pierre britanniques antérieurs, est la manière dont les pierres de linteau étaient attachées aux montants. Le haut de chaque montant était travaillé de manière à laisser deux saillies coniques, ou tenons, une près de chaque extrémité. Sur la face intérieure de chaque linteau, une douille ou un trou de mortaise correspondant a été meulé, de manière à s’adapter précisément aux saillies. Les extrémités de chaque linteau étaient également coupées avec des « joints à bascule », une extrémité avec une rainure et l’autre avec une saillie. La saillie de chaque pierre de linteau s’insérait alors exactement dans la rainure de la pierre de linteau suivante de la série. Les saillies étaient triangulaires et s’étendaient verticalement du haut vers le bas de la pierre, et les rainures dans lesquelles elles s’inséraient étaient également triangulaires, formant une profonde encoche verticalement de haut en bas à l’autre extrémité de la pierre de linteau.
De plus, le haut des montants a été coupé avec des bords relevés comme un plateau peu profond, et correspondant à ceux-ci, les pierres de linteau ont été encastrées sur les bords pour s’adapter étroitement et solidement sur le dessus des montants.
Le colonel Hawley, qui a examiné ces points de près lorsque les linteaux au-dessus de la pierre d’entrée n° 1 ont été remis en place, a constaté que les joints à bascule s’adaptaient si bien qu’il était difficile de remettre les linteaux à leur place initiale.

http://media-2.web.britannica.com/eb-media/67/123467-004-EB688685.jpg
Les pierres verticales étaient faites pour s’effiler légèrement vers le haut, et cette conicité était généralement accompagnée d’un « entasis », ou léger gonflement de la tige de la colonne, un raffinement architectural qui jette de la lumière sur le travail avancé des constructeurs.
Lors de l’érection des montants, des trous de taille suffisante ont été creusés pour permettre l’ajustement de la pierre dans sa position exacte. Il était ensuite sécurisé par des blocs d’emballage. Certains d’entre eux sont connus pour provenir de Chilmark, à environ 13 miles de Stonehenge. Les trous étaient également pourvus, dans tous les cas sauf deux, d’une pente, ou rampe, le long de laquelle la pierre était glissée.
Au fond de chaque trou examiné se trouvait une rangée de trous, parfois de six pouces de diamètre, suggérant l’utilisation temporaire de poteaux en bois pour stabiliser le montant ou pour aider à l’ajuster à la bonne position.
Un fait important et remarquable, selon la déclaration officielle, est que du bois pourri y a été trouvé. Comme c’est le cas après une si longue période, entre 2000 et 3000 ans, cela indique que la décomposition bactérienne du bois a été excessivement lente.
Formation en fer à cheval des trilithes
À l’intérieur du grand cercle de pierres de Sarsen, et symétriquement placés autour du centre, se trouvent cinq grands trilithes de pierre de Sarsen, disposés en forme de fer à cheval. La longueur de cette formation en fer à cheval le long de la ligne axiale est de 44 pieds, et sa largeur à l’entrée ouverte et vers l’entrée nord-est du monument est également de 44 pieds.

http://www.timstouse.com/images/EarthHistory/Stonehenge11.jpg
Les montants de ces trilithes sont tous beaucoup plus hauts que ceux du cercle extérieur de Sarsen. Le central est le plus grand et est connu sous le nom de « Le Grand Trilithe » ou « Le Trilithe Central ». L’un de ses montants a 30 pieds de long et pèse 50 tonnes, et l’autre a 25 pieds de long.
Des trous ont été faits pour ceux-ci, suffisamment profonds pour permettre à la paire de se tenir à 22 pieds au-dessus du niveau actuel du sol. Avec sa grande pierre de linteau, le trilithe central s’élève à une hauteur totale de 25 1/2 pieds au-dessus du sol. Le plus court des deux montants avait un bossage de pierre non taillée à la base pour ajouter à sa stabilité.
Dans leur position d’origine, il y avait un espace d’exactement 3 pieds entre les montants du trilithe central, du niveau du sol à environ 4 1/2 pieds du sommet. On montrera que c’est exact plus tard, dans la discussion de l’axe du monument, et on verra que c’est important pour déterminer correctement la position de l’axe.
Il est également d’une importance particulière en ce qui concerne le dispositif de visée simple et unique utilisé par les anciens astronomes pour observer le point exact à l’horizon et pour vérifier la date du lever du soleil solstitiel du milieu de l’été à Stonehenge. Ceci est décrit plus loin dans la discussion sur l’astronomie de Stonehenge.
Les quatre autres trilithes sont regroupés en deux paires. La hauteur des montants de la paire adjacente au Trilithe central est de 17 pieds 9 pouces au-dessus du sol ; ou, en ajoutant la hauteur des linteaux, ces deux trilithes ont chacun 21 pieds 3 pouces de haut.
La paire de trilithes la plus extérieure a des montants de 16 1/2 pieds de haut, et en ajoutant les linteaux, leur hauteur totale au-dessus du sol est de 20 pieds.
La largeur des montants des cinq trilithes était, en moyenne, de 7 1/2 pieds au niveau du sol, avec un cône au sommet, réduisant la largeur à 6 1/2 pieds. Leur épaisseur était de 4 pieds au sol, s’amincissant au sommet à 3 pieds.
À l’instar des pierres du Grand Cercle, tous ces montants étaient marqués par un traitement « entasis ». les pierres de linteau des trilithes ont une longueur moyenne de 16 pieds et ont 3 pieds 6 pouces d’épaisseur ; Leur largeur au sommet est de 4 pieds 6 pouces et est réduite à 4 pieds en dessous. Le sommet de chaque montant de tous les trilithes était pourvu, au milieu ou près du milieu de sa surface supérieure, d’une saillie conique, ou tenon, semblable à celles des pierres du cercle de Sarsen, mais plus longue. Des douilles ou des mortaises ont été excavées sur la face inférieure de chaque pierre de linteau, de sorte qu’elle s’adapte exactement à la saillie correspondante.
Le fer à cheval intérieur en pierres bleues
Dans cette formation, il y avait 19 pierres bleues, sélectionnées pour leur forme symétrique. Ils ont été taillés en une sorte d’obélisque avec des sommets plats. Les hauteurs au-dessus du sol variaient de six à huit pieds, les plus hautes vers le centre.
Leur largeur et leur épaisseur moyennes étaient d’environ 2 pieds.
La pierre bleue centrale, cependant, juste en face du Trilithe central, avait 3 pieds de large, correspondant juste à l’espace de 3 pieds entre les montants du Trilithe central.
Le but de cela était évidemment lié à l’arrangement du dispositif de visée pour l’observation du lever du soleil au milieu de l’été, mentionné précédemment, et décrit plus loin. Cette pierre bleue centrale se trouvait à une distance de 3 pieds 6 pouces devant le trilithe central. La distance de son centre par rapport au centre de chacune des pierres bleues adjacentes de chaque côté était de 6 pieds 4 pouces, mais les intervalles de centre à centre entre les autres pierres bleues de cette formation étaient de 5 pieds 4 pouces.
Onze de ces pierres se trouvaient sur un demi-cercle d’un rayon de 20 pieds à partir du centre de l’ensemble du monument, et les quatre autres de chaque côté continuaient en ligne droite. Il y avait une largeur de 36 pieds à l’ouverture extérieure ou à l’entrée de cette formation en fer à cheval de pierres bleues.
Le colonel Hawley, cependant, a trouvé des indices d’autres personnes, complétant apparemment une formation elliptique.
Les pierres bleues de la formation intérieure en fer à cheval, ainsi que du cercle de pierres bleues entourant les trilithes, sont toutes d’origine ignée et n’appartiennent pas au Wiltshire. Deux types différents de pierres bleues ont été utilisés, à savoir les dolérites (roche ignée compacte, quelque peu cristalline, de couleur bleu-vert à gris verdâtre), et les rhyolites (roche volcanique, une variété de lave, de caractère silex et de couleur gris foncé). Il a été établi avec certitude qu’ils provenaient des montagnes Prescelly du Pembrokeshire, dans le sud du Pays de Galles. La partie orientale des monts Prescelly est riche en vestiges mégalithiques, et de nombreux cercles de « pierre bleue » ont été identifiés dans cette région.
Il se trouve à 180 milles par la route de Stonehenge, et que les pierres aient été amenées dans le Wiltshire entièrement par voie terrestre, ou en partie par mer de Milford Haven à la rivière Severn, et de là par voie terrestre, le transport a dû être un problème redoutable, et les associations traditionnelles liées à ces pierres bleues ont dû plaire très fortement aux constructeurs de Stonehenge.
Selon les anciennes traditions, on croyait généralement que ces pierres possédaient des propriétés magiques et médicinales. Il est possible, cependant, que les constructeurs ultérieurs de la grande formation de pierre de Sarsen aient trouvé les pierres bleues déjà apportées dans le Wiltshire, et certains pensent à Stonehenge même à une date beaucoup plus ancienne, et les ont incorporées dans leur structure ultérieure.
Le cercle de pierres bleues entourant les formations en fer à cheval
Les pierres de ce cercle intérieur sont de taille inégale et sont imparfaitement alignées sur un cercle d’environ 78 pieds de diamètre. Ce sont des pierres plates, d’environ 9 ou 10 pieds de long, et elles sont enfoncées dans le sol d’environ 3 pieds. Leur largeur moyenne est d’environ 2 1/2 pieds.
Les pierres d’entrée sont bien placées à l’intérieur de la circonférence, au lieu d’être sur celle-ci, et sont à un large intervalle. D’un centre à l’autre, il y a 8 pieds 7 pouces.
Un grand nombre de ces pierres ont disparu à cause des déprédations au Moyen Âge. Il a été suggéré que dans l’une de ces déprédations, les fondations du Trilithe central ont été creusées, peut-être à la recherche d’un trésor enfoui espéré, conduisant ainsi à la chute du montant oriental et à l’inclinaison du montant occidental.
Les premiers écrivains sur Stonehenge pensaient qu’il n’y avait que 30 ou 40 pierres dans le cercle de pierres bleues, mais le colonel Hawley, qui a fouillé près de la moitié du cercle en 1920, a découvert partout que les pierres ne se trouvaient à l’origine qu’à environ 18 pouces de distance. Les trous dans lesquels ils se trouvaient étaient reliés par une tranchée continue, dans laquelle une partie d’un flacon en verre du XVIIe siècle a été trouvée, ce qui suggère que la tranchée avait été creusée pendant cette période pour faciliter l’enlèvement des pierres perdues.
Il a également trouvé la distance réelle de la base des trous au fond, et parfois il y avait des fragments brisés ou des souches des pierres restantes encore. D’après les preuves qu’il a trouvées, le colonel Hawley a estimé que le nombre de pierres dans ce cercle de pierres bleues était à l’origine d’environ 60.
Deux de ces pierres du cercle de pierres bleues ont été trouvées avec des creux en forme de coupe, comme des mortaises, comme si ces pierres avaient été destinées à être utilisées comme linteau, et la possibilité est ainsi indiquée qu’elles ont pu être des pierres de linteau dans un cercle existant auparavant, et ont été utilisées dans la conception reconstruite.
Les pierres du cercle de pierres bleues et celles de la formation intérieure en fer à cheval, mais plus particulièrement cette dernière, ont été travaillées et taillées pour prendre forme sur place à Stonehenge. Les pierres du cercle de pierres bleues sont rugueuses et irrégulières, et de formes diverses. Ils ne montrent des signes que d’une petite quantité de pansement et, en général, sont pratiquement des rochers non taillés.
D’autre part, les pierres bleues du fer à cheval intérieur ont été taillées et habillées de manière approfondie. Dans les trous qui ont été creusés, la quantité d’éclats de pierre bleue était beaucoup plus importante que celle des pierres de Sarsen. On dit qu’elles ont été taillées et taillées d’une manière extraordinaire, et le professeur Judd a estimé qu’elles avaient été réduites à près de la moitié de leurs dimensions dans ce processus, les éclats étant presque égaux au volume des pierres elles-mêmes.
Le fait qu’ils aient été ainsi traités à Stonehenge, au lieu de l’endroit d’où ils avaient été initialement apportés, au cours d’un si long voyage de 180 miles, suggère que, selon les mots de Sir Normal Lockyer, ils et le grand monument de Sarsen "représentent une nouvelle dédicace et une reconstruction, sur un plan et une échelle plus imposants, d’un temple beaucoup plus ancien.
C’était peut-être soit à Stonehenge même, soit quelque part à proximité dans le Wiltshire. Ce problème sera examiné plus en détail dans le cadre des « trous Aubrey ».
Il s’agit d’une grande dalle plate de grès micacé, qui proviendrait de Milford Haven, dans le sud du Pays de Galles, où l’on trouve de la pierre de ce type. Il mesure 16 pieds de long, 3 pieds 4 pouces de large et 1 pied 9 pouces d’épaisseur. Il repose à plat sur le sol à l’intérieur de la formation intérieure en fer à cheval de pierres bleues, et presque symétriquement dans l’axe du monument.
On pense qu’il a probablement été placé dans une position vraiment symétrique et qu’il a été déplacé par la chute des grosses pierres du trilithe qui se trouvent maintenant au-dessus de lui (la moitié supérieure du montant oriental brisé et la pierre de linteau du trilithe central). Les preuves indiquent la probabilité qu’il ait été placé à l’origine dans une position plate, le centre étant à 14 pieds en avant du grand Trilithe central.
Ce nom a été donné à deux pierres de Sarsen, nos 91 et 93, et à deux monticules bas, nos 92 et 94, qui se trouvent juste à l’intérieur de la berge sur la circonférence du cercle de trous d’Aubrey, ou très près de celle-ci. Il a été montré que les deux monts sont les sites des pierres de Sarsen, comme 91 et 93, qui étaient placées à l’origine au centre des monts.
Ces quatre pierres avaient alors un caractère géométrique et astronomique remarquable. Dans le placez d’abord les lignes joignant les lignes 91 à 93, et 92 à 94, qui se coupent au centre de l’ensemble du Monument. De plus, les lignes joignant les bords intérieurs de 91 à 94 et de 92 à 93 sont tangentes à la circonférence extérieure du grand cercle de Sarsen.
Ainsi, en regardant de 91 à 94, ou de 92 à 93, ces pierres étaient complètement visibles les unes des autres, et elles forment un rectangle, symétrique avec l’axe du Monument, et entourent le Cercle de Sarsen. Cette disposition géométrique semble avoir été une caractéristique structurelle du plan de construction original, et peut avoir été obtenue comme suit :
La distance entre le bord extérieur du cercle du fossé et le centre du cercle de Sarsen est de 184 1/2 pieds (d’après les mesures de sir Flinders Petrie). Avec le centre D, sur le bord extérieur du cercle du fossé, et sur la ligne d’axe, un cercle est tracé avec un rayon D1C1 = 184,5 pieds.
D1S1 et D1S4 sont deux rayons de ce cercle, perpendiculaires l’un à l’autre, avec l’angle droit S1D1S4 coupé en deux par l’axe D1C1D2.
alors D1S1 = D1S4 = D1C1 = 184,5 pieds
et D1E = ES1 = ES4 = 130,5 pieds
où E est le point de bissection de S1S4 par le axe ligne D1C1D2et S1S4 sont les emplacements des pierres de la station 91, 94
et la distance entre leurs centres S1S4 = 261 pieds.
Avec le centre C1, trois cercles sont tracés avec des rayons
C1G = 48,5 pieds = rayon du bord intérieur du cercle de Sarsen C
1F = 52,5 pieds = rayon du bord extérieur du cercle de Sarsen C
1E = 54,0 pieds = rayon du bord extérieur du cercle de Sarsen plus de la moitié de l’épaisseur des pierres de station 91, 94.
Alors S1S4 est une tangente au cercle extérieur en E et la droite joignant les bords intérieurs des pierres de la station 91, 94, est une tangente à la circonférence extérieure du cercle de Sarsen en F.
Un rectangle S1S2S3S4 est ensuite construit, dont S2S3 sont les sites des pierres de la station 92, 93.
S1S2 = S3S4 = 108 pieds = diamètre du cercle
extérieur S2S3 = S1S4 = 261 pieds
De plus, S2S3 est une tangente au cercle extérieur en J, et la ligne joignant les bords intérieurs des pierres de station 92, 93, est une tangente à la circonférence extérieure du cercle de Sarsen en I.
De plus, les diagonales S1S3 et S2S4 se coupent au centre du cercle de Sarsen avec des angles de 45°, à savoir S1C1S2 et S3C1S4, au point d’intersection. C’est une conséquence nécessaire de la construction.
Les mesures ci-dessus sont celles du monument, en accord substantiel avec les mesures effectuées par Sir Flinders Petrie, et la figure géométrique a fourni un moyen simple et efficace de planifier la construction du cercle de Stonehenge de manière symétrique et précise.
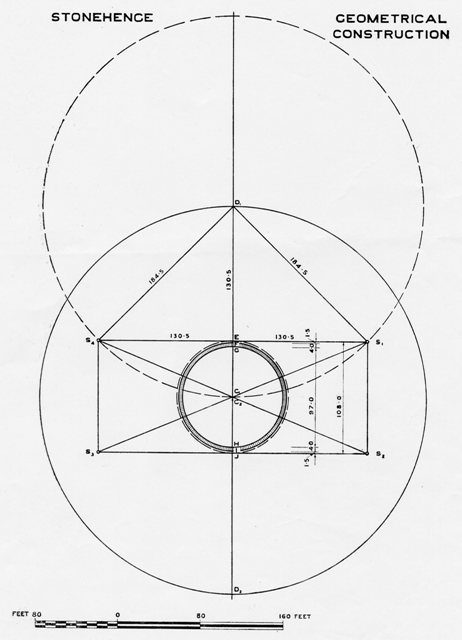
En outre, il convient de souligner que si les détails de cette figure géométrique étaient mesurés au sol, cela fournirait un moyen simple de vérifier l’exactitude de l’axe indiqué ci-après.
La question se pose maintenant : pourquoi le centre du cercle du fossé n’a-t-il pas été adopté comme centre du cercle de Sarsen ? Le centre du cercle du fossé est le même que celui du cercle d’Aubrey, mais il se trouve à 2 3/4 pieds au sud du centre du cercle de Sarsen, selon les mesures faites par Sir Flinders Petrie.
On aurait pu employer la même construction géométrique, et les diagonales du plus grand rectangle ainsi obtenu auraient encore fait un angle de 45° l’une avec l’autre au centre, mais le cercle de Sarsen aurait été un peu plus grand, et son diamètre aurait été plus grand que celui adopté, qui était de 97 pieds.
Peut-être l’explication est-elle liée à ce fait, car, selon la suggestion de Sir Flinders Petrie, le diamètre intérieur du cercle de Stonehenge, environ 97 pieds, ou 1164 pouces, est dérivé de l’Égypte, où il apparaît généralement comme 1162 ou 1164 pouces britanniques. C’est le diamètre d’un cercle dont la circonférence est dix fois le nombre de jours d’une année solaire, dans les unités de mesure adoptées.
Le cercle de l’année standard était la base non seulement du système de mesures égyptien, mais aussi de l’ancienne mesure circulaire chinoise, dans laquelle le cercle standard était divisé en 365 1/4 degrés, pour correspondre au nombre de jours dans une année solaire.
On dit que le pouce standard de l’Égypte ancienne est égal à 1,0011 pouce britannique moderne.
Le diamètre du cercle de Stonehenge, environ 1164 pouces britanniques, serait alors égal à 1162,7 pouces égyptiens primitifs. S’il était plus petit de 1/10 de pouce, c’est-à-dire 1162,6 pouces, alors la circonférence du cercle serait exactement de 3652,42 pouces, c’est-à-dire la valeur de l’Égypte ancienne pour dix fois le nombre de jours de l’année solaire.
Le diamètre intérieur du cercle de Stonehenge est généralement donné à 97 1/3 pieds, d’après les mesures de Sir Flinders Petrie ; mais, compte tenu de la difficulté de la mesurer exactement, il semble évident que Sir Flinders Petrie considérait que l’étroite coïncidence avec l’ancien cercle de l’année et du jour rend probable que les constructeurs avaient l’intention de faire de Stonehenge aussi proche que possible de cette taille particulière, en accord avec le caractère astronomique unique de la structure.
Les monticules des « Quatre Stations » ont environ 40 pieds de diamètre. Chacune était entourée d’un fossé circulaire. Chaque monticule couvre le site d’au moins deux trous d’Aubrey, et le colonel Hawley, en explorant le trou sud (n° 92), a découvert que le fossé coupe le trou d’Aubrey n° 19, et que la zone entourée par le fossé était recouverte d’un sol plat de craie et d’argile mélangées durement battues.
Lors de l’inhumation d’os brûlés, on a trouvé dans le monticule nord (n° 94), mais cela s’explique par la crémation habituelle associée aux trous d’Aubrey.
En ce qui concerne la signification astronomique des « quatre stations », les lignes reliant 91 (est-sud-est) à 92 (sud-sud-est) et 93 (ouest-nord-ouest) à 94 (nord-nord-ouest) sont parallèles à l’axe du monument. Ils indiquent le lever du soleil au milieu de l’été dans une direction, au nord-est, et le coucher du soleil au milieu de l’hiver dans la direction opposée, au sud-ouest. De plus, la ligne diagonale joignant 93 à 91 indique la position où le soleil s’est levé, dans l’Antiquité, le 8 novembre et le 4 février.
En regardant dans la direction opposée, de 91 à 93, la ligne indique le coucher du soleil le 6 mai et le 8 août. Ces quatre dates étaient « les quatre grandes fêtes des druides » et représentaient des tournants importants dans les saisons.
Cependant, ces pierres ne sont pas visibles les unes des autres, car la ligne de vue est bloquée par les grandes pierres du cercle de Sarsen. S’ils avaient été utilisés à des fins d’observation, il semble probable que l’observateur aurait dû se tenir à l’extérieur du cercle de Sarsen, devant la pierre de Sarsen n° 6 et, regardant vers la pierre de la station 91, il aurait pu l’utiliser à des fins d’observation sur un point reconnu de l’horizon où le soleil s’est levé le 8 novembre et le 4 février ou d’autres positions proches de celui-ci lorsque le soleil s’est approché de ce point. avant ces jours de saison et de festival.
De même, debout à l’extérieur du cercle de Sarsen, et devant la pierre 21 de Sarsen, il pouvait regarder vers la station 93 pour observer la position du coucher du soleil pendant et avant les jours de saison tout aussi importants, le 6 mai et le 8 août.
Beaucoup d’informations intéressantes concernant l’ancienne division de l’année celtique, ainsi que les fêtes et les coutumes qui s’y rattachent, sont données par le Dr J.A. MacCulloch dans Religion of the Ancient Celts, 1911, p 256 etc ; aussi par T.D. Kendrick dans The Druids, 1928, pp 115-120 et 129-130 ; et par G.H. Bonner dans un article sur les druides, dans la revue « Nineteenth Century », septembre 1925, pp. 422-430.
Ces écrivains ont fait remarquer qu’à une époque reculée, l’année celtique était une année lunaire. Mais il existe des preuves qu’une année solaire a été utilisée plus tard. C’était, en fait, nécessaire à des fins pastorales et agricoles.
Dans leur calendrier solaire précoce, l’année celtique commençait le 8 novembre, lorsque le temps chaud de l’été et de l’automne cessait et que la moitié froide ou hivernale de l’année commençait. L’opportunité de commencer l’année tôt en novembre était sans aucun doute liée à la nécessité de mettre les moutons et le bétail à l’abri à ce moment-là, et de les nourrir avec de la nourriture stockée pendant la partie hivernale rigoureuse de l’année, pendant environ six semaines avant et après le solstice d’hiver. Ce début de mois de novembre était lié à l’année astronomique solaire en se situant à mi-chemin entre l’équinoxe de septembre (automne) et le solstice de décembre (milieu de l’hiver).
La moitié froide de l’année dura jusqu’au 6 mai, date à laquelle, une fois terminée, la moitié chaude ou estivale de l’année commença.
Au milieu de la moitié froide, le 4 février, selon les calculs astronomiques, la période du milieu de l’hiver était terminée et le printemps était considéré comme commençant. C’était la date intermédiaire entre le solstice de décembre (milieu de l’hiver) et l’équinoxe de mars (printemps). De même, le 6 mai, ou le début de la moitié chaude de l’année, était à mi-chemin entre l’équinoxe de mars et le solstice de juin (milieu de l’été).
De la même manière, la date intermédiaire entre le solstice de juin et l’équinoxe de septembre (d’automne), à savoir le 8 août, était considérée astronomiquement comme marquant le début de l’automne. L’automne se termina, en même temps que la fin de la moitié chaude de l’année, et l’hiver recommença, avec le commencement du Nouvel An suivant, le 8 novembre.
Afin de marquer ces dates importantes, ainsi que les dates des solstices et des équinoxes, il était nécessaire pour ceux qui étaient responsables du calendrier de construire des structures astronomiques permanentes telles que Stonehenge et toute autre pierre, ou même une structure en poteaux de bois, comme Woodhenge, dans de nombreuses parties des îles britanniques, et ailleurs en Europe. afin d’observer la position du soleil sur l’horizon à ses points de lever et de coucher à toutes les périodes importantes du mouvement annuel du soleil.
L’application et l’importance de tous les alignements astronomiques du grand cercle de Stonehenge et de ses « quatre stations » peuvent ainsi être facilement reconnues.
De plus, si l’axe de Stonehenge peut être déterminé avec certitude, et si l’astronomie de Stonehenge est correctement établie, il doit alors nécessairement être possible par des moyens astronomiques de déterminer la date approximative de sa construction, en accord avec les preuves archéologiques exactes et avec les preuves historiques, si elles sont disponibles.
En ce qui concerne le calendrier en usage à l’époque de la construction de Stonehenge, on peut considérer comme certain que les dates astronomiques, mentionnées ci-dessus, facilement vérifiables par l’observation d’une année à l’autre, ont été utilisées ; Des feux de joie étaient allumés les soirs précédant les jours indiquant les changements de saisons, et des fêtes étaient célébrées aux jours ainsi fixés.
De plus, l’observation du lever du soleil solstitiel le jour du milieu de l’été était la caractéristique principale du Stonehenge, et le jour du milieu de l’été était marqué par un festival spécial dès les temps les plus anciens.
Le coucher de soleil du milieu de l’hiver, sur le château de Grovely, coïncidant avec le prolongement de l’axe de Stonehenge vers le sud-ouest, aurait également pu être observé dans des conditions météorologiques favorables, mais sans doute en raison de cette difficulté, on y attachait beaucoup moins d’importance. Cependant, la combustion traditionnelle moderne de la bûche de Noël indique la survie de la coutume séculaire d’allumer le feu pour se réjouir de l’arrivée anticipée de jours plus longs et plus chauds après le solstice d’hiver.
Les équinoxes, eux aussi, auraient facilement pu être observés depuis une construction astronomique aussi unique que Stonehenge. Mais ces périodes, bien qu’importantes sur le plan astronomique, n’étaient pas marquées par des fêtes populaires dans l’Antiquité celtique.
Bien que les dates astronomiques des tournants saisonniers de novembre, février, mai et août aient été tout à fait précises, le Dr MacCulloch note néanmoins que Beltane et Samhain, les fêtes qui marquaient le début de la moitié chaude de l’année au début de mai et le début de la moitié froide au début de novembre, respectivement, "étaient peut-être d’abord des fêtes mobiles, selon que les signes de l’été ou de l’hiver sont apparus plus tôt ou plus tard. Avec l’adoption du calendrier romain, certaines fêtes ont été déplacées...
Dans le système celtique, tel qu’il est donné par le Dr MacCulloch et tiré des textes irlandais, la division de l’année était la suivante :
Geimredh (moitié d’hiver)
- Premier trimestre – Geimredh, à partir de la fête de Samhain, le 1er novembre.
- Deuxième trimestre – Earrach, à partir du 1er février (parfois appelé Oimelc)
Samhradh (Moitié d’été)
On remarquera que dans ce calendrier, les dates astronomiques antérieures de novembre, février, mai et août ont été reportées au 1er du mois dans chaque cas.
Sir Norman Lockyer, dans son livre sur Stonehenge (p. 181), dit à propos de ces dates astronomiques, qu’il n’y a aucun doute qu’à ces dates ou aux alentours de ces dates « les fêtes étaient autrefois célébrées dans ces îles ».
Même au Xe siècle, Cormac, archevêque de Cashel, en Irlande, aurait dit que « de son temps, il y avait quatre grandes fêtes des druides, à savoir en février, mai, août et novembre ».
On ne sait pas avec certitude combien de temps les dattes druidiques ont été utilisées pour les fêtes en Angleterre, mais dans toute la Grande-Bretagne, elles ont été progressivement déplacées vers le système ultérieur de dates à la suite de l’introduction du christianisme en Grande-Bretagne.
Les anciennes fêtes ne tenaient pas compte des jours de la semaine, de sorte qu’il fut décidé que les fêtes devaient avoir lieu le premier jour de la semaine ; Plus tard, il fut décidé que certains d’entre eux commençaient le premier jour du mois.
Au début, il y avait une Pâques fixe, le 22 mars, et la fête de février s’est transformée en mercredi des Cendres, le 4 février, lorsque les cendres des feux de joie de la nuit précédente (mardi gras) ont été utilisées en relation avec les coutumes du Carême précoce. Avec l’adoption d’une Pâques mobile, une certaine confusion s’est produite dans la fixation des dates des fêtes, mais il semble qu’il y ait eu une tendance naturelle à adopter le premier du mois pour les quatre fêtes saisonnières de novembre, février, mai et août.
La fête de l’église « All Hallows », ou « Hallowmass », a été instituée vers 610 après JC en mémoire des martyrs, et a pris la place de l’ancienne fête saisonnière le 1er mai. Cela a été changé en 834 après JC et la fête a été fixée au 1er novembre et a reçu le nom de Toussaint, en commémoration de tous les saints, tandis que la fête de toutes les âmes, auparavant une commémoration des morts le 1er novembre, a été généralement transférée au 2 novembre.
Un autre changement qui s’est opéré dans l’ancien système celtique a été le transfert du début de l’année de début novembre au 25 mars, quelques jours après l’équinoxe de printemps. Cette date est devenue la date officielle du début de l’année en Angleterre jusqu’en 1752, date à laquelle le calendrier grégorien a été adopté en Angleterre.
La même année, en septembre 1752, il fut décrété que le commencement de l’année serait le 1er janvier, date qui avait été choisie par Jules César en 45 av. J.-C., lorsqu’il avait rectifié le calendrier romain, et qui avait été acceptée par le pape Grégoire XIII comme le début de l’année lorsqu’il inaugura le calendrier grégorien en 1582 après J.-C.
Pour en revenir à l’examen de l’ancien calendrier celtique, conservé dans les alignements des pierres de Stonehenge, la veille de Samhain, le commencement de l’année, était célébrée par des feux de joie. Cette soirée a survécu en Écosse et dans certaines parties de l’Angleterre sous le nom d’Halloween, la veille de la Toussaint, le 1er novembre. Samhain était une fête au cours de laquelle tous les différends étaient réglés. Il y avait aussi une commémoration annuelle des morts, qui a survécu en Angleterre et dans d’autres pays sous le nom de All Death' Day.
Cette commémoration des morts était une fête très ancienne, maintenue au début du mois de novembre dans de nombreux pays, y compris l’Égypte ancienne, le Mexique, la Perse et même les aborigènes australiens disent que les Pléiades se lèvent en début de soirée de ce mois.
Au début de l’Égypte, le jour de l’An tombait le 1er novembre, et la commémoration des morts ce jour-là faisait référence à la traditionnelle « destruction de l’humanité » dans le déluge. Cela s’est passé, dans le récit de la Genèse, le 17e jour du deuxième mois.
Il a été suggéré (D. Davidson, The Great Pyramid, p. 31) que l’année civile de la Genèse était une année intercalaire de 360 jours (chacun des 12 mois d’une durée de 30 jours), influencée par rapport à l’équinoxe d’automne ; et que l’année du Déluge, elle commençait le 16 septembre (date grégorienne), et que le 17e jour du 2e mois correspondait au 1er novembre du calendrier égyptien primitif.
À l’époque celtique, les druides avaient des cérémonies spéciales ce jour-là. « L’une des plus importantes a été la réactivation du feu. Tous les feux privés étaient éteints lors de cette fête, et ne pouvaient être rallumés qu’à partir du feu sacré... Parmi les autres pratiques druidiques, il y avait celle de marcher autour de l’autel dans la direction du soleil... Les animaux étaient abattus et la nourriture stockée pour l’hiver.
Le 1er février, lors de la fête celtique irlandaise, Brighde, ou Brigit, était vénérée comme une déesse du feu ou de la rosée, et cette date est encore célébrée comme la fête irlandaise de la Sainte-Bride ou de la Sainte-Brigit, les feux de Brighde ayant fait place aux cierges de la Chandeleur. Au sanctuaire de Sainte-Brigit à Kildare, « un feu sacré qui ne doit pas être soufflé ou approché par un homme, était surveillé quotidiennement par 19 nonnes à tour de rôle ». (Religion des anciens Celtes, p. 69)
La veille du 1er mai, veille de mai ou Beltane, était un moment de réjouissance devant le retour du soleil. Ces fêtes et les autres étaient observées dans toute la France, l’Angleterre, le Pays de Galles, l’Écosse et l’Irlande et, à la fin de l’époque celtique, elles étaient associées aux druides, qui effectuaient des rites spéciaux à ces occasions. Il est dit qu’à Beltane, les druides avaient l’habitude de faire deux feux, en les accompagnant d’incantations, et en conduisant le bétail entre les feux pour se prémunir contre les maladies ; tandis qu’en Écosse, jusqu’au XVIIIe siècle, les feux de Beltane étaient allumés sur un monticule artificiel entouré d’un mur circulaire bas et surmonté d’une pierre verticale, traditionnellement un lieu de culte druidique, puis un lieu de tenue de cours de justice.
Dans de nombreuses régions d’Angleterre, le 1er mai est encore observé, en particulier par les enfants, et une ancienne coutume survit au Magdalen College d’Oxford, où, le matin de mai, la chorale chante un chant latin au lever du soleil au sommet de la tour.
Le jour de la Saint-Jean, le 21 juin, était célébré à l’époque celtique d’une manière semblable à celle de Beltane. Les feux de joie de la veille de la Saint-Jean, précédant le jour de la fête, étaient une partie centrale des procédures, avec des danses et des chants, des sauts à travers le feu, y conduisant le bétail pour éloigner les maladies, et dans les temps très anciens, comme mentionné par Jules César et d’autres écrivains anciens, des victimes humaines et des animaux étaient sacrifiés.
Un arbre occupait une place de choix dans les fêtes de Beltane et de la Saint-Jean, et était porté en procession ; et, comme pour l’arbre de Noël jusqu’à nos jours, des branches de celui-ci étaient attachées aux maisons. De plus, une roue enflammée, représentant le soleil, a été roulée en bas d’une colline, ou à travers les champs, ou des marques enflammées ont été tournoyées.
À l’époque chrétienne, la fête du milieu de l’été, le jour même du solstice, était remplacée par la fête de l’église de Saint-Jean-Baptiste, célébrée maintenant le 24 juin, chaque année. À cette occasion, un sermon est prêché chaque année dans le quadrilatère du Magdalen College d’Oxford pendant la journée, comme une coutume séculaire, pour marquer la journée.
Le 1er août, qui a pris la place de la date saisonnière antérieure, le 8 août, à mi-chemin entre Beltane (6 mai) et le Samhain suivant (8 novembre) était le jour où l’automne était considéré comme le commencement. Il était appelé Lugnasad par les Celtes irlandais et était une fête importante dans toute la Grande-Bretagne, ainsi qu’en Europe, étant la fête de la moisson. À l’époque romaine, on l’appelait la « fête d’Auguste » et plus tard la « fête d’août ». Avec l’essor du christianisme, il a été remplacé par le « Jour de Lammas ».
Selon certains auteurs, ce nom est dérivé du gaélique La Mas Ubhal, le jour de la pomme ; mais la dérivation la plus généralement acceptée est celle de l’anglo-saxon Hlaf-maesse, pain-masse, ou fête d’action de grâces pour la moisson. Il est encore marqué par des festivités ou des foires dans certaines parties du pays et, comme le dit le Dr MacCulloch (p. 272 de son livre), « autrefois des assemblées dans des centres commodes se tenaient ce jour-là, non seulement à des fins religieuses, mais aussi pour le commerce et le plaisir ».
Le 1er août, ou plutôt le lundi suivant cette date, est toujours observé en Angleterre comme un « jour férié » national, maintenant ainsi la continuité avec l’ancienne fête d’automne.
Les équinoxes, en mars et septembre, n’étaient pas marqués dans les temps celtiques anciens, par d’importantes fêtes populaires dans la même mesure que les autres dates saisonnières, mentionnées ci-dessus.
Stonehenge était clairement bien adapté pour observer la position du soleil au lever et au coucher du soleil au moment des équinoxes, et ainsi vérifier les dates équinoxiales d’une année à l’autre. Néanmoins, ce n’est qu’avec l’introduction du christianisme, avec d’abord une Pâques fixée au 22 mars, qu’une grande fête publique s’est synchronisée étroitement avec l’équinoxe de printemps. Cependant, cette association étroite de Pâques avec la date de l’équinoxe a été brisée par la suite par l’adoption d’une Pâques mobile, après l’arrivée de saint Augustin en Angleterre en 597 après J.-C. En effet, le Vendredi saint et le dimanche de Pâques ont toujours été traditionnellement liés à la Pâque juive, dont la date était calculée, non pas par un calendrier solaire fixe, mais par la date du calendrier luni-solaire juif de la pleine lune pascale le 15e jour du mois lunaire juif Nisan.
De plus, il avait semblé souhaitable, et cela a été ordonné par le concile de Nice en 325 après J.-C., que les chrétiens de partout observeraient la fête du jour de Pâques à la même date, qui avait été spécifiée comme « le dimanche après la première pleine lune tombant sur ou après l’équinoxe de printemps », et cette année-là, l’équinoxe était considéré comme étant le 21 mars.
Une certaine confusion s’est produite au sujet de la date de Pâques au cours des années suivantes, en raison des défauts croissants du calendrier julien, mis en usage par Jules César en 46 av. J.-C. Le calendrier julien a été utilisé en Angleterre jusqu’en 1752, date à laquelle l’équinoxe de printemps était redescendu de onze jours par rapport à sa date julienne.
Après l’adoption du calendrier grégorien en Angleterre en 1752, de nouvelles tables ont été compilées pour calculer la date de Pâques ; et, conformément à ces tableaux, le dimanche de Pâques a un large éventail de dates, variant selon les années entre la date la plus ancienne, le 22 mars, et la date la plus tardive possible, le 25 avril, c’est-à-dire une plage de trente-cinq jours. La fête chrétienne de Pâques n’est donc pas saisonnière au sens où l’étaient celles de la période celtique. Son lien avec l’équinoxe de printemps est indirect et historique, remontant au premier Vendredi saint et au jour de Pâques, et de là à 1515 ans en arrière jusqu’à l’institution de la première Pâque à l’époque de Moïse et de l’Exode.
À cette époque, un nouveau commencement de l’année hébraïque était spécialement ordonné, avec son premier mois lunaire Abib ou Nisan, ayant sa pleine lune (la pleine lune pascale) le quinzième jour du mois, le ou immédiatement après le jour de l’équinoxe de printemps.
En ce qui concerne l’équinoxe d’automne (23 septembre), il n’y avait pas de fête celtique importante pour le célébrer, et la plus proche des fêtes chrétiennes ultérieures est celle de la Saint-Michel et de tous les anges (jour de la Saint-Michel) le 29 septembre, associée aux fêtes de la Saint-Michel à cette saison de l’année.
D’après le récit des quatre stations et de l’orientation estivale de Stonehenge, et des grandes fêtes celtiques aux dates correspondant aux différents alignements, nous pouvons clairement voir l’importance astronomique de cette structure unique, et le soin pris par les constructeurs pour assurer l’exactitude de ces alignements.
Ce sont des trous trouvés à l’extérieur du cercle de Sarsen, à la suite des investigations du colonel Hawley en 1920. Ils sont d’une importance particulière à cause de l’indice qu’ils donnent à la date à laquelle ils ont été creusés, et de là à la date du grand cercle de Sarsen.
Ils se composent d’environ 60 trous oblongs, d’environ 5 pieds de long et 3 pieds de profondeur. Au fond, ils sont réduits à 2 à 2 1/2 pieds de long et 1 1/2 à 2 pieds de large. Ils sont disposés grossièrement en deux cercles concentriques avec le cercle de Sarsen, le rayon du cercle Z étant de 65 pieds et celui du cercle Y de 90 pieds. Les trous Z et Y se trouvent directement derrière et à l’extérieur des montants du cercle Sarsen, les trous Z à une distance de 12 1/2 pieds et les trous Y à 37 1/2 pieds du bord extérieur des montants du cercle Sarsen.
Ils contiennent des éclats de pierre bleue sur le fond, et certains d’entre eux ont été découpés dans les rampes inclinées des trous de Sarsen, utilisés dans l’érection des montants de Sarsen. C’est important, car, comme le souligne le guide officiel de Stonehenge (p. 23), compilé par Frank Stevens (directeur du musée de Salisbury) et publié en 1938, il montre qu'« ils ont été creusés après l’érection des montants ». L’irrégularité de ces trous est un trait particulier, tout à fait en désaccord avec la précision de la plus grande partie du monument.
Le colonel Cunnington pense qu’elles ont peut-être été initialement destinées, bien qu’elles n’aient pas finalement été utilisées, pour les pierres du cercle de pierres bleues, en raison de la coïncidence apparente du nombre de ces pierres avec le nombre total de trous Z et Y, qui devrait être de 60 au total, bien que Z8 soit manquant et Y7 seulement partiellement creusé. Il y a cependant deux grands trous de poteau près de la position de Z8.
D’autre part, la possibilité a été suggérée qu’ils étaient « de construction » et « liés d’une manière ou d’une autre à l’élévation des pierres de linteau ». (voir guide officiel, p. 23) Cette suggestion semble probable. Auraient-ils pu être utilisés dans le processus d’érection des montants de Sarsen ?
Si les pierres bleues du cercle de pierres bleues formaient à l’origine le cercle d’Aubrey, comme leur nombre (environ 60, y compris deux pierres de linteau probables) le suggère, n’auraient-elles pas, après avoir été retirées de ce cercle, avoir été temporairement utilisées dans les trous Z et Y comme butées arrière, ou ancrages, pendant le processus d’érection des montants, ainsi que les linteaux du cercle de Sarsen ; et, une fois que tout a été terminé, enfin mis en position dans le Cercle de Pierre Bleue ?
Lorsque les montants Sarsen étaient mis en position et basculés dans les trous préparés pour eux, ils reposaient en partie sur les rampes menant aux trous, et ils se projetaient vers l’arrière à un faible angle sur une distance de 16 pieds ou plus. Dans cette position, des poteaux éventuellement robustes, basés sur des ancrages dans les trous en Y, et progressivement élevés au fur et à mesure que les grandes pierres de Sarsen étaient soulevées, constitueraient un support efficace, prévenant le danger que les Sarsen tombent en arrière par accident.
À un stade ultérieur, lorsque les pierres de Sarsen étaient inclinées à un angle plus raide, des entretoises plus courtes basées sur des ancrages dans les trous en Z pouvaient être utilisées jusqu’à ce que les pierres de Sarsen soient complètement érigées. De plus, pour élever les pierres de linteau du cercle de Sarsen, une méthode pratique d’utilisation des trous en Z et en Y aurait sans doute pu être utilisée, comme le suggère le guide officiel.
Si les trous Z et Y étaient utilisés à cette fin, cela expliquerait leur nombre et leur position dans l’alignement du milieu des pierres du cercle de Sarsen, ainsi que leur irrégularité, car il n’y aurait aucun avantage à leur donner une précision géométrique pour une utilisation temporaire dans la construction.
Le point très important à propos des trous Z et Y est la lumière qu’ils projettent à la date de construction du cercle de Sarsen. Car ils contiennent un grand nombre de morceaux de poterie brisés, qui appartiennent au début de l’âge du fer, ou périodes romano-britanniques, entre 500 av. J.-C. et 1 ap. J.-C.
D’autres références à ce sujet seront faites en relation avec les preuves archéologiques pour la date de la construction.
Ceux-ci sont nommés d’après le célèbre antiquaire du XVIIe siècle, John Aubrey, qui a marqué sur son plan en 1666 un certain nombre de « dépressions » ou « cavités » juste à l’intérieur de la banque. Il a suggéré qu’ils auraient pu être le site d’un ancien cercle de pierres comme celles d’Avebury. Ces dépressions n’étaient pas visibles au moment des investigations du colonel Hawley en 1920, mais il les redécouvrit en sondant avec une tige d’acier les endroits marqués par Aubrey. Il a ensuite fouillé 32 de ces sites et a découvert, grâce à ses fouilles et à ses sondages, qu’il y avait un anneau complet de trous. Les 32 trous creusés sont maintenant marqués par des disques de craie blanche sur le sol.
Ces trous Aubrey sont sur la circonférence d’un cercle de 288 pieds de diamètre, dont le centre est à environ 2 1/2 pieds au sud du centre du cercle de Sarsen. Il semble y avoir en tout 56 trous d’Aubrey, espacés avec une précision considérable, à un intervalle de 16 pieds 2 pouces d’un centre à l’autre autour du cercle. Les trous sont à peu près circulaires et, selon le guide officiel, ils ne varient pas beaucoup en taille ou en forme, étant plutôt de plus de 3 pieds de profondeur et 5 pieds de diamètre. La plupart des 32 qui ont été fouillés contenaient les restes d’une crémation humaine. Des éclats de pierre bleue et de la poterie romano-britannique y ont également été trouvés.
Il ne fait aucun doute que les trous contenaient à l’origine des montants. Les archéologues, cependant, sont divisés sur la question de savoir s’il s’agissait de bois ou de pierre. Il est souligné dans l’Official Guide Book (p. 18) que « la craie solide, qui se trouve très près de la surface à Stonehenge, a dans de nombreux cas été écrasée sur les lèvres de ces trous, ce qui suggère que les montants qui pouvaient autrefois s’y trouver ont été abaissés ».
Plus loin, il est dit qu'« une suggestion très intéressante a été faite que les pierres Prescelly formaient à l’origine ce simple cercle de pierres brutes, qui plus tard ont été enlevées et habillées pour être érigées dans leur position actuelle à l’intérieur du cercle et du fer à cheval des trilithes de Sarsen ». S’il en est ainsi, cela jette beaucoup de lumière sur la question de la date de construction du grand cercle de Sarsen.
La plupart des trous ont une rampe ou une pente d’un côté. Celui-ci descend sur une partie du chemin dans le trou, et a sans doute été utilisé, comme les rampes des pierres de Sarsen, pour mettre les montants en position.
Les crémations semblent avoir été placées dans une pelle peu profonde dans la partie supérieure de la rampe, et avoir glissé, probablement lorsque les montants ont été enlevés. Les restes ne sont pas en une masse compacte, mais sont généralement diffusés vers le bas de près du haut vers le bas. Les crémations sont considérées comme dédicatoires plutôt que sépulcrales, car les os n’étaient pas toujours suffisants pour un corps complet, et aucune relique n’a été trouvée avec eux.
La partie centrale du remplissage des trous d’Aubrey s’est avérée être généralement plus terreuse que les bords, et contenait des reliques tardives, telles que la poterie romano-britannique, à une plus grande profondeur. Aucun éclat de pierre n’a été trouvé au fond des trous d’Aubrey. Ceci est considéré comme une preuve que les pierres de Sarsen et les pierres bleues n’avaient pas été ébréchées lorsque les trous d’Aubrey ont été remplis (voir Stonehenge et sa date, R.H. Cunnington, 1935, pp. 26, 28).
La zone sur laquelle se dresse le monument de Stonehenge est entourée d’un fossé circulaire, avec un talus bas qui le jouxte sur le côté intérieur. Les cercles du fossé et de la berge ont été dessinés avec précision, et ils ont dû être construits avant que les pierres de Sarsen ne soient érigées. Sinon, il aurait été impossible d’utiliser une corde de piquetage pour tracer les cercles.
Le centre du fossé et du banc est le même que celui du cercle d’Aubrey, à 2 3/4 pieds au sud du centre du cercle de Sarsen. Les rayons sont les suivants :
Bord extérieur du fossé – 187 pieds
Jonction du fossé et du talus – 168 1/2 pieds
Centre du talus – 159 1/4 pieds
Bord intérieur du talus – 150 pieds
Le haut du fossé et le talus sont donc tous deux de la même largeur, soit 18 1/2 pieds.
La banque est maintenant très usée et le fossé est plus qu’à moitié rempli. La hauteur moyenne de la berge au-dessus du niveau général de l’enceinte n’est que de 14 pouces, et le fond du fossé est maintenant de 2 pieds 3 pouces au-dessous de ce niveau général. On considère que lorsqu’il a été fraîchement creusé, le fossé avait entre 4 et 5 pieds de profondeur et 6 ou 7 pieds de large au fond. Comme la largeur au sommet est de 18 1/2 pieds, cela donne une pente d’environ 37 degrés.
D’après l’expérience acquise dans le domaine de l’ensablement des fossés, on considère que le fossé s’est envaseté rapidement au début, une grande partie du limon grossier au fond étant due au dégel des surfaces gelées les matins d’hiver, provoquant la désintégration et le glissement des fragments crayeux vers le fond. Après cela, un matériau fin et crayeux serait lessivé et formerait une fine couche au-dessus du limon grossier.
Ce processus a une incidence sur les reliques archéologiques trouvées dans le fossé de Stonehenge. La couche supérieure est maintenant constituée de gravats de craie terreuse de 15 à 18 pouces d’épaisseur, y compris le gazon moderne. En dessous se trouvent quelques centimètres de limon fin, « séparés brusquement de la couche supérieure », puis il y a environ un pied de limon grossier au fond.
L’entrée principale du côté nord-est était à l’origine une chaussée de 37 1/2 pieds de large, où le fossé n’a jamais été creusé. il y avait une autre chaussée, appelée la chaussée sud, presque exactement au sud du monument, où le fossé n’a pas non plus été creusé. Il s’agissait probablement d’une entrée cérémonielle, car elle est exactement dans l’alignement de la courte pierre de Sarsen n° 11, qui n’était pas pourvue d’un linteau. Il a été suggéré qu’il s’agissait de permettre aux processions avec des bannières d’entrer dans le cercle de Sarsen.
En ce qui concerne la chaussée nord-est, il semble que très peu de temps après que le fossé ait été creusé, les 30 derniers pieds ont été remplis de craie blanche propre, enfoncée durement. Cela montre que les remplissages avaient été intentionnels, afin d’élargir l’entrée, et de la rendre presque identique à l’avenue, qui a 71 pieds de large.
Le colonel Hawley a découvert dans ses fouilles qu’à l’endroit où le creusement initial du fossé s’est terminé, il y avait un mur presque perpendiculaire de craie solide, de 4 pieds 9 pouces de haut. Il est évident que cette partie du fossé a été remblayée très peu de temps après avoir été excavée, et avant le début de l’envasement, car il n’y a aucun signe de mélange terreux dans le remplissage.
Il ne fait aucun doute que la chaussée a été laissée intacte pour fournir une entrée par laquelle la plupart des grandes pierres de Sarsen ont pu être transportées, et en relation avec le transport, une entrée plus large a pu être jugée souhaitable ; d’où le pilonnage dur du matériau ; et, de plus, elle était alors symétrique avec l’avenue dont la construction complète était probablement une étape ultérieure des travaux.
L’Avenue, la pierre de Friar’s Heel et la pierre de l’abattage
L’Avenue
Il s’agit d’une large route préhistorique qui s’étend du monument, d’abord sur près de 600 mètres en ligne droite vers le nord-est (direction du lever du soleil au milieu de l’été), à partir du bord extérieur du fossé. La partie centrale a une largeur de 47 pieds et est légèrement surélevée au-dessus du niveau général. De chaque côté de cette route centrale se trouve un talus bas s’élevant d’un fossé peu profond. Ces deux fossés ont maintenant chacun environ 12 pieds de large et environ 2 pieds de profondeur. Les fouilles ont montré que les fossés étaient à l’origine construits en forme de V et qu’ils avaient alors une profondeur d’environ 3 pieds. Ils sont distants de 71 pieds d’un centre à l’autre.
L’ancienne avenue prend un léger cours descendant, avec la pente générale du terrain, jusqu’à ce qu’elle atteigne le fond de la vallée. Ensuite, il se divise en deux branches ; une branche tourne vers le haut dans la direction de l’est et se dirige vers Amesbury, à 2 1/2 milles de distance. L’autre branche va vers la gauche, et on pense qu’elle rejoint le « Cursus », une grande zone ovale qui est considérée comme ayant peut-être été un ancien hippodrome, ou un terrain pour des compétitions et des sports. Il a été suggéré qu’il aurait également pu être utilisé pour des foires préhistoriques ou comme place de marché.
En approchant du fossé circulaire de Stonehenge, les berges et les fossés de l’avenue deviennent moins profonds et cessent à moins de 10 pieds de celui-ci. La ligne centrale de l’avenue passait au centre entre les pierres d’entrée n° 30 et 1 du cercle de Sarsen, à travers le centre du cercle et à mi-chemin à travers les montants du grand trilithe central.
Il sera démontré plus tard qu’il est correct, et qu’il est important, car il s’agit du véritable axe de Stonehenge. Il est clair que cette ligne centrale a été intentionnellement dirigée vers le point du lever du soleil au milieu de l’été, lorsque le cercle de Sarsen de Stonehenge a été construit.
La pierre du talon du frère
Il s’agit d’une très grande pierre de Sarsen, s’élevant à une hauteur d’environ 16 pieds au-dessus du sol. Il mesure 8 pieds de large près du centre, mais se rétrécit jusqu’à une pointe émoussée au sommet. Il a environ 4 pieds d’épaisseur et est encastré dans le sol dans une position penchée vers le monument. Il est situé dans l’avenue à environ 6 pieds à droite, ou sud-est, de la ligne centrale, et à une distance de 256 pieds du centre du monument.
Diverses explications ont été données à propos du nom, mais la plus probable semble être qu’il était dérivé du nom celtique original « Cloch Na Freas Heol », ou « Pierre du soleil levant ». Bien sûr, il n’est pas aligné avec le point du lever du soleil vu du centre du monument ; et dans les temps anciens, il devait être à près de 1 1/4 degré à l’est du point du lever du soleil, indiqué par la direction de l’axe et la ligne centrale de l’avenue.
Lorsque le soleil se serait complètement levé au-dessus de l’horizon, il y aurait eu une certaine position à l’intérieur du cercle de Sarsen, d’où le soleil apparaîtrait à ce moment-là verticalement au-dessus de la pierre du talon du frère. D’autre part, il peut avoir été utilisé comme gnomon pour projeter une ombre, dont la position a été observée, le jour et près du jour du solstice d’été.
C’est ainsi que E. Duke, dans son livre Druidical Temples, 1846, p. 133, dit : « C’était un gnomon destiné à observer le lever du soleil le matin propice du solstice d’été. » Il sera fait référence à cela en relation avec l’astronomie de Stonehenge.
Dans le Guide officiel de Stonehenge, par Frank Stevens, p. 21, il est dit que « D’autres indications de l’importance de cette pierre, pour les constructeurs, étaient à venir lorsque les fouilles du côté ouest ont révélé une tranchée circulaire d’environ 30 pieds de diamètre qui l’entourait. La partie orientale de celle-ci avait été détruite par la chaussée actuelle.
Pierre d’abattage
Il s’agit d’un grand bloc de Sarsen posé à plat et en partie encastré dans le sol. Il se trouve à environ 6 pieds à l’est de l’axe et à 150 pieds du centre du monument. Il se trouve dans le sens de la longueur, presque parallèle à l’axe, et sa longueur est de 21 pieds 6 pouces, sa largeur de 6 pieds 9 pouces, son épaisseur de 2 pieds 9 pouces. Il a évidemment été mal nommé, car il a été démontré qu’il se tenait debout vers le milieu du XVIIe siècle, et qu’il formait l’une des deux grandes pierres d’entrée.
Le trou dans lequel se trouvait le compagnon a été creusé par le colonel Hawley en 1920. Son centre était à environ 8 pieds 6 pouces de la partie la plus proche de la pierre de l’abattage du côté nord-ouest, et à environ 152 pieds 6 pouces du centre du cercle de Sarsen, c’est-à-dire juste sur le banc, et non loin de son bord intérieur.
Le colonel Hawley rapporta : « Nous sommes tombés sur un très grand trou d’environ 10 pieds de diamètre sur 6 1/2 pieds de profondeur que nous avons progressivement creusé. Nous avons trouvé une pièce de monnaie de Cladius Gothicus dans la couche supérieure, mais rien d’intéressant jusqu’à ce que nous atteignions le fond où deux pics en corne de cerf reposaient contre le côté. Il ne fait aucun doute qu’une grosse pierre se trouvait autrefois dans le trou. (Remarque : Claudius Gothicus était empereur romain de 268 à 270 après J.-C.)
La plus ancienne estampe de Stonehenge, datée de 1575 après J.-C., montre deux grandes pierres à l’intérieur du travail de terre circulaire, une de chaque côté de l’entrée. Ceux-ci sont également confirmés par les rapports d’Inigo Jones, vers 1621, et de John Aubrey, 1666, qui indiquent également une paire plus petite de pierres d’entrée verticales en plus des plus grandes. À l’époque d’Aubrey, cependant, l’une des plus petites de ces quatre pierres semble avoir disparu.
Les recherches archéologiques à Stonehenge, qui ont été très étendues, ont conduit à des divergences d’opinion remarquables concernant la date de sa construction.
Avant d’approfondir cette question, il convient de préciser que, qu’il y ait eu ou non un cercle de pierres bleues antérieur à la construction du grand cercle de Sarsen, c’est la date de ce dernier, et son axe, qui sont des considérations essentielles du point de vue de l’astronomie de Stonehenge.
Au XVIIe siècle, Aubrey, Stukeley et d’autres étaient fortement convaincus que Stonehenge était un temple druidique, et c’était la croyance générale au XIXe siècle. Les chercheurs ultérieurs, cependant, ont de plus en plus favorisé une date beaucoup plus ancienne, et ont interprété les preuves comme correspondant à la fin du Néolityique ou au début de l’âge du bronze, avec la date d’environ 1800 av. J.-C., ou peut-être de l’âge du bronze moyen, environ 1200 av. J.-C.
Le fait que des marteaux ou des maillets en pierre aient été utilisés pour travailler les pierres de Sarsen, et que des pics en corne de cerf aient été utilisés pour creuser, semble soutenir une date très ancienne. Mais il a été souligné que les ciseaux métalliques auraient été trop mous pour travailler des pierres aussi dures que les pierres de Sarsen et les pierres bleues ; et les outils en silex et en quartzite étaient les plus efficaces. De plus, pour creuser, des pics en corne de cerf auraient été utilisés à n’importe quel moment, et sont même utilisés de nos jours dans des régions isolées d’Écosse.
À l’appui de la date très ancienne, l’analogie avec de nombreuses structures mégalithiques anciennes dans les îles britanniques et sur le continent, semblait indiquer une date tout aussi précoce pour Stonehenge. D’autre part, cependant, il a été démontré que le caractère architectural de Stonehenge est bien au-delà de celui des structures mégalithiques primitives, et est plus caractéristique de la période ultérieure.
Les recherches astronomiques de Sir Norman Lockyer en 1901 ont soutenu la date précoce de Stonehenge et ont suscité un grand intérêt dans les cercles archéologiques. Nous l’examinerons en détail dans la section suivante, relative à l’astronomie de Stonehenge.
Les archéologues en général admettent que l’axe de Stonehenge a dû être intentionnellement aligné sur la position du soleil au lever du soleil le jour du solstice d’été. Par conséquent, la date astronomique trouvée par Sir Norman Lockyer avait beaucoup de poids auprès de ceux qui interprétaient les données archéologiques comme indiquant la construction de Stonehenge à la fin de la période néolithique, ou au début de l’âge du bronze ; Et jusqu’en 1925, c’était une opinion commune parmi les archéologues.
Mais en 1920, les fouilles du colonel Hawley ont mis au jour beaucoup de nouveaux matériaux qui, avec le temps et l’étude plus approfondie des preuves, ont entraîné un changement dans les perspectives archéologiques. Les preuves ont été exposées en détail par le colonel R.H. Cunnington dans son livre Stonehenge and its Date, publié en 1935. La conclusion à laquelle il parvient est que la grande quantité de poterie de l’âge du fer et romano-britannique trouvée à Stonehenge conduit à la croyance que la date de construction doit être ramenée à « l’âge du fer des Celtes et aux 4ème et 5ème siècles av. J.-C. » Pour un compte rendu complet de ces preuves, on peut se référer au livre du colonel Cunnington, Mais les brèves notes suivantes serviront à en indiquer la nature.
Tout d’abord, nous ferions mieux de donner quelques indications sur les dates approximatives des différentes périodes, ou âges, reconnues par les archéologues dans leur datation des spécimens de poterie et d’autres matériaux trouvés à Stonehenge.
La première période, à laquelle les plus anciens de ces spécimens sont généralement rapportés, est le Néolithique, ou « nouvel » âge de pierre, marqué par certains types d’outils en pierre, de poteries et de reliques sépulcrales. Cette période s’est terminée vers 1800 av. J.-C., lorsque l’Angleterre a été envahie par le « peuple du bécher ». Ces « Beaker Folk » sont venus du continent et se sont répandus à l’intérieur des terres à travers le sud et l’est de l’Angleterre. Où qu’ils aillent, on en trouve des traces dans les « Gobelets », ou coupes à boire, qu’ils fabriquaient avec l’argile locale. Des spécimens de cette poterie préhistorique sont largement diffusés. Ils ont également introduit des armes en bronze et d’autres articles en bronze, ce qui a introduit en Angleterre « l’âge du bronze ».
On considère que le début de l’âge du bronze dure d’environ 1800 à 1500 av. J.-C. L’âge du bronze moyen peut être considéré comme la période de 1500 à 1000 av. J.-C., et l’âge du bronze tardif de 1000 av. J.-C. à environ 700 av. J.-C. Il chevauche ensuite le début de l’âge du fer, lorsque l’utilisation du fer a été introduite en Grande-Bretagne.
L’âge du fer en Grande-Bretagne, avant l’arrivée des Romains, est subdivisé en trois périodes, connues sous le nom d’âge du fer A, de l’âge du fer B et de l’âge du fer C. On considère que l’âge du fer A commence vers 700 av. J.-C. Cette première division de l’âge du fer est également connue sous le nom de période Hallstatt. Le nom est dérivé du village de Hallstatt, dans le Tyrol autrichien, où un grand nombre des premières reliques de l’âge du fer a été mis au jour.
La date de l’arrivée en grand nombre des envahisseurs de Hallstatt en Grande-Bretagne n’est pas considérée comme bien antérieure à 600 av. J.-C., bien que leur influence se soit fait sentir quelque temps avant cette date.
La période allant de 500 av. J.-C. au début de l’ère chrétienne comprend les deux sous-divisions ultérieures de l’âge du fer B et de l’âge du fer C. On l’appelle aussi la période de La Tène. Ce nom est tiré d’un site sur le lac de Neuchâtel en Suisse, où des reliques typiques de ces personnes ont été identifiées. Elle est marquée par de nouveaux types d’armes et d’ornements, et par de nouveaux types de poterie. Ces habitants de La Tène sont identifiés comme les premiers Celtes, qui étaient connus des Grecs vers 500 av. J.-C.
Il est établi qu’à cette époque, un grand nombre d’entre eux du Rhin inférieur avaient trouvé leur chemin vers les Pyrénées et le nord de l’Espagne, qui était reliée à la partie sud-ouest de la Grande-Bretagne par le commerce de l’étain. Beaucoup sont venus en Angleterre par cette route, mais le plus grand nombre a traversé la France et la Bretagne, et a envahi l’Angleterre depuis la Bretagne au 4ème siècle avant JC. C’étaient des gens très vigoureux, et on dit que les Celtes de La Tène dominaient, tout en se mêlant à la population indigène.
L’âge du fer C a commencé au 1er siècle av. J.-C., avec l’invasion de l’Angleterre par les Belges, depuis la Gaule belge. La période romano-britannique est incluse dans l’âge du fer C et se poursuit à l’époque romaine.
Il convient de souligner que la poterie et d’autres articles caractéristiques de ces diverses périodes peuvent être antérieurs à la date de l’invasion, en raison de l’influence du commerce continental. De plus, des articles typiques de certaines époques peuvent avoir été utilisés à des périodes ultérieures en raison de la survie. Ainsi, pendant l’âge du fer A, « il y avait une survivance dans certaines régions de l’industrie du silex ». De nombreux types sont mentionnés, y compris « pierres de marteau et pilons », ainsi que « des pics de bois de cerf se produisent ». (Voir Archéologie en Angleterre et au Pays de Galles, par Kendrick et Hawkes, 1932, pp. 167-168). Cela a une incidence sur l’occurrence de tels articles à Stonehenge.
Ce qui suit est un bref compte-rendu, tiré principalement des travaux du colonel Cunnington, ainsi que d’autres sources, des preuves archéologiques trouvées à Stonehenge, donnant un indice sur la date de sa construction.
Le fossé et la berge : Il a déjà été fait mention de l’ensablement rapide du fossé après qu’il a été creusé pour la première fois, avec du limon grossier au fond, d’environ un pied d’épaisseur, recouvert de quelques pouces de limon fin, celui-ci étant séparé brusquement de la couche supérieure, « consistant en moellons de craie terreuse, de 15 à 18 pouces d’épaisseur, y compris le gazon moderne. Le limon contient très peu de reliques ; des os d’animaux et des silex travaillés, deux petits morceaux de poterie non identifiés, et au fond un certain nombre de pics en corne de cerf et des silex grossièrement ébréchés. Le colonel Hawley a fouillé 180 pieds du fossé, et les quelques reliques trouvées dans la vase ne jettent pas de lumière définitive sur la date.
Les silex et les pics en corne de cerf ont été considérés par certains archéologues comme une preuve de datation néolithique ou de l’âge du bronze, mais d’après ce qui a été établi sur l’utilisation des silex et des pics en corne de cerf au début de l’âge du fer, la présence de ces articles n’implique pas nécessairement une date antérieure.
Quelques petits morceaux de poterie Beaker ont été trouvés sur le limon fin, et en partie encastrés dans celui-ci, mais ils ne sont pas assez nombreux pour être considérés comme des preuves suffisantes pour une construction de l’âge du bronze, car des fragments occasionnels de cette poterie sont trouvés presque partout dans le sol de la plaine de Salisbury, où des fouilles approfondies ont été effectuées.
L’Official Guide Book mentionne un « petit poinçon en bronze de la fin de la saison, vers 500 av. J.-C. (le seul outil réel de l’âge du bronze trouvé à ce jour) ». Cela a été trouvé dans la terre au-dessus de la vase de craie. Il peut, bien sûr, être d’une date ultérieure, par survie, mais pas d’une date antérieure à la période à laquelle il appartient.
La couche supérieure du fossé, représentant la croissance du gazon après l’envasement, ainsi que l’accumulation de terre pendant de nombreux siècles, contient de nombreuses reliques, y compris des poteries de toutes les époques, du bronze ancien au romano-britannique. De plus, les éclats de pierre sont abondants dans toute cette couche.
Dans les 180 pieds du fossé creusé par le colonel Hawley, 19 sections ont été creusées, et des poteries romano-britanniques ont été trouvées dans chacune d’elles. Une chose remarquable est « l’absence presque totale de tout ce qui est postérieur au romano-britannique ». Cela montre la fréquence relative des visites des peuples de la période romano-britannique, par rapport à ceux qui sont venus après eux, jusqu’à l’époque moderne.
Le total de chaque type de poterie est le suivant : « Poterie normande, 3 ; Romano-Britannique, 136 dans 17 sections, et quelques-uns dans les deux autres, ou disons 145 en tout (à l’exclusion des fragments d’un pot de vaisselle de la Nouvelle-Forêt, qui ont été trouvés ensemble) ; vaisselle grossière généralement décrite comme antérieure en date, 36 ; de la vaisselle noire grossière trouvée dans une section, et décrite comme datant principalement de l’âge du bronze, 30 ; Âge du bronze, 6 ; Le bécher, l’un dans la couche supérieure, et les deux groupes associés, (de 10 et 12 petits morceaux), déjà mentionnés, reposent sur le limon.
Le colonel Cunnington fait remarquer que la poterie de l’âge du bronze est rare, pas plus qu’on n’aurait pu en trouver dans n’importe quel sol du voisinage, et que les principaux ingrédients sont la poterie grossière non spécifiée ou douteuse, et la poterie romano-britannique. Il pense qu’il est probable que la « vaisselle grossière d’une date antérieure » puisse être du début de l’âge du fer, et qu’elle se trouve généralement à un niveau inférieur à celui de l’époque romano-britannique.
La plupart des poteries de la couche supérieure du fossé vont de l’âge du fer A à l’âge romano-britannique, et « il n’y a aucune raison de supposer que la couche supérieure est antérieure à celle de la date ». Il souligne également que plusieurs crémations ont été trouvées dans le fossé, la plupart dans la vase, et donc plus tardives que le fossé. Il y en avait un, cependant, sur le sol ou enfoncé dans le sol sans aucun signe d’intrusion, ce qui semble avoir été contemporain. Comme les crémations ne sont connues qu’après le début de l’âge du bronze, cela fournit des preuves d’une date ultérieure.
Le banc n’a pas fait l’objet de fouilles archéologiques, à l’exception de deux tranchées étroites qui le traversent et du fossé. La Banque est donc un terrain prometteur pour l’exploration future. Le sol de surface à l’intérieur du banc est décrit comme étant semblable à la couche supérieure du fossé, contenant des reliques de toutes les dates mélangées dans n’importe quel ordre. La grande quantité de poteries romano-britanniques trouvées ici est commentée par M. Kendrick. Comme il le dit, c’est « bien plus que ce que l’on pourrait attendre des voyageurs visitant le site pour voir une ruine ». C’est-à-dire qu’au début de l’époque romaine britannique, Stonehenge était à l’apogée de sa renommée et de son utilisation, et n’est donc probablement pas construit plus de quelques siècles plus tôt.
De toute évidence, la banque a été construite à partir de la terre jetée à l’origine lorsque le fossé a été creusé. Si l’on tient compte de l’usure de la berge d’environ 4 ou 5 pouces au cours des siècles qui ont suivi sa construction, le contenu cubique de la berge au moment de sa construction correspondrait à celui du fossé.
Un point important, qui jette de la lumière sur les dates relatives de la construction de la banque et du fossé, et du grand cercle de Sarsen, est celui qui a été mentionné précédemment dans la description du fossé. Pour l’élargissement de la chaussée de l’entrée nord-est au-dessus du fossé, de 30 pieds supplémentaires (de 37 1/2 pieds à 67 1/2 pieds), très peu de temps après le creusement initial du fossé jusqu’à ce point, et son but évident de donner plus d’espace pour le transport des grandes pierres de Sarsen dans l’enceinte de Stonehenge, montre que le fossé et le talus ont dû être construits à la même date, et comme une opération préliminaire immédiate avant la construction du cercle de Sarsen. La datation correcte du fossé nous aiderait donc à déterminer la date de construction du cercle de Sarsen.
Trous d’Aubrey : Le colonel Cunnington dit qu’il y a peu de preuves de date dans les trous d’Aubrey. Rien de datable n’a été trouvé près du fond, et seules quelques reliques se trouvaient dans la couche supérieure. La poterie romano-britannique peut se trouver aussi bas que 2 pieds sous la surface, ou 8 ou 9 pouces sous le niveau de la craie solide environnante. Il semble probable que les trous n’aient pas été remplis avec des matériaux serrés, car les dépressions ont été remarquées par Aubrey au XVIIe siècle.
Au cours des deux siècles et demi qui suivirent, cependant, ces dépressions se comblèrent, de sorte qu’elles ne furent découvertes par le colonel Hawley qu’en sondant les positions indiquées par le plan d’Aubrey de 1666 après J.-C. Dans le Guide officiel, il est dit que
Parmi les découvertes dans les trous d’Aubrey figuraient des « fabricants » de silex, utilisés dans la fabrication d’outils en silex, et d’éclats de silex ; Certains d’entre eux ont été remplacés sur les noyaux dont ils ont été retirés, ce qui montre que le travail a été fait sur place.
En plus de ceux-ci, il y avait des haches et des marteaux en pierre Prescelly et des fragments de poterie de l’âge du bronze. L’un d’entre eux est d’un intérêt particulier ; il s’agit d’une partie d’un récipient avec des cornes perforées, qui pourrait avoir été une « coupe d’encens » de l’âge du bronze moyen.
Une photo de cette « Coupe d’Encens » des trous d’Aubrey est donnée à la page 39 du Guide officiel.
Parmi les crémations autour des trous d’Aubrey, il y avait "des épingles en os, bien finies, certaines portant des traces de feu, et une tête de masse de l’âge du bronze magnifiquement finie en gneiss hornblendique, une pierre étrangère à la région mais trouvée en Bretagne et aussi en Écosse. Cela ne montre aucune trace d’usure, et pourrait donc avoir été « cérémoniel ».
Dans le sol entre les trous extérieurs de Sarsens et d’Aubrey, les spécimens archéologiques suivants sont répertoriés :
Des outils en silex grossièrement ébréchés, des poteries de l’âge du bronze, des poteries du début de l’âge du fer (vers 400 av. J.-C.), des « compteurs » ou des disques de poterie pour jouer à un jeu, trois pièces de monnaie romaines, une fibule romaine (350 à 400 ap. J.-C.), un article de toilette romain, un ornement de ceinture en argent anglo-saxon, une pièce de monnaie d’Ethelred II frappée à Londres, un ornement de harnais normand, un gruau d’Henri II, coupé pour en faire un demi-gruau, et un petit pendentif de cloche, peut-être d’un piégeage de chevaux.
Trous en Z et en Y : Ils contiennent un grand nombre de fragments de poterie romano-britannique, avec une proportion beaucoup plus faible de poterie de l’âge du bronze.
Dans les trous en Z, le nombre total de fragments de poterie romano-britannique énumérés par le colonel Hawley est de 190, et celui de la poterie de l’âge du bronze, de 27.
Dans les trous en Y, il y avait 206 fragments de poterie romano-britannique et 35 fragments de l’âge du bronze.
Ainsi, dans les trous Z et Y, les spécimens romano-britanniques sont plus nombreux que ceux de l’âge du bronze d’environ 6 contre 1. Certains des fragments de poterie inclus dans la rubrique romano-britannique ont cependant été identifiés comme étant La Tène.
Une découverte importante, portant sur la date des trous Z et Y, a été la tombe d’un homme de La Tène, près de l’un des trous Y, Y11. Cela a été mentionné par M. T.D. Kendrick comme une preuve certaine de la construction tardive du monument.
Nombre de fragments de poteries de différentes époques
Une analyse des fragments énumérés par le colonel Hawley, dans ses fouilles à Stonehenge entre les années 1919 et 1926, couvrant environ la moitié de la région de Stonehenge, donne le nombre total suivant de diverses sortes de poteries, qu’il a trouvées, à l’exclusion de la période moderne, qui n’a pas été compilée :
Âge du bronze, y compris la poterie « bécher » ou du début de l’âge du bronze – 250
Début de l’âge du fer, avant la période romano-britannique – 85
Romano-britannique – 925
Normand et médiéval – 116Total = 1376
Ces chiffres montrent, tout d’abord, que Stonehenge était très fréquenté à l’âge du bronze. Il faut s’y attendre, car dans le voisinage immédiat de Stonehenge, il y a environ 300 tumulus ronds, ou anciens monticules sépulcraux.
Frank Stevens souligne dans Stonehenge Today and Yesterday, p. 47, que
ils semblent se presser autour du Cercle, comme le font les tombes dans un cimetière de campagne autour de l’église.
Cela ne peut guère être accidentel ; il semblerait plutôt que les Brouettes aient atteint leur plus haut niveau de développement dans la plaine de Salisbury et la région de Stonehenge, et aient formé une vaste nécropole autour du cercle... Ils justifient l’hypothèse selon laquelle le caractère sacré du site rendait l’endroit particulièrement attrayant pour l’enterrement.
Les tumulus ronds sont des tumulus funéraires typiques de l’âge du bronze. Il n’y a que deux Long Barrows, caractéristiques de la période néolithique, près de Stonehenge ; mais il est à remarquer que le tumulus rond n’appartient pas exclusivement à l’âge du bronze. Dans Archaeology in England and Wales, 1932, p. 109, les auteurs, MM. Kendrick et Hawkes, disent des tumulus ronds que « certains ont été érigés au début de l’âge du fer, d’autres à l’époque romaine, et d’autres dans l’Angleterre saxonne et viking ».
C’est ainsi qu’ils ont persisté pendant longtemps, bien qu’ils aient été spécialement associés à l’âge du bronze ; et un compte rendu de ce caractère principalement de l’âge du bronze, la présence d’un si grand nombre de ces tumulus ronds et la quantité considérable de poteries de l’âge du bronze trouvées dans la région de Stonehenge, est cohérent avec l’opinion de nombreux archéologues selon laquelle, avant le monument actuel, il y en avait un plus ancien, à savoir, un cercle de pierres bleues brutes ou non taillées, apporté du sud du Pays de Galles pendant l’âge du bronze.
La prépondérance des fragments de poterie romano-britannique à Stonehenge, avec un petit nombre de fragments du début de l’âge du fer, suggère la probabilité d’une reconstruction dans la forme actuelle à une période peu antérieure à l’époque romano-britannique. Si la reconstruction a eu lieu quelques siècles avant la période romano-britannique, disons entre 300 et 400 av. J.-C., elle expliquerait à la fois l’apparition de la poterie du début de l’âge du fer, la période de La Tène, et aussi celle de la période romano-britannique, au cours de laquelle elle a atteint son utilisation et son importance maximales.
Conditions climatiques indiquées par les coquilles d’escargots
Le colonel Cunnington utilise également les preuves des escargots qui ont été trouvés à Stonehenge. Il fait référence à la pratique des fouilleurs de travaux de terrassement préhistoriques,
en soumettant des échantillons de terre pour l’analyse de leur contenu en coquille d’escargot. Les escargots sont très petits, presque microscopiques, et appartiennent à un grand nombre d’espèces, dont certaines aiment les conditions humides, et d’autres sèches ; Et, en comptant le nombre de chacun, il est possible de dire à quoi ressemblait le climat lorsque le terrassement a été fait, et si les environs étaient ouverts sur terre ou boisés.
D’après ce genre de preuves, qui sont très cohérentes, « il semble prudent de dire que le néolithique et le début de l’âge du bronze dans le sud de l’Angleterre étaient décidément plus humides qu’aujourd’hui, et tous les travaux de terre à cette époque doivent avoir des escargots qui aiment l’humidité. »
À partir de ce moment-là, le climat devient plus sec. À Stonehenge, « plusieurs échantillons de terre ont été prélevés dans le fossé et dans les trous de poteaux, et dans chacun d’eux, il y avait une absence totale des escargots qui aiment l’humidité ». Cela indique que les conditions étaient celles d’un climat sec, le même qu’aujourd’hui, et que le fossé, et d’autres travaux majeurs qui l’accompagnaient, à savoir le banc, les quatre stations et le grand cercle de Sarsen lui-même, avec ses grands trilithes intérieurs et d’autres caractéristiques uniques, ont été construits à une période relativement tardive, et non à l’âge néolithique ou à l’âge du bronze.
Architecture de Stonehenge
M. T.D. Kendrick, dans son livre les Druides, discute assez longuement de l’architecture de Stonehenge. Il décrit Stonehenge comme « une réalisation architecturale qui dépasse complètement tout ce qui a été tenté jusqu’à présent dans la tradition mégalithique ordinaire ».
Outre des méthodes spéciales pour tailler et tailler les grandes pierres de Sarsen, les constructeurs de Stonehenge « ont utilisé un nouveau dispositif inconnu dans l’architecture mégalithique de l’Europe ». C’était la méthode classique utilisée dans la construction des temples en Grèce et à Rome pour assembler les membres d’une colonne par la « serrure à cheville et à douille ». On le voit à Stonehenge dans la méthode à tenon et mortaise pour fixer solidement les pierres de linteau aux montants, à la fois du grand cercle de Sarsen et de la formation en fer à cheval des trilithes à l’intérieur du cercle.
M. Kendrick dit : « Je répète donc que la mortaise et le tenon trahissent l’influence indirecte de l’architecture classique, et ramènent la date du monument à la période de La Tène. » Il soutient cet argument d’un autre point de vue tout aussi fort, concernant la religion du druidisme.
Par druidisme, il entend la première religion celtique introduite en Grande-Bretagne par le peuple de La Tène, identifiée aux premiers Celtes, qui ont envahi la Grande-Bretagne en grand nombre à partir de la région du Rhin inférieur, à partir de l’an 500 av. J.-C. environ. Il dit dans Les Druides, p. 155 :
Si Stonehenge n’était pas un temple du druidisme, alors il devait être une ruine désaffectée à l’époque de La Tène, lorsque le druidisme était la religion du pays.
Mais est-ce que toutes les poteries britanniques et romano-britanniques et la sépulture réelle d’un homme de La Tène dans leur région (Antiquaires ; Journal V. 31) suggèrent vraiment la visite des voyageurs pour regarder une ruine ? Je ne pense pas. Et je demanderais quelle était la religion de cet homme de La Tène, de ce premier Anglais qui a été enterré là, si ce n’était pas du druidisme ?
Et s’il s’agissait de druidisme, n’est-il pas plus probable qu’un croyant serait enterré dans l’enceinte du temple de sa propre foi que dans le sanctuaire en ruine d’une religion oubliée ?
En résumé, la séquence des événements à Stonehenge, très probablement d’après les résultats archéologiques précédents et les commentaires de divers auteurs érudits, semble être la première, qu’il y avait un simple cercle de pierre bleue, avec des entrées de linteau, tout d’abord établi à l’âge du bronze ; et le site de celui-ci était celui des trous d’Aubrey. Le centre de ce cercle se trouvait à 2 3/4 pieds au sud du centre du cercle de Sarsen.
Ce cercle de pierres bleues a duré environ mille ans et a été utilisé dans le système religieux des anciens Bretons, avant l’invasion celtique ou de La Tène. Ces nouveaux venus, après avoir obtenu la domination en Grande-Bretagne, par la suite, c’est-à-dire entre 300 et 400 av. J.-C., ont reconstruit l’ancien temple, sous une forme différente, une partie d’un nouveau et impressionnant temple, dans les ordres suivants :
La disposition de cette longue ligne d’axe du monument et de l’avenue, si précisément dirigée vers le lever du soleil du milieu de l’été, vu de Stonehenge, est le principal point d’importance dans l’astronomie de Stonehenge. Par conséquent, bien qu’il soit d’un grand intérêt, et nécessaire pour comprendre le problème de Stonehenge, d’examiner ses données archéologiques et historiques dans leur ensemble, le reste de cette enquête sera consacré tout d’abord à l’étude des diverses tentatives pour définir le véritable axe de Stonehenge, puis à montrer que, si l’astronomie est également vraiment établie, nous en tirerons nécessairement un résultat pour la date de construction du grand Cercle de Sarsen et de ses annexes en accord étroit avec l’archéologie et l’histoire du monument.
Enfin, nous verrons ensuite que l’astronomie de Stonehenge, tout comme celle du Grand Temple Solaire de Karnak, montre clairement que, tandis que la Formule de Newcomb donne une date de construction totalement inacceptable et erronée pour chacun de ces célèbres monuments de l’Antiquité, la Nouvelle Courbe de l’Obliquité de l’Écliptique, qui a de grandes implications également dans d’autres directions, donne cet accord nécessaire à la fois avec l’archéologie et avec l’histoire.
En effet, en plus du contexte historique général décrit dans les pages précédentes, nous avons la référence spécifique et frappante suivante à la reconstruction de Stonehenge vers l’an 350 av. J.-C. par le célèbre roi britannique Belinus. C’est ce que rapporte R.W. Morgan dans son Histoire de la Grande-Bretagne ancienne. Il dit que le roi Belinus (qui était le frère de Brennus, qui mit Rome à sac en 390 av. J.-C.)
après la conquête de l’Allemagne, fonda Aquilée, où il fut ensuite adoré comme un dieu. De retour par la Gaule, il divisa ses territoires entre ses cinq fils cadets, gardant le gouvernement de la Grande-Bretagne entre ses propres mains. Il employa les dernières années de son long et glorieux règne à légiférer pacifiquement et à construire des ouvrages publics.
Le château de Belen (Billing’s Gate) et le magnifique remblai de la Tamise ont été commencés et achevés sous ce monarque. Il construisit également Caer Leon (à l’origine Caer usc) et répara les temples druidiques de Cor gawr (Stonehenge) et Ambri. Il est mort dans la 80e année de son âge. Son corps fut brûlé et les cendres déposées dans une urne en or au sommet de la plus haute tour de son palais sur la Tamise.
Selon cela, la reconstruction de Stonehenge aurait donc été réalisée vers 350 av. J.-C.
Il ne fait aucun doute que Stonehenge, en plus de ses autres objectifs, a été conçu pour un usage astronomique, associé au maintien de l’ancien calendrier, car il présente ces alignements remarquables de l’axe principal et des « quatre stations », tous définitivement dirigés vers la position du soleil à l’horizon, au lever ou au coucher du soleil, les jours saisonniers et de festival les plus importants de l’année celtique. De ces alignements, celui de l’axe principal du monument, dirigé vers le point du lever du soleil au milieu de l’été à l’horizon nord-est, et vers le coucher du soleil au milieu de l’hiver dans la direction opposée (sud-ouest), est celui sur lequel une détermination astronomique de la date de construction du grand cercle de Sarsen peut être basée avec précision, à condition que nous puissions être sûrs de la position réelle de l’axe.
Cet axe n’a cependant pas été facile à définir avec la certitude souhaitée, en raison de l’état actuel imparfait du monument. Quatre tentatives ont été faites, et avec quatre résultats différents. Nous devons maintenant examiner la question de leur exactitude. Ensuite, nous devons examiner la base astronomique sur laquelle une détermination de date peut être faite.
L’axe de Petrie : La première des quatre tentatives de définition de l’axe de Stonehenge, que nous examinerons, est celle qui a été faite par Sir Flinders Petrie en 1877. Il mesura la position de toutes les pierres dressées et incluit dans son plan cinq autres pierres debout en 1747, dont les positions étaient tirées du plan de Wood de cette date. Il a ensuite tracé un « cercle mesquin » qui, pensait-il, « s’accorde le mieux avec toutes les pierres de Sarsen, en tenant compte de leurs déplacements ». L’axe de Petrie a été fixé par lui comme suit :
Lorsque cette ligne d’axe est produite, elle diffère nettement de la ligne centrale de l’avenue.
À la pierre du talon de Friar, elle est à 1 pied 10 pouces à l’est de la ligne centrale de l’avenue, et frappe la pierre du talon de 10 pouces à l’intérieur de son côté gauche, ou nord-ouest. Il continue ensuite à s’éloigner de la ligne centrale de l’avenue à raison d’environ 11 pouces tous les 100 pieds. Cette grande divergence de l’axe de Petrie par rapport à la direction de l’avenue montre que Sir Flinders Petrie n’a pas reconnu que l’avenue, lorsqu’elle quitte le monument, était elle-même vraiment dirigée vers le point du lever du soleil au milieu de l’été à la date de la construction de Stonehenge.
C’était, en fait, une partie intégrante de l’ensemble du système d’axe de Stonehenge ; Et l’on montrera qu’il s’agissait d’un véritable prolongement de l’axe interne du monument. C’est ce qu’a réalisé et démontré M. E.H. Stone dans son livre The Stones of Stonehenge, publié en 1924.
Le système d’axes complet de Stonehenge, définissant à la fois la position du lever du soleil au milieu de l’été au nord-est et du coucher du soleil au milieu de l’hiver au sud-ouest, à la date de la construction du cercle de Sarsen, est considéré comme une ligne, d’une longueur totale de 14 milles, à partir du château de Grovely, à 6 miles au sud-ouest de Stonehenge (marquant la position du coucher du soleil au milieu de l’hiver vue de Stonehenge), en passant par le cercle de Sarsen
- à mi-chemin entre les pierres sud-ouest 15 et 16
- à mi-chemin entre les montants du Grand Trilithe Central
- par le centre du cercle de Sarsen, et de là
- par le milieu de l’espace entre les pierres d’entrée 30 et 1
- puis le long de la ligne médiane de l’avenue vers l’ancienne fortification de Sidbury au sommet de Sidbury Hill, à 8 miles au nord-est de Stonehenge, où le soleil, vu du monument, s’est levé un jour d’été à la date de la construction du cercle de Sarsen.
Cela a été clairement reconnu par Sir Norman Lockyer, dans son récit de Stonehenge ; et la très légère différence dans l’angle d’azimut des deux extrémités (49° 34' 18 » à l’est du nord pour Sidbury, et 49° 35' 51 » à l’ouest du sud pour le château de Grovely), qu’il cite dans l’Ordnance Survey, n’est pas plus grande que ce qu’il faut attendre de légères différences d’altitude de l’horizon aux deux endroits, affectant la position apparente du point de lever du soleil au solstice d’été et du point du coucher du soleil au solstice d’hiver.
En fait, cela semble être un très bon accord, compte tenu des moyens d’observation disponibles dans les temps anciens.
Cette coïncidence est donc si proche que la conclusion est inévitable, que ces deux points à l’horizon lointain de Stonehenge ont été délibérément établis comme points de repère, pour indiquer les points tournants solstitiels du soleil aux solstices d’été et d’hiver, vus de Stonehenge.
Sir Flinders Petrie était très désavantagé dans l’estimation de la position interne de l’axe du cercle de Sarsen, en raison de la non-reconnaissance de cette caractéristique importante dans l’astronomie de Stonehenge, et en outre, en s’appuyant sur l’analogie, en supposant que l’espace étroit entre les montants des trilithes debout, 12,8 et 12,4 pouces, pourrait être pris comme un guide pour l’espace original entre les montants du grand Trilithe central, qu’il supposait avoir été de 13 pouces.
On a prouvé que c’était une grande erreur, comme on le verra plus tard, par les mesures exactes de la largeur de ces montants, de la longueur de la pierre de linteau et des positions des tenons et des mortaises, qui s’unissent pour donner une mesure exacte de l’espace primitif. Ces mesures montrent donc sans aucun doute que cet espace originel entre les montants du grand Trilithe central était de 3 pieds au lieu des 13 pouces supposés par Sir Flinders Petrie.
Sir Flinders Petrie a également accepté un espacement moyen de 36 pouces entre les pierres comme étant l’espace probable entre la pierre n° 16 et la pierre n° 15 tombée et déplacée à l’extrémité sud-ouest de l’axe ; qu’il a ainsi donné comme la moitié de l’espace moyen, 18 pouces, du côté du n° 16. Il a toutefois exprimé quelques doutes sur cette distance et a déclaré : « C’est très vague. »
Une analyse plus minutieuse de la largeur des pierres et de leur espacement, près de cette extrémité de l’axe, montre que l’estimation de M. E.H. Stone de 5 pieds 2 pouces pour l’espace entre 15 et 16 est essentiellement correcte, et que, comme pour l’entrée nord-est, un espace plus large que la moyenne entre les pierres sud-ouest a été prévu.
D’après ce qui précède, il est évident que le véritable axe de construction de Stonehenge n’est pas seulement définissable à partir de la structure interne du monument, mais qu’il coïncide également avec les extensions du château de Grovely au sud-ouest, et le long de la ligne centrale de l’avenue jusqu’au sommet de Sidbury Hill dans la direction nord-est.
L’axe de Petrie est affecté par des erreurs à ces deux égards, et il est clair que ce n’est pas le véritable axe. Il est donc impossible d’en tirer une véritable date astronomique de construction. L’axe de Petrie pointe dans une direction de 50° 05' 27" à l’est du nord, qui était donc, selon sa mesure, l’azimut à l’est du nord du point du lever du soleil au milieu de l’été lorsque le cercle de Sarsen a été construit. Cela donne la déclinaison solstitielle du soleil, ou ce qui revient au même, l’obliquité de l’écliptique à cette date, à savoir 23° 38' 11". Nous trouvons donc, d’après la formule de Newcomb, que la date correspondante est 471 après J.-C. Cette date est tout à fait inacceptable, compte tenu des résultats archéologiques, comme indiqué précédemment.
Mais il a été démontré dans les recherches astronomiques précédentes que la formule de Newcomb ne donne pas à elle seule la véritable position du soleil dans les temps anciens. Pour obtenir la véritable position du soleil, la formule de Newcomb a besoin d’une correction, fournie par la Nouvelle Courbe de l’Obliquité de l’Écliptique, qui correspond aux anciennes observations solaires, et de manière très frappante, avec le résultat obtenu de l’étude du grand Temple Solaire de Karnak, datant de l’année 2045 av. J.-C.
Nous verrons tout à l’heure qu’elle s’applique également dans le cas du cercle de Sarsen de Stonehenge.
En utilisant cette correction de la formule de Newcomb pour la position du soleil correspondant à l’axe de Petrie, nous obtenons, conformément à la Nouvelle Courbe, la date de 764 ap. J.-C. C’est 293 ans plus tard que la date donnée par la formule de Newcomb, et c’est une date tout à fait impossible pour Stonehenge. La source de l’erreur ne réside pas dans la Nouvelle Courbe de l’Obliquité, mais dans la déviation de l’axe de Petrie par rapport à la véritable direction de l’ancien lever de soleil du milieu de l’été vu de Stonehenge.
Il est à remarquer que la nouvelle courbe donne toujours une date ultérieure à la formule de Newcomb pour une valeur donnée de l’obliquité de l’écliptique, et que cette différence, qui est très grande dans l’antiquité reculée, diminue rapidement à travers les siècles, jusqu’à ce qu’elle devienne nulle à la fin de la courbe, c’est-à-dire en 1850 après J.-C.
On peut donc voir que, pour les besoins de la chronologie ou de l’archéologie, lorsque des observations solaires ont été faites à un solstice et qu’un lien précis avec la position du soleil a été établi, cette méthode astronomique de datation fournit un critère très sensible pour vérifier la véritable date de construction d’un bâtiment tel que le cercle de Stonehenge. le temple de Karnak, ou tout autre temple du même genre.
Nous verrons tout à l’heure, dans le cas de l’axe de Lockyer, qui est très proche de l’axe vrai, la date astronomique de ses observations, d’après la formule de Newcomb, est de 1822 av. J.-C., mais la nouvelle courbe, d’après les mêmes observations, donne la date de 282 av. J.-C., c’est-à-dire une différence de 1540 ans plus tard par la nouvelle courbe que par la formule de Newcomb.
Avec l’axe de Stone, qui est encore plus proche que celui de Lockyer du vrai, la date obtenue à partir de la formule de Newcomb est 1850 av. J.-C., mais d’après la nouvelle courbe, elle est 322 av. J.-C., c’est-à-dire 1528 ans plus tard par la nouvelle courbe que par la formule de Newcomb.
De toutes ces considérations, nous voyons très clairement que l’axe de Petrie n’est pas le véritable axe de Stonehenge, et ne peut pas donner la date astronomique correcte de sa construction.
L’axe de Lockyer : Sir Norman Lockyer, l’un des plus grands astronomes britanniques de son temps, s’intéressait profondément à Stonehenge. Son livre bien connu, Stonehenge and other British Stone Monuments Astronomically Considered, publié en 1906 (deuxième édition en 1909), donne un compte rendu complet de sa série très complète et minutieuse d’observations astronomiques à Stonehenge en juin 1901, ainsi que de beaucoup de travail qu’il a accompli pour enquêter sur d’autres anciens monuments en pierre britanniques ayant un caractère astronomique.
Ses résultats à Stonehenge ont également été publiés dans les Proceedings of the Royal Society en 1901, vol. 69, pages 137-147. MM. F.C. Penrose, F.R.S. et Howard Payn étaient associés à lui dans les observations à Stonehenge.
Il était désavantagé dans la mesure où la pierre « penchée » n° 56 du grand Trilithe central était encore dans sa position penchée et quelque peu déplacée, ce qui a nui aux observations à ce moment-là, comme cela avait déjà été fait dans le cas de la détermination de l’axe par Sir Flinders Petrie. Il a été érigé et restauré dans sa véritable position plus tard la même année 1901.
Sir Norman a reconnu que l’axe de Stonehenge devait à l’origine passer au centre du Trilithe central, car il dit
L’axe passe presque au centre à travers une inter-colonnerie (pour ainsi dire) entre les deux montants (c’est-à-dire n° 30 et 1) du cercle extérieur, et entre les montants du trilithe le plus à l’ouest tel qu’il se trouvait à l’origine.
De ce trilithe, le montant le plus méridional avec la pierre de linteau est tombé en l’an 1620, mais le compagnon a survécu comme la pierre penchée, qui a formé un objet visible et pittoresque pendant de nombreuses années, mais heureusement maintenant restaurée dans sa condition originelle de verticalité plus digne et plus sûre.
Cependant l’inclinaison de cette pierre ayant eu lieu dans la direction de l’axe de l’avenue, et comme la distance entre elle et son compagnon primitif est connue à la fois par l’analogie des deux trilithes parfaits et par la mesure des trous de mortaise sur le linteau qu’ils soutenaient autrefois, nous obtenons par bissection la mesure (c’est-à-dire 11 pouces) à partir de son bord d’un point dans la continuation de l’axe central de l’avenue et du temple et qui doit maintenant être déterminé avec beaucoup de précision.
Nous voyons d’après cette déclaration que Sir Norman Lockyer a estimé la largeur totale de l’espace entre les deux montants du Trilithe central à 22 pouces ; Mais on montrera plus loin que la distance réelle, d’après les mesures exactes, était de 36 pouces. Nous voyons aussi que Sir Norman a reconnu qu’il y avait une continuité de l’axe du cercle de Sarsen avec celui de l’avenue.
Afin de réaliser son intention de déterminer très précisément cet axe commun, il installa ensuite un « Transit Theodolite de 6 pouces par Cooke, avec des verniers indiquant à 20 » d’altitude et d’azimut », à une station « A » située sur ce qu’il croyait être l’axe, et à une distance de 61 pieds au sud-ouest du centre du cercle de Sarsen.
Cette station « A » était donc à l’extérieur du cercle de Sarsen, et à environ 10 pieds au-delà de son bord sud-ouest extérieur. De la station « A », des observations ont été faites du soleil et de l’étoile du pôle Nord (Polaris) ; et les azimuts (angles à l’est du nord) des principaux points reliés au monument ont été déterminés.
La première chose à faire était de mesurer la direction exacte de la ligne centrale de l’avenue. Dans son récit de cela, il dit
Les berges qui forment l’avenue ont subi beaucoup de dégradations. Il semble, d’après le récit de Sir Richard Colt Hoare, qu’au début du siècle dernier, on les distinguait sur une distance beaucoup plus grande qu’aujourd’hui, mais qu’ils sont encore discernables, surtout sur le côté nord, à plus de 1300 pieds du centre du temple, et en particulier sur la ligne du fond du fossé d’où la terre a été prélevée pour former la banque. et qui lui est parallèle.
Les mesures prises sur cette ligne ont aidé matériellement celles prises sur la couronne de la banque elle-même. Avec cette aide et en utilisant la rive sud et le fossé partout où il était reconnu, une estimation juste de la ligne centrale a pu être obtenue.
Pour vérifier cela, deux piquets ont été placés à des points distants de 140 pieds le long de la ligne près du début de l’avenue, et quatre autres à des distances moyennes de 100 pieds plus proches de l’extrémité la plus reconnaissable, et leurs directions ont été mesurées avec le théodolite, indépendamment par deux observateurs, le point de référence étant la flèche de Salisbury, dont le relèvement exact à partir du centre du temple avait été aimablement fourni par le colonel Johnston R.E., le Directeur général de l’Ordnance Survey.
La même chose a également été mesurée localement par les observations du Soleil et de Polaris, dont la moyenne différait de moins de 20 pouces de la valeur de l’Ordnance.
Les observations qui en ont résulté ont donné pour l’axe de l’avenue le plus proche du commencement un azimut de 49° 38' 48 », et pour celui de la partie la plus éloignée de 49° 32' 54 ».
Le milieu de ces deux lignes, tracé à partir de l’intervalle central du grand trilithe dont nous avons déjà parlé, passe entre deux des Sarsen du cercle extérieur, qui ont une ouverture d’environ 4 pieds, à quelques pouces de leur point médian, la déviation étant vers le nord.
On peut considérer que cela prouve l’étroite coïncidence de l’axe d’origine du temple avec la direction de l’avenue. Cette valeur de l’azimut, dont la moyenne est de 49° 35' 51 », est confirmée par l’information, également fournie par l’Ordnance Survey, qu’à partir du centre du temple, le repère principal de l’ancienne colline fortifiée, à environ 8 milles de distance, un campement britannique bien connu nommé Silbury ou Sidbury, est de 49° 34' 18 », et le fait que la même ligne continuait à travers Stonehenge vers le sud-ouest frappe une autre fortification ancienne, à savoir le château de Grovely, à environ 6 miles de distance et pratiquement au même azimut, à savoir 49° 35' 51".
Pour la raison ci-dessus, 49° 34' 18" a été adopté pour l’azimut de l’avenue.
Sir Norman Lockyer consigne également les azimuts, ou relèvements à l’est du nord qu’il a mesurés, de deux points importants, à savoir le sommet de la pierre du talon du Frère et le centre exact entre les pierres d’entrée 30 et 1. Il s’agit des suivants :
Point culminant du « Talon du Frère » – N 50° 39' 05 » E
Milieu de l’ouverture dans le Trilithe Nord-Est (c’est-à-dire milieu de l’ouverture entre les pierres d’entrée 30 et 1) – N 49° 42' 50"E
À partir de ces azimuts, et à partir des distances mesurées depuis la station d’observation « A » de Sir Norman, la distance exacte de l’axe de Lockyer à partir de chacun de ces points peut être calculée, à savoir :
- Distance de l’axe de Lockyer à son point le plus proche au nord-ouest du sommet de « Friar’s Heel », 6 pieds 0 pouces.
- Distance de l’axe de Lockyer : nord-ouest à partir du centre : ouverture de l’entrée entre les pierres 30 et 1 – 0 pieds 3,26 pouces (il est donc à 1 pied 8,74 pouces du côté est de la pierre d’entrée n° 30).
Au premier de ces points, le talon du moine, nous avons 5 pieds 9 pouces pour la distance correspondante de la ligne droite exactement arpentée par Stone, passant par le milieu de l’avenue et continuant à travers le cercle de Sarsen, qui constitue l’axe de Stone, que nous décrirons sous peu.
Au deuxième point, l’entrée nord-est du cercle de Sarsen, l’axe de Stone passe exactement par le point médian entre les pierres 30 et 1.
La distance entre l’axe de Lockyer et l’axe de Stone en ces deux points est donc (1) 3,0 pouces au talon du frère et (2) 3,26 pouces à l’entrée nord-est du cercle de Sarsen. Dans les deux cas, l’axe de Lockyer se trouve au nord-ouest de l’axe de Stone, c’est-à-dire sur le côté gauche regardant vers l’extérieur vers l’avenue et vers le point du lever du soleil au milieu de l’été sur Sidbury Hill.
À partir de ces deux différences axiales, et de la distance de 206 pieds, entre les deux points, on peut calculer d’autres relations entre l’axe de Lockyer et l’axe de Stone ; et la distance exacte de l’axe de Lockyer par rapport à d’autres points fixes peut également être trouvée.
Ainsi, on retrouve :
- La différence angulaire entre l’axe de Lockyer et l’axe de Stone est très faible, à savoir seulement 22" d’arc.
- L’axe de Lockyer pointe légèrement plus à l’est du nord que l’axe de Stone, et l’azimut de l’axe de Lockyer est de 49° 34' 18 » à l’est du nord, tandis que celui de l’axe de Stone est de 49° 35' 56 » à l’est du nord.
- L’axe de Lockyer croise l’axe de Stone en un point situé au centre de l’avenue, à un demi-mille au nord-est du centre du cercle de Sarsen.
- Au centre du cercle de Sarsen, l’axe de Lockyer est à 3,32 pouces de l’axe de Stone, et sur son côté nord-ouest.
- Au grand trilithe central, l’axe de Lockyer est de 3,36 pouces sur le côté nord-ouest de l’axe de Stone. À ce stade, l’axe de Stone est à 18 pouces du côté est du montant du trilithe n° 56, de sorte que l’axe de Lockyer est à 14,64 pouces du côté du n° 56.
- À l’extrémité sud-ouest de l’axe, entre la pierre n° 16 et son compagnon tombé et déplacé, le n° 15, l’axe de Lockyer est de 3,39 pouces au nord-ouest de l’axe de la pierre. L’axe de Stone, d’après sa mesure exacte, se trouve à ce point à 31 pouces du côté est du n° 16 ; par conséquent, l’axe de Lockyer est à 27,61 pouces du côté est du n° 16.
D’après l’analyse qui précède, il est clair que l’axe de Lockyer à l’intérieur du cercle de Sarsen est relié aux points fixes du cercle par les mesures suivantes
a) 3,26 pouces nord-ouest à partir du point médian entre les pierres d’entrée 30 et 1.
b) 14,64 pouces au sud-est du côté sud-est de la grande pierre du trilithe n° 56
c) 27,61 pouces au sud-est du côté sud-est de la pierre n° 16
Norman Lockyer a reconnu que la ligne centrale de l’avenue était liée de manière vitale à l’axe de Stonehenge en tant que dispositif d’observation du lever du soleil au milieu de l’été, et était essentiellement une prolongation de l’axe interne. Son axe est si proche du véritable qu’il est difficile d’arriver à une autre conclusion.
Cependant, il était désavantagé dans l’estimation de la ligne centrale de l’avenue, car, comme il le dit, les banques avaient « subi beaucoup de dégradation ». Cela explique, en partie, la différence qu’il a constatée dans les azimuts des extrémités proches et éloignées de l’axe de l’avenue : 49° 38' 48 » et 49° 32' 54 » respectivement.
Mais il y a un autre facteur dont il n’était pas conscient à l’époque. En choisissant l’emplacement de sa station « A », qui se trouvait sur sa ligne d’axe à 10 pieds au-delà du cercle de Sarsen vers le sud-ouest, à partir duquel il a fait ses divers azimuts et autres observations astronomiques, il a été influencé par la distance de l’axe, comme il l’a accepté, par rapport au montant du trilithe central, n° 56, c’est-à-dire 11 pouces. Cela a introduit une erreur de pratiquement 3 1/2 pouces, par laquelle il s’est éloigné de la vraie ligne axiale, au nord-ouest de celle-ci, à son poste d’observation « A ».
Un calcul de l’effet de ce déplacement sur les azimuts observés montre que, avec la position modifiée de la station d’observation « A », il aurait obtenu pour l’azimut de l’extrémité proche de l’axe de l’avenue 49° 35' 33 », au lieu de 49° 38' 48 », soit une réduction de 3' 15 » ; et pour l’extrémité éloignée de l’axe de l’Avenue 49° 32' 12 » au lieu de 49° 32' 54 ».
La moyenne de ces deux valeurs modifiées pour les azimuts de Lockyer des extrémités proche et éloignée de l’axe de l’avenue, à savoir 49° 33' 52 », est presque identique à celle de la ligne droite continue de Stone, représentant l’axe à la fois du cercle de Sarsen et de la ligne médiane de l’avenue, 49° 33' 54 ».
Cela confirme ainsi la croyance, exprimée plus haut dans ce chapitre, et soutenue à la fois par Sir Norman Lockyer et M. E.H. Stone, que la ligne médiane de l’avenue est le prolongement exact de l’axe original du cercle de Sarsen, et a été conçue à dessein par les constructeurs de Stonehenge pour indiquer avec précision la position du lever du soleil au milieu de l’été sur le sommet de Sidbury Hill, exactement comme ils l’ont vu lorsqu’ils ont construit le grand Cercle de Sarsen.
De plus, Sir Norman Lockyer et M. Stone se sont tous deux appuyés implicitement sur la croyance universellement acceptée des astronomes en l’exactitude des formules qu’ils utilisaient pour donner la véritable position du soleil dans les temps anciens. Pour cette raison, Sir Norman Lockyer, en utilisant la formule de Stockwell, a obtenu la date astronomique de 1680 av. J.-C. (avec une possibilité d’erreur de 200 ans, avant ou après cette date, en raison de la lenteur du taux de variation de l’obliquité de l’écliptique), comme la date la plus probable de la construction du cercle de Sarsen ; et M. Stone, en utilisant le même azimut de l’axe, 49° 34' 18 », et la formule plus récente donnée par Simon Newcomb, a obtenu la date de 1840 av. J.-C., avec une erreur possible de 200 ans dans les deux sens, de sorte qu’il dit dans son livre (page 30) « comme déterminé par des considérations astronomiques, la date de la construction de la structure actuelle de Stonehenge n’était probablement pas antérieure à environ 2040 av. J.-C., et au plus tard vers 1640 av. J.-C.
Nous voyons, d’après les résultats, que la date astronomique, trouvée en utilisant la formule de Stockwell ou de Newcomb, est très en désaccord avec les recherches archéologiques modernes décrites précédemment. Cependant, lorsque la formule est corrigée au moyen de la Nouvelle Courbe d’Obliquité, de la même manière que pour le Temple Solaire de Karnak orienté, alors la date astronomique s’accorde avec l’archéologie et l’histoire.
La méthode astronomique révisée devient donc utile dans les problèmes d’archéologie et de chronologie, lorsque les observations solaires essentielles sont disponibles.
Pour ses observations solaires à Stonehenge, Sir Norman Lockyer a mesuré l’altitude de l’horizon dans la direction de l’axe, et l’a trouvée à 35' 30". Il a supposé que l’observation du lever du soleil correspondrait au bord supérieur du soleil 2', c’est-à-dire un seizième du diamètre du soleil, et juste visible au-dessus de l’horizon. Il a adopté des corrections pour les effets combinés de réfraction et de parallaxe solaire 0° 27' 20" ; et le demi-diamètre du soleil 15' 45". En utilisant 49° 34' 18 » comme trouvé par l’Ordnance Survey pour l’azimut de l’axe de Stonehenge, et donc aussi pour l’azimut du soleil au lever du soleil au milieu de l’été à Stonehenge, et en prenant la latitude de Stonehenge comme 51° 10' 42 » Nord, il a ensuite calculé la déclinaison solstitielle du soleil, et donc l’obliquité de l’écliptique, 23° 54' 30", et donc l’époque de la construction du cercle de Sarsen de Stonehenge en 1680 av. J.-C., comme indiqué ci-dessus.
Au lieu de cela, la Nouvelle Courbe donne la date correspondant à l’axe de Newcomb 282 av. J.-C., c’est-à-dire à 68 ans de la date historique et archéologique probable, environ 350 av. J.-C.
Une différence de 68 ans, qui est faible compte tenu de la nature du problème, pourrait s’expliquer de plusieurs façons, telles que (1) une petite erreur dans l’axe supposé ; (2) le bord du soleil levant observé légèrement plus haut que les 2' supposés par Sir Norman Lockyer, disons 4' ou 5', dont le changement se produirait dans les 15 secondes suivant le premier moment d’observation ; 3° une différence de hauteur entre les arbres qui forment l’horizon lointain au sommet de Sidbury Hill, par rapport à ceux d’aujourd’hui.
Dans son livre, Stonehenge and its Date, publié en 1935, le colonel R.H. Cunnington a défini l’axe de Stonehenge, qu’il appelle « l’axe central », comme suit :
Lockyer dit que son axe passe par le centre du cercle de Sarsen, et à quelques centimètres du point central entre les pierres d’entrée 30 et 1 ; et en calculant à partir de ses données, leur distance exacte est de 3 1/2 pouces lorsque nous regardons vers l’extérieur.
L’axe central, passant par les deux points centraux, diffère donc de celui de Lockyer de 3 1/2 pouces sur 50 pieds, ce qui équivaut à 20' dans l’angle.
L’axe de Lockyer est de 49° 34', et d’après la Table des Obliquités de Newcomb, la date serait 1840 av. J.-C. (elle a été corrigée depuis que Lockyer a écrit, de sorte que la date est un peu différente). La différence de 20' équivaut à une différence de 1440 ans, de sorte que l’axe central porte la date à 400 av. J.-C. (un calcul encore plus proche donne cette date à 366 av. J.-C.)
De ce qui précède, nous voyons que l’axe de Cunninton (1) coïncide avec le centre du monument adopté par Lockyer, (2) passe au centre à travers les pierres d’entrée, et (3) a un azimut d’environ 49° 54'. Le centre de Lockyer n’était pas directement lié à une marque fixe, mais la date qu’il donne permet de la déterminer avec certitude.
Nous verrons plus loin que le centre de Lockyer ne peut pas être considéré comme le véritable centre structurel du cercle de Sarsen, mais qu’il est déplacé de 3 1/3 pouces vers l’ouest. Nous pouvons cependant définir l’axe de Cunnington par rapport aux marques fixes en notant que, en plus de passer au centre entre les pierres d’entrée 30 et 1, il passe également la pierre du talon de Friar à une distance de 4 pieds 7 pouces à l’ouest du sommet de la pierre du talon.
De plus, les calculs montrent que l’axe de Cunnington est à 12,9 pouces à l’est de la pierre du trilithe central n° 56 et à 24 1/3 pouces à l’est de la pierre n° 16. De même, on trouve que l’azimut de l’axe de Cunnington est supérieur de 0° 19' 15 » à celui de l’axe de Lockyer, et qu’il est à 49° 53' 33 » à l’est du nord, ou, comme le donne Cunnington, à 49° 54' de la minute d’arc la plus proche.
Lorsque l’axe de Cunnington est produit vers le nord-est, il diverge considérablement du centre de l’avenue et est déplacé de près de 10 pieds à droite de la ligne centrale de l’avenue à son extrémité éloignée. Cunnington était d’avis « que les lignes données par les Stones et l’Avenue divergent légèrement ».
Nous verrons cependant que l’estimation correcte de la position du centre du cercle de Sarsen et du centre du grand trilithe central met l’axe du cercle de Sarsen et la ligne centrale de l’avenue en accord exact, de sorte qu’il n’y a pas de divergence entre eux.
Le colonel Cunnington était tout à fait satisfait que les constructeurs de Stonehenge lui aient délibérément donné une orientation au lever du soleil au milieu de l’été, car, comme il le dit,
Les pierres et l’avenue suffisent à prouver au-delà de tout doute raisonnable que le monument est intentionnellement aligné au lever du soleil au milieu de l’été, et la plupart des archéologues se contentent de s’arrêter à cela ; Mais il est possible d’aller beaucoup plus loin ; mais sur un terrain beaucoup moins certain.
Il est au moins possible que l’alignement ait été fait avec une grande précision et, si c’est le cas, et si nous pouvions dire exactement ce que c’était, il serait possible de dater le monument astronomiquement.
Il y avait un objet pratique qu’un tel alignement pouvait servir, et on ne se rend pas toujours compte de l’importance que cela a pu être.
Il décrit ensuite l’utilisation probable faite de Stonehenge pour corriger l’ancien calendrier, et continue,
Ce n’est qu’après que Norman Lockyer l’eut pris en main que cet aspect de la question fut correctement traité, et son livre fit pendant un certain temps une sensation considérable.
Par la suite, cependant, les découvertes archéologiques de Stonehenge ont montré que la date astronomique de Lockyer était gravement erronée, et le colonel Cunnington commente que « de nos jours, tout le sujet de l’orientation est devenu désagréable pour les archéologues ; et c’est peut-être la raison pour laquelle certains préfèrent penser que Stonehenge n’a rien à voir avec le lever du soleil du solstice d’été, et que son orientation est le fruit de l’imagination.
Le colonel Cunnington, cependant, n’était nullement de cet avis ; mais, en utilisant le centre supposé par Lockyer du cercle de Sarsen, et en rectifiant l’axe pour passer au centre à travers l’espace entre les pierres d’entrée 30 et 1, il trouva ainsi qu’avec ce nouvel axe, et s’appuyant sur la formule de Newcomb pour donner la date astronomique correcte, la date ainsi trouvée s’accordait avec sa propre date archéologique bien fondée.
Il va maintenant être montré que l’axe de Cunnington n’est pas le véritable axe structurel du cercle de Sarsen, et ne peut pas être la ligne pointant à l’origine vers le lever du soleil au milieu de l’été. Nous voyons donc que la formule de Newcomb ne donne la bonne date archéologique que lorsqu’elle est associée à une erreur compensatoire dans l’axe supposé.
Inversement, si l’on utilise le véritable axe structurel, alors, afin d’obtenir la bonne date astronomique de construction, la formule de Newcomb elle-même doit être corrigée d’un certain facteur, et c’est le facteur donné par la nouvelle courbe pour la date en question.
On peut suggérer ici qu’un contrôle supplémentaire du centre du cercle de Sarsen pourrait être trouvé par des mesures basées sur la géométrie des « Quatre Stations », précédemment décrites ; et il semble raisonnable de croire que de telles mesures confirmeraient le centre qui va être décrit en relation avec l’axe de Stone.
À partir de l’azimut de l’axe de Cunnington, 49° 53' 33 » à l’est du nord, la déclinaison solstitielle calculée du Soleil, ou l’obliquité de l’écliptique, est de 23° 44' 25 ». D’après cela, avec la formule de Newcomb, la date astronomique correspondante calculée pour la construction de Stonehenge est 366 av. J.-C., comme indiqué précédemment. Avec la Nouvelle Courbe, la date est 436 après J.-C. Cette date est, bien sûr, tout à fait inacceptable, mais, comme dans le cas de l’axe de Petrie, la faute ne réside pas dans la Nouvelle Courbe, mais dans l’erreur de la direction dans laquelle pointe l’axe de Cunnington, 49° 53' 33" à l’est du nord.
Au lieu de cela, nous verrons maintenant que l’azimut de l’Ordnance Survey, 49° 34' 18" à l’est du nord, depuis le centre du cercle de Sarsen jusqu’au sommet de Sidbury Hill, correspond réellement, comme Sir Norman Lockyer l’a compris, à la direction réelle du lever du soleil au milieu de l’été, telle qu’elle était vue de Stonehenge lorsque le cercle de Sarsen et l’avenue ont été construits.
L’AXE DE STONE : M. E.H. Stone, membre de l’Institution of Civil Engineers et de l’American Society of Civil Engineers, a fait un levé minutieux, en juin 1923, de la ligne médiane de l’avenue et de son prolongement à travers le cercle de Sarsen. Il a décrit ce travail dans son livre The Stones of Stonehenge, publié en 1924. M. Stone définit l’axe de Stonehenge comme suit :
L’axe de la structure principale de Stonehenge telle qu’érigée par les constructeurs est la ligne passant à mi-chemin entre les pierres 56 et 55 du Trilithe central, et à mi-chemin entre les pierres 30 et 1 du cercle extérieur. Il est évident que le terme « Axe de Stonehenge » n’aurait aucun sens lorsqu’il serait appliqué à une autre ligne. (p. 131)
Dans une partie antérieure de son livre, p. 20, il indique également que nous devrions nous attendre à trouver l’Axe passant à mi-chemin entre les pierres 15 et 16 du cercle extérieur. De cette paire, le n° 15 est tombé. La partie supérieure brisée avec ses deux tenons se trouve toujours à l’intérieur du cercle.
Une analyse de la largeur des pierres de Sarsen et des espaces intermédiaires sera donnée ci-dessous. Cela montre qu’il est possible de faire une estimation précise de la largeur originale de l’espace entre 16 et 15, et que l’axe de Stone, selon toute probabilité, passe au centre de l’ouverture originale entre ces pierres.
L’arpentage de l’avenue par M. Stone et de la continuation de sa ligne médiane à travers le monument a le droit d’être considéré avec confiance en raison de ses qualifications d’ingénieur et d’arpenteur. Voici ce qu’il déclare de ces résultats :
En juin 1923, l’auteur a effectué des mesures sur l’avenue en vue de déterminer la direction de cette ligne médiane par rapport à l’axe de Stonehenge. Ces mesures ont été prises là où la position des berges et des fossés est mieux définie qu’ailleurs – sur une longueur d’environ 750 pieds, s’étendant d’environ 540 pieds à environ 1290 pieds du centre de la structure.
On sait que les fossés réels tels qu’ils ont été creusés à l’origine dans la craie sont en forme de V, et un certain nombre de sondages, avec une barre d’acier, ont été effectués par le colonel Hawley à intervalles réguliers, par lesquels les positions successives du fond du V pour chaque fossé ont été approximativement déterminées. Les points le long de l’axe de chaque fossé ainsi déterminé ont été tracés à une grande échelle, et on a constaté que, sur une longueur de 750 pieds sur laquelle les mesures ont été prises, les fossés sont pratiquement parallèles et à une distance d’environ 71 pieds de centre.
Il a été observé en outre que la ligne médiane tracée entre les deux fossés, une fois produite, passerait à peu près à mi-chemin entre les pierres d’entrée n° 1 et 30 du cercle de Stonehenge. (p. 126)
M. Stone a estimé que les résultats « justifient la conclusion que la ligne médiane de l’avenue était destinée à être un prolongement de l’axe de la structure ».
C’est pourquoi il produisit sa « ligne centrale d’arpentage ». Il a été adopté
exactement à mi-chemin entre les pierres 30 et 1 du cercle extérieur, et a été produite à travers la région de Stonehenge et de l’autre côté du cercle au-delà de la pierre n° 16.
Cette longue ligne médiane d’arpentage droite était marquée sur le sol, avec des piquets à intervalles réguliers pour une référence pratique. Au trilithe central, on a constaté que cette ligne passait à seulement 18 pouces à droite (sud-est) de la pierre n° 56. L’axe du levé occupe donc précisément la position déterminée indépendamment comme la ligne probable de l’Axe.
Cette dernière remarque se rapporte à une mesure soigneuse, faite par M. Stone, de la pierre du linteau qui se trouvait à l’origine au-dessus des pierres centrales du trilithe nos 56 et 55, et de la largeur de ces pierres, et à une estimation de la largeur de l’espace entre elles.
L’estimation de M. Stone était que l’espace original entre les numéros 56 et 55 n’était « pas moins de 2 pieds 6 pouces, et pas plus de 3 pieds 6 pouces – la moyenne étant de 3 pieds ». Nous verrons bientôt que son estimation originale de 3 pieds entre les pierres centrales du trilithe 56 et 55 est exacte, de sorte que l’Axe est passé à une distance de 18 pouces du côté oriental de la pierre debout actuelle n° 56.
On a également constaté que la longue ligne médiane de l’arpentage de M. Stone passait à une distance de 31 pouces du côté est de la pierre n° 16 de Sarsen. À la pierre de Friar’s Heel, elle se trouvait à 5 pieds 9 pouces à l’ouest du sommet de la pierre de talon.
L’axe de la pierre et le grand trilithe central
Il est important d’examiner maintenant attentivement les données disponibles sur l’espace d’origine entre les montants n° 56 et 55 du Trilithe central. La pierre n° 55 repose sur le sol, brisée en deux (c’est-à-dire avant sa restauration en 1958), la moitié supérieure reposant en partie sur la pierre de l’autel, qu’elle a manifestement poussée en biais hors de sa position lorsqu’elle est tombée. D’après les mesures effectuées sur le plan de Petrie, le Trilithon central, dans sa chute, a été incliné d’environ 6 à 8 degrés vers le nord.
Le montant ouest, n° 56, n’est pas tombé loin de la position verticale, mais s’est immobilisé contre le sommet de la pierre bleue, n° 68, devant elle, à un angle de 17 à 20 degrés par rapport à la verticale.
Le dessin de Stukeley, en 1722, le montre incliné à un angle de 20 degrés, et en 1901, lorsqu’il a été restauré, ce nombre était passé à 25 degrés, son poids lourd ayant forcé la pierre bleue, n° 68 devant elle, dans une position inclinée. Avant 1901, on avait remarqué depuis quelques années que l’inclinaison de la « pierre penchée » augmentait jusqu’à un angle dangereux.
D’autre part, le montant est, le n° 55, est tombé au sol avec une telle force qu’il a été brisé en deux morceaux. Il tomba aussi obliquement vers son compagnon, le n° 56.
La cause en était évidemment la solide fondation du n° 56 (qui était enfoncée de près de 8 pieds dans le sol) ainsi que l’effet d’accouplement de la grande pierre de linteau. Si les deux montants avaient été également libres de tomber, ils auraient conservé leur parallélisme, et l’espacement primitif entre eux aurait été conservé. Mais la contrainte exercée sur le n° 55 par son compagnon plus ferme, aidé par la pierre de linteau de liaison, fit tomber le n° 55 vers l’intérieur. Ce faisant, il s’est lourdement écrasé sur le bord supérieur de la pierre bleue n° 66, la brisant, de sorte qu’il ne restait que la souche. Il poussa également la pierre bleue centrale, le n° 67, obliquement vers le nord, et la déracina.
L’effet retardateur et pivotant de ces deux pierres bleues, ajouté au poids excessif de la pierre de linteau, a forcé la crosse du n° 55 à sortir du sol vers le haut. Cela a également fait glisser le n° 55 vers l’arrière de quatre pieds et son renversement latéral vers le n° 56.
C’était notamment une conséquence de l’accouplement du linteau. Car, comme le n° 56 cédait beaucoup moins à la perturbation, la pierre du linteau pivotait pratiquement sur le tenon du n° 56, et son autre extrémité traçait une courbe qui tirait le n° 55 vers le nord, d’une quantité qui peut être estimée géométriquement entre 1 et 2 pieds.
Un modèle du Trilithe central, et des pierres bleues 66, 67 et 68, devant lui, reproduisant les conditions de sa chute, démontre clairement ces effets, et montre comment l’espace primitif entre les montants a été réduit en position tombée. Cette conclusion est confirmée par la mesure par M. Stone de la distance entre les douilles à mortaise de la pierre de linteau, en tenant compte également de la largeur des n° 55 et 56 et de la position des tenons. M. Stone a constaté que la distance entre les trous de la douille à mortaise était de 10 pieds 6 pouces d’un centre à l’autre. Il a également soigneusement mesuré la largeur du n° 56 et a été trouvée à 7 pieds 0 1/2 pouces juste au-dessus du sol. Cette pierre est presque parfaitement droite sur son côté intérieur jusqu’à moins d’un pied du haut, où le coin est légèrement arrondi.
Le biseau est sur le côté extérieur, de sorte que la largeur du montant diminue de 7 pieds près du sol à 6 pieds près du haut. Le tenon sur le dessus de la pierre n’est « pas au milieu de la largeur de la pierre, mais à environ 3 pouces de celle-ci vers l’extérieur ». On le voit bien sur les photographies. Lorsqu’un tracé est fait du plan de Petrie de la pierre prostrée n° 55, et que les deux moitiés brisées sont assemblées, on peut voir que le bord intérieur de cette pierre, comme le n° 56, est aussi pratiquement droit d’environ un pied du niveau du sol à moins de quatre pieds du sommet, où il y a un léger biseau. augmentant à environ 8 ou 9 pouces au coin arrondi. Sur le côté extérieur, le coin supérieur est brisé à une distance de quatre pieds du haut, évidemment là où il a heurté le bord de la pierre de l’autel. La partie cassée aurait inclus le tenon, qui est manquant.
L’ouverture entre les bords intérieurs des pierres 56 et 55 du Trilithe central, depuis le niveau du sol jusqu’à quelques pieds du sommet, était pratiquement droite partout, et sa largeur peut être estimée graphiquement, conformément au schéma ci-dessous :
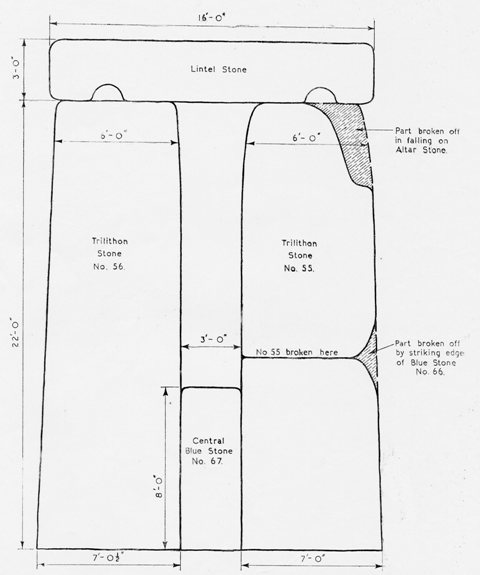
| Distance entre le centre du tenon du n° 56 et le bord intérieur droit du 56 produit vers le haut | 3 pieds, 3 pouces |
| Distance entre le tenon central du n° 55 (position probable) et le bord intérieur droit de 55 produit vers le haut | 4 pieds, 3 pouces |
|
Somme
|
7 pieds, 6 pouces |
| Distance entre le centre des trous de douille à mortaise | 10 pieds, 6 pouces |
| Différence = Largeur d’ouverture du trilithe central | 3 pieds, 0 pouces |
La pierre bleue centrale, n° 67, qui repose maintenant obliquement sur le sol, a 3 pieds de large, de sorte qu’elle couvrait à peine la largeur de l’ouverture et constituait un arrangement commode pour l’observation du lever du soleil au milieu de l’été, du point de vue d’un observateur regardant du côté sud-ouest du monument.
Le diagramme montre les dimensions originales probables du Trilithe central. Cela confirme l’exactitude de l’axe du levé de M. Stone, qui passe au centre du Trilithon, à une distance de 18 pouces du côté intérieur du montant n° 56.
Largeur de l’ouverture entre les pierres n° 16 et 15 du cercle de Sarsen
La largeur probable de cette ouverture peut être estimée comme suit :
- La pierre n° 16 est toujours debout. La pierre n° 15 a en partie disparu, mais la partie supérieure avec le tenon est couchée sur le sol, et sa largeur, mesurée sur le plan de Petrie, est de 6 pieds 3 pouces.
- La pierre n° 14 est tombée. Sa largeur près du niveau du sol d’origine est de 5 pieds 0 pouces.
- La pierre n° 13 a disparu.
- La pierre n° 12 est intacte sur le sol et a été spécialement examinée par le colonel Hawley en 1924. Il dit
Une fouille a été effectuée sur le site de la pierre n° 12 éboulée, et la zone a été agrandie plus tard pour inclure la pierre manquante n° 13. On trouva le n° 12 couché au-dessus du trou dans lequel il s’était trouvé, et il avait évidemment glissé un peu en arrière en tombant.
La position de la pierre rendait difficile le travail dans la fosse, mais on pouvait en faire assez pour avoir une vue de l’intérieur. Il était taillé nettement et avait été façonné pour prendre la pierre sans laisser d’espace sur les côtés.
La largeur de cette pierre, n° 12, est de 6 pieds 6 pouces. Nous pouvons maintenant obtenir la largeur probable de l’espace entre les pierres 16 et 15 comme suit :
| Largeur de la pierre n° 15 | 6 pieds, 3 pouces |
| Largeur de la pierre n° 14 | 5 pieds. 0 pouces |
|
Largeur présumée de la pierre n° 13 (voir ci-dessous) |
6 pieds, 5 pouces |
| Largeur totale des pierres intermédiaires nos 15, 14, 13 | 17 pieds, 8 pouces |
| Distance circulaire du côté proche de 16 au côté proche de 12, mesurée sur le plan de Petrie au milieu du cercle, correspondant à l’épaisseur moyenne des pierres | 37 pieds, 6 pouces |
| Différence = largeur totale de quatre espaces intermédiaires | 19 pieds, 10 pouces |
|
Largeur moyenne des quatre espaces
|
4 pieds, 11 1/2 pouces |
Cela confirme, avec un haut degré de probabilité, la largeur de l’espace entre les pierres 16 et 15 à l’extrémité sud-ouest de l’axe trouvé par la ligne médiane de l’arpentage de M. Stone, à savoir 5 pieds 2 pouces ; l’axe de l’arpentage étant à la moitié de cette distance, c’est-à-dire à 31 pouces du côté sud-est de la pierre n° 16. Il semble tout à fait probable que la largeur de cet espace ait pu être légèrement supérieure à celle des autres, et l’ajustement a été effectué dans une largeur diminuée de la pierre n° 13, qui aurait alors été de 6 pieds 2 1/2 pouces, soit 2 1/2 pouces de moins que la largeur moyenne des pierres de Sarsen.
Voici les largeurs générales des pierres de Sarsen au niveau du sol, et des espaces entre elles, qui peuvent être mesurées sur le plan de Petrie :
|
Numéro de
pierre
|
Largeur de la
pierre
|
Paire de
pierres
|
Largeur de
l’espace
|
|
1
|
6 pieds 10 pouces
|
30 - 1
|
4 pieds 0 pouces
|
|
2
|
7 pieds 1 pouce
|
1 - 2
|
2 pieds 9 pouces
|
|
3
|
6 pieds 3 pouces
|
2 --3
|
3 pieds 6 pouces
|
|
4
|
6 pieds 1 pouce
|
3 - 4
|
4 pieds 3 pouces
|
|
5
|
5 pieds 3 pouces
|
4 - 5
|
4 pieds 1 pouce
|
|
6
|
7 pieds 6 pouces
|
5 - 6
|
5 pieds 4 pouces
|
|
7
|
7 pieds 1 pouce
|
6 - 7
|
2 pieds 11 pouces
|
|
8
|
5 pieds 3 pouces
|
10 - 11
|
4 pieds 1 pouce
|
|
9
|
6 pieds 8 pouces
|
21 - 23
|
4 pieds 9 pouces
|
|
10
|
7 pieds 8 pouces
|
(voir note ci-dessous)
|
4 pieds 9 pouces
|
|
11
|
3 pieds 7 pouces
|
27 - 28
|
3 pieds 0 pouces
|
|
12
|
6 pieds 7 pouces
|
28 - 29
|
3 pieds 2 pouces
|
|
13
|
--
|
29 - 30
|
2 pieds 9 pouces
|
|
14
|
5 pieds 0 pouces
|
|
|
|
15
|
6 pieds 3 pouces
|
|
|
|
16
|
7 pieds 5 pouces
|
|
|
|
17
|
--
|
|
|
|
18
|
--
|
|
|
|
19
|
7 pieds 9 pouces
|
|
|
|
20
|
--
|
|
|
|
21
|
4 pieds 5 pouces
|
|
|
|
22
|
6 pieds 6 pouces
|
|
|
|
23
|
6 pieds 11 pouces
|
|
|
|
24
|
--
|
|
|
|
25
|
6 pieds 10 pouces
|
|
|
|
26
|
6 pieds 6 pouces
|
|
|
|
27
|
7 pieds 1 pouce
|
|
|
|
28
|
7 pieds 6 pouces
|
|
|
|
28
|
6 pieds 10 pouces
|
|
|
|
30
|
8 pieds 1 pouce
|
|
|
|
Largeur moyenne
|
6 pieds 5
pouces
|
Espace moyen
|
3 pieds 9,5
pouces
|
REMARQUE : Deux espaces, en tenant compte de la largeur de la pierre n° 22 tombée et déplacée (6 pieds, 6 pouces, comme indiqué ci-dessus dans la deuxième colonne)
On verra que la largeur des pierres et les espaces entre elles ne sont nullement uniformes. La pierre n° 11 était exceptionnellement étroite et n’était pas pourvue d’une pierre de linteau, peut-être, comme cela a été suggéré, pour permettre une entrée sud plus large pour les processions, avec des bannières. Les autres pierres varient d’une largeur maximale de 8 pieds 1 pouce (n° 30) à l’entrée nord-est, à 4 pieds 5 pouces (n° 21).
Certaines pierres ont été plus résistantes que d’autres en raison de divers degrés de dureté, mais la majorité des pierres sont à moins de 6 pouces de la largeur moyenne.
Le même manque d’uniformité se voit également dans les espaces entre les pierres.
(Remarque : Si nous prenons 30 fois la largeur moyenne combinée des pierres et des espaces, nous avons pour la circonférence totale du cercle, sur lequel sont situées les faces intérieures des pierres, 305 pieds 0 pouce. Le diamètre de ce cercle est de 97 pieds 1 pouce, ce qui est en bon accord avec l’opinion de Sir Flinders Petrie, mentionnée précédemment, selon laquelle les constructeurs de Stonehenge voulaient que le cercle de Sarsen ait un diamètre intérieur de 97 pieds, de sorte que le cercle lui-même serait conforme à l’ancienne norme « Year-Day Circle »).
Nous voyons que les considérations ci-dessus confirment à la fois l’exactitude des mesures de M. Stone et son affirmation selon laquelle l’axe du monument et la ligne médiane de l’avenue coïncident l’une avec l’autre.
Comme nous l’avons fait remarquer précédemment, en ce qui concerne l’axe de Lockyer, si Sir Norman Lockyer avait placé sa station d’observation « A » à seulement 3 pouces et demi à l’est de la position qu’il a adoptée, il aurait obtenu une concordance beaucoup plus étroite entre les azimuts des extrémités proches et éloignées de l’avenue. Il aurait alors trouvé la valeur moyenne modifiée, 49° 33' 58 », si proche de l’azimut de l’Ordnance Survey de la marque de référence au sommet de Sidbury Hill, 49° 34' 18 », ne différant de celle-ci que de 20 », de sorte qu’il aurait été convaincu sans aucun doute que la ligne médiane de l’avenue était le prolongement exact de l’axe de Stonehenge. Répondant vraiment à l’intention des constructeurs à cet égard.
Dans le livre de M. Stone, The Stones of Stonehenge, imprimé en 1924, aucune détermination indépendante de l’azimut de son axe de Stonehenge n’est donnée. Il accepta, pour son propre axe, l’azimut de l’Ordnance Survey de l'"Axe de Stonehenge » utilisé par Sir Norman Lockyer, à savoir 49° 34' 18 » ; et, avec une valeur ultérieure de la formule de Newcomb, il obtint une date de construction vers 1840 av. J.-C. (Stone, p. 30).
Comme l’a rapporté Sir Norman Lockyer, l’information qui lui a été fournie par l’Ordnance Survey était que « du centre du temple, le repère principal de l’ancienne colline fortifiée à environ 8 milles de distance, un campement britannique bien connu nommé Silbury ou Sidbury, est de 49° 34' 18 ».
D’après le compte rendu de Sir Norman Lockyer de ses opérations à Stonehenge, il semblerait que le colonel Johnston, R.E., le directeur général de l’Ordnance Survey, ait coopéré avec Sir Norman dans cette affaire, et a sans doute envoyé un arpenteur du département de l’Ordnance Survey pour faire les observations exactes nécessaires sur place, en les faisant à partir d’un point central choisi par Sir Norman Lockyer comme le centre le plus probable du cercle de Sarsen. aussi bien qu’il put s’en assurer.
Il a déjà été souligné que, en raison de l’élévation de la plaine intermédiaire, le repère principal, qui représente le point culminant de la colline de Sidbury (ou peut-être serait-il préférable de dire le centre approximatif de la zone formant le sommet de la colline), n’est pas facilement discernable de Stonehenge.
Cette difficulté, cependant, serait bien sûr simplement surmontée dans une telle observation de levé en utilisant un bâton de mesure élevé sur le site de la ligne de repère. Sur la ligne ainsi arpentée, et continuant à reculons au-delà de la partie sud-ouest du cercle de Sarsen, Sir Norman Lockyer fixa sa station d’observation « A » qui, dit-il, se trouvait sur sa ligne d’axe, « à une distance de 61 pieds au sud-ouest du centre du temple », et à partir de laquelle il fit des observations du soleil et de l’étoile du pôle Nord. Polaris, et en outre déterminé l’azimut des points principaux reliés au monument.
Comme il le dit, « cette ligne d’axe passait presque au centre à travers une inter-colonnerie (pour ainsi dire) entre deux montants du cercle extérieur », c’est-à-dire entre les pierres d’entrée 30 et 1. Cependant, il n’était pas exactement au centre entre eux, et, comme nous l’avons déjà vu, un calcul exact montre qu’il était de 3,26 pouces à l’ouest du centre de l’entrée.
Cette différence, aussi minime soit-elle, montre que, comme l’a souligné le colonel Cunnington, l’axe de Sir Norman Lockyer ne peut pas être le véritable axe structurel du monument ; et c’est grâce à M. Stone, par son excellent levé, que le véritable axe structurel a été localisé avec précision, et que le véritable centre structurel du cercle de Sarsen a donc dû nécessairement se trouver sur cet axe.
Il convient toutefois d’indiquer ici que, bien que le centre supposé du cercle de Sarsen par Sir Norman Lockyer ne se trouvait qu’à une très petite distance (3,32 pouces) à l’ouest du véritable centre de ce cercle, ce déplacement, sur la longue distance de 8 milles jusqu’au repère de Sidbury Hill, ne donnerait lieu qu’à une très petite différence. c’est-à-dire 1,5 pouce dans l’azimut observé de la marque de référence.
Ainsi, si l’observation du repère sur Sidbury Hill avait été faite à partir du centre de construction de Stone du cercle de Sarsen, à 3,32 pouces à l’est du centre de Lockyer, alors l’azimut du repère aurait été de 49° 34' 16,5 » au lieu de 49° 34' 18 », trouvé par l’Ordnance Survey à partir du centre de Lockyer. Cette différence est si faible qu’elle est pratiquement négligeable, car elle ne modifierait la date de construction du monument que d’environ trois ans.
Mais nous devons maintenant remarquer que les mesures du repère en tant qu’extrémité éloignée de l’axe de Stonehenge impliquent l’hypothèse que cet endroit particulier au sommet de la colline de Sidbury était le point exact du lever du soleil au milieu de l’été à la date de la construction du cercle de Sarsen.
L’axe structurel de Stonehenge, établi avec précision par M. Stone à partir de ses mesures à l’intérieur du cercle lui-même, et continuant en une seule ligne droite le long du centre de l’avenue jusqu’à la distance de 1290 pieds du centre du monument (Stone, p. 126), n’implique aucune hypothèse concernant la marque de repère sur Sidbury Hill. C’était clairement la ligne voulue par les constructeurs de Stonehenge pour indiquer par son prolongement le point du lever du soleil au milieu de l’été tel qu’ils le voyaient à la date de la construction du cercle de Sarsen.
Nous devons donc trouver l’azimut de cette droite, et bien qu’il ne soit pas donné dans le rapport de M. Stone, il peut être facilement calculé d’après les données qu’il donne, combinées avec l’azimut des points nécessaires mesuré par Sir Norman Lockyer. Ainsi, Sir Norman Lockyer donne l’azimut du centre exact entre les pierres d’entrée 30 et 1, et mesuré à partir de son poste d’observation « A », à savoir 49° 42' 50 ».
Cette station d’observation se trouvait à 3,40 pouces à l’ouest de l’axe de Stone et à une distance de 109 pieds 6 pouces, soit 1314 pouces au total, de la face intérieure des pierres d’entrée 30 et 1. Cela correspond à un angle de 0° 8' 54 », à soustraire de la mesure de Sir Norman Lockyer, 49° 42' 50 ». le résultat nous donne 49° 33' 56" comme azimut, ou direction à l’est du nord, de l’axe de Stone.
De plus, il est démontré par le calcul que l’axe de Lockyer coupe l’axe de Stone en un point au centre de l’avenue, à 2377 pieds du centre du cercle de Sarsen. La différence angulaire entre l’axe de Lockyer et l’axe de Stone (49° 34' 18 » – 49° 33' 56 ») est de 0° 0' 22 ».
L’axe de Stone est dirigé vers un point de l’horizon un peu plus à l’ouest que l’axe de Lockyer. À partir du point d’intersection des deux axes, il y a une distance d’environ 7 milles 2803 pieds, et à cette distance, la différence angulaire de 0° 0' 22" correspond à une différence de 4 pieds 3 pouces.
Puisque l’axe de Lockyer est dirigé vers le repère sur Sidbury Hill, nous trouvons donc que l’extrémité de l’axe de Stone se trouve à un point situé à 4 pieds 3 pouces à l’ouest du repère. La différence est relativement faible, et la différence angulaire à laquelle elle correspond, 0° 0' 22", représente une différence dans la date de construction, déterminée astronomiquement avec la nouvelle courbe et les tables d’obliquité, de 40 ans, à savoir de 282 av. J.-C. (axe de Lockyer) à 322 av. J.-C. (axe de Stone).
Nous voyons aussi que, tandis que la formule de Newcomb donne une date totalement inadmissible, 1822 av. J.-C., pour l’axe de Lockyer, et 1850 av. J.-C. pour l’axe de Stone, la nouvelle courbe, corrigeant la formule de Newcomb par un facteur jusque-là non reconnu, donne une date astronomique pour l’axe de Stone 322 av. J.-C., ce qui est en bon accord avec la dernière archéologie de Stonehenge. et n’est que 28 ans plus tard que la date probablement historique de la reconstruction de Stonehenge par le célèbre roi Belinus vers l’an 350 av. J.-C.
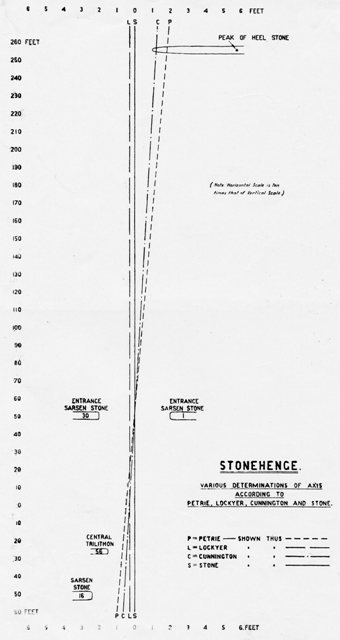
Les trilithes de Stonehenge comme moyen d’observation du lever du soleil solstitiel d’été
Comme l’a souligné le colonel Cunnington dans Stonehenge and its Date, p. 57, la hauteur au-dessus du niveau du sol de la pierre bleue centrale, n° 67, de la formation en fer à cheval en pierre bleue, était probablement de 8 pieds, la longueur totale de la pierre étant de 12 pieds ; et cela empêcherait un observateur, debout derrière le Trilithe central, de voir le point du lever du soleil au milieu de l’été à l’horizon, à moins qu’il ne se tienne sur une sorte de plate-forme.
Mais, comme le sol s’incline vers le sud-ouest à un angle d’environ 1 1/2 degré, ou 2,6 pieds sur 100 pieds, un observateur se tenant sur la ligne d’axe sur le bord intérieur de la berge, à environ 150 pieds au sud-ouest du centre du monument, aurait une vue unique du point du lever du soleil à travers les ouvertures de la pierre de Sarsen 16-15, le Trilithe central, et 30-1. (Fig. 33)
De ce point à l’intérieur de l’enceinte, et sur le bord intérieur de la berge, le champ de vision angulaire à travers les pierres sud-ouest 16-15 serait de 2° 54'. Celle-ci serait réduite au Trilithe central à 1° 22', et encore réduite, aux pierres d’entrée 30 – 1, à 1° 11'. De ce point de vue, la disposition générale des pierres de Sarsen 16 – 15 et 30 – 1, et du trilithe central, avec la pierre bleue centrale n° 67 devant elle, et avec le bord levant du soleil du milieu de l’été central dans l’image, aurait apparu comme représenté sur le diagramme ci-dessus.
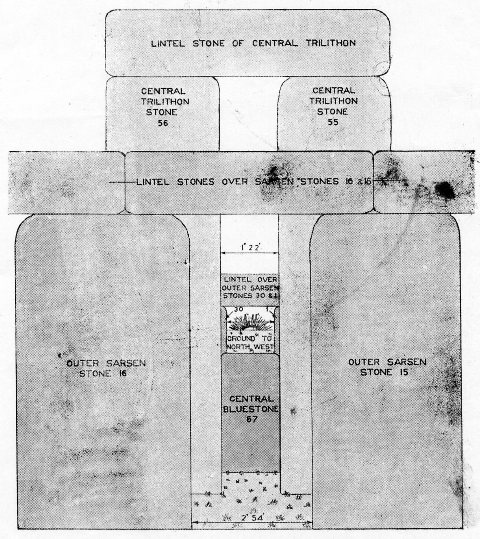
Ce cadre rectangulaire unique, formé par les grandes pierres de Sarsen et le trilithe central, était admirablement adapté à l’observation visuelle du soleil, et aurait sans aucun doute été utilisé par les anciens astronomes responsables du calendrier celtique, et aurait été d’un intérêt particulier, tout comme aujourd’hui, lorsque de nombreuses personnes se rassemblent à Stonehenge afin d’assister, d’une position convenable sur la pierre de l’autel, le soleil du milieu de l’été se levant, non pas, comme autrefois, dans la ligne centrale de l’axe le long du centre de l’avenue et au-dessus du sommet de Sidbury Hill, mais maintenant au-dessus du sommet de la pierre du talon du moine.
Avec la disposition disponible dans les temps anciens, l’observateur pouvait alors non seulement faire une observation précise du soleil dans sa position centrale au lever du soleil le jour du milieu de l’été, mais aussi noter son approche et son départ progressifs du tournant solstitiel, pendant une dizaine de jours avant et après le solstice, et ainsi fixer avec précision la date et l’heure du solstice d’été d’une année à l’autre. tout comme les anciens astronomes d’autres nations, notamment les anciens Chinois, l’ont fait dans leur système d’astronomie.
En plus de cette méthode d’observation à Stonehenge, il semble probable que les tournants du soleil, au lever du soleil au milieu de l’été et au coucher du soleil au milieu de l’hiver, aient également été marqués par la construction, en même temps que la construction de Stonehenge, des deux points de repère spéciaux à l’horizon, à savoir la fortification de Sidbury Hill au nord-est et celle correspondante à Grovely au sud-ouest. qui sont tous deux considérés comme du début de l’âge du fer.
Quiconque a constamment observé le mouvement quotidien du soleil, aux points de lever ou de coucher du soleil tout au long de l’année, peut apprécier l’intérêt et l’avantage des points de repère naturels ou construits, pour indiquer la position occupée par le soleil aux dates importantes de l’année solaire. Il semble donc probable que l’alignement unique illustré ait été intentionnellement fourni par les constructeurs de Stonehenge à cette fin astronomique.
Beaucoup de spéculations ont été faites concernant le but astronomique de la pierre du talon du moine, en relation avec le lever du soleil au milieu de l’été. En raison de la pente descendante du terrain à partir du centre du monument vers la pierre de talon, et au-delà, à un angle d’environ 1 1/2 degré par rapport à l’horizontale, ou d’environ 2 1/2 pieds sur 100 pieds, le sommet de la pierre de talon peut être vu au niveau de l’horizon lointain, et à une altitude de 0° 35' 30", par un observateur debout sur la pierre de l’autel.
On a supposé que peut-être le soleil a été vu de cette position, avec sa branche inférieure touchant apparemment à peine le sommet de la pierre du talon, lorsqu’il s’était élevé suffisamment haut pour l’amener dans l’azimut correct, à environ 50° 48' à l’est du nord, vu du centre de la pierre de l’autel.
Il n’en est pas ainsi, cependant, car l’altitude de la partie inférieure du soleil, avec l’effet de la réfraction et de la parallaxe compris, aurait été de 0° 49' 30" ; c’est-à-dire que l’ensemble du disque solaire serait à l’écart du sommet de la pierre du talon d’une quantité de 14', soit près de la moitié du diamètre du soleil.
Cependant, E. Duke, dans son livre Druidic Temples, p. 133, publié en 1846, a suggéré que la pierre du talon du moine était « un gnomon destiné à observer le lever du soleil le matin propice du solstice d’été ».
Edward Barclay, dans son livre Stonehenge, 1895, p. 11, y fait également référence comme une « pierre d’index... Au moyen de ce grand rocher non forgé, le temple est fixé au soleil levant au solstice d’été.
Pour examiner ces affirmations, nous devons maintenant déterminer où le bord de l’ombre projetée par la pierre du talon serait tombé lorsque le soleil était aligné avec la pierre du talon, vue du centre de la pierre de l’autel. Le calcul de ceci montre qu’à l’époque de la construction du cercle de Sarsen, vers 350 av. J.-C. selon les résultats précédents, l’altitude apparente dans le ciel de la branche supérieure du soleil (la déclinaison du soleil étant alors de 23° 54' 41" N.) lorsqu’il a atteint l’azimut de la pierre du talon du frère, telle qu’elle est vue de la pierre de l’autel, aurait été de 1° 20', y compris l’effet de la réfraction atmosphérique et de la parallaxe solaire.
Cette altitude solaire doit cependant être réduite de 3' à 1° 17', pour les observations d’ombre, car le bord de l’ombre dense projetée par la pierre de talon correspondrait à 3' du bord supérieur du soleil au-dessus du sommet de la pierre de talon, vu d’un point situé au bord de l’ombre.
La géométrie d’une section verticale de Stonehenge montre que le plan horizontal, sur lequel ce bord d’ombre tomberait, à proximité de la pierre de l’autel, serait à 2 pieds au-dessus du niveau de surface de la pierre de l’autel. l’ombre réelle du sommet de la pierre du Talon du Frère tomberait donc sur la pierre bleue centrale, le n° 67, qui se trouvait juste en face du grand trilithe central.
La hauteur variable de cette ombre, et son mouvement, comme on le voit sur la pierre bleue centrale tôt le matin, à la date et près de la date du solstice d’été, justifieraient donc l’opinion du révérend duc Edward selon laquelle la pierre du talon du moine, la « pierre du soleil levant », « était un gnomon dans le but d’observer le lever du soleil le matin propice du solstice d’été ».
Résumé des preuves relatives à la date de construction de Stonehenge
Les preuves précédentes, dérivées de l’astronomie et de l’archéologie de Stonehenge, confirment la croyance
- premièrement, que la reconstruction de ce grand monument britannique de l’antiquité a été affectée à l’époque celtique, lorsque la religion celtique, ou druidisme, avait atteint un haut degré de suprématie en Grande-Bretagne, et probablement vers l’an 350 av. J.-C. ;
- deuxièmement, que le cercle de Sarsen et d’autres éléments importants, en particulier la longue avenue d’entrée droite, ont été intentionnellement orientés par les constructeurs de Stonehenge avec le plus grand soin et la plus grande précision vers le point du lever du soleil au milieu de l’été sur le sommet de Sidbury Hill ;
- troisièmement, que ces conditions, et cette date, ne peuvent pas être harmonisées avec la position du soleil telle qu’elle est donnée par la formule de Newcomb pour l’obliquité de l’écliptique dans ces temps anciens.
Pour cette raison, il est devenu l’opinion commune parmi les archéologues que l’orientation astronomique ne peut pas être fiable pour jeter la lumière sur la véritable date de la construction de Stonehenge.
Au contraire, cependant, la nouvelle courbe de l’obliquité donne le facteur nécessaire de correction à la formule de Newcomb, permettant de déterminer la véritable position du soleil dans les temps anciens, et elle donne ainsi une date astronomique pour Stonehenge très proche de celle indiquée par l’histoire et par l’archéologie moderne.
Par conséquent, tout comme dans le cas du Temple Solaire de Karnak, on en arrive à la conclusion que le grand monument britannique de Stonehenge confirme, d’une manière unique et remarquable, l’exactitude de la Nouvelle Courbe de l’Obliquité de l’Écliptique, qui comprend non seulement la courbe normale du mouvement séculaire de l’axe de la Terre exprimée par la Formule de Newcomb, mais aussi la courbe de récupération de l’axe après son déplacement en l’an 2345 av. J.-C., comme l’indique l’examen des observations astronomiques anciennes, médiévales et ultérieures discutées dans les chapitres précédents de ce livre.